算法原理
对线性回归的最小二乘解,涉及到求矩阵的逆 (XTX)−1 ,
1.原始的矩阵求逆的方法–Gauss Jordan消去法,使用计算机来求解时,需要开辟另一个内存,存放变化时的右矩阵 A−1 .
2.sweep算法对高斯约旦消去法的一种改进,它可以节省存储空间,不需要开辟内存单独存放右矩阵。下面使用三阶例子来说明:
(1)对于矩阵A,其扩展矩阵 [A|I]

(2)使用高斯约旦消去法,当左边的矩阵A变为单位矩阵时,右边就得到原来左边矩阵的逆矩阵。如果第1步变第1列为基向量,得
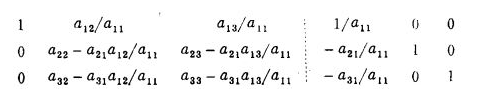
(3)当然,第1步不一定要变第1列为基向量,如果变第2列为基向量得
可以看到,不论变哪列都有如下结论:
1.当左矩阵A中的某些列未变成基向量时,右矩阵相应列的基向量形式不变。即左右两矩阵中基向量的总数恒为m,并构成一个单位矩阵。
2.左矩阵的第k列变成基向量后,右矩阵第k列才变成非基向量形式,并且该列除第k个元素为1/a(kk)外,其他元素与左矩阵的第k行相差一个符号。
由消去过程得知,当左矩阵的某些列一旦被变成基向量后,就不再起实际作用。为节省计算机的存储单元,左边单位矩阵的基向量不再存储,而把消去过程中右边刚要出现的非基向量放到做左矩阵刚变成基向量的那列位置上,并且这列元素与左矩阵的其他元素一样参加其后不运算。
其后各步消去也做类似处理,sweep变换公式:(设a(kk)不为零)
总结:对于传统的解方程问题,最原始的方法是高斯消去法,但是
sweep算法,与高斯算法相比,所需的内存缩小一半(忽略掉了一半的基向量),并且在线性回归模型中,可以顺带求出最小二乘解的误差和,用来评判模型的可靠性。
在线性回归中的应用
使用sweep算法不仅可以求逆矩阵,在线性回归模型
我们知道.如果 XTX 可逆,即 X 列满秩:
最小二乘估计








 这篇博客介绍了SWEEP算法,它是高斯约旦消去法的一种改进,节省了存储空间。在求解线性回归的最小二乘问题时,SWEEP算法不仅能够求逆矩阵,还能计算误差平方和和偏相关系数。文中还讨论了线性回归、矩阵基础知识、广义逆矩阵与线性回归的关系,以及病态设计矩阵的解决方案,如岭回归和PCA。
这篇博客介绍了SWEEP算法,它是高斯约旦消去法的一种改进,节省了存储空间。在求解线性回归的最小二乘问题时,SWEEP算法不仅能够求逆矩阵,还能计算误差平方和和偏相关系数。文中还讨论了线性回归、矩阵基础知识、广义逆矩阵与线性回归的关系,以及病态设计矩阵的解决方案,如岭回归和PCA。
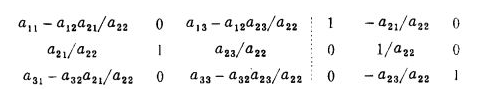
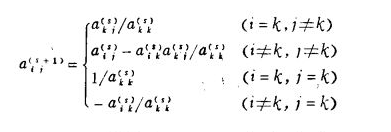
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 6175
6175

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








