3994: [SDOI2015]约数个数和
Time Limit: 20 Sec Memory Limit: 128 MBSubmit: 562 Solved: 375
[ Submit][ Status][ Discuss]
Description

Input
输入文件包含多组测试数据。
Output
T行,每行一个整数,表示你所求的答案。
Sample Input
7 4
5 6
Sample Output
121
HINT
1<=N, M<=50000
Source
题解:一道不错的数论题,很考验人的智商,很久之前就看过了,当时什么都看不懂,现在总算自己推出来了。
这道题用到了一个很神的结论
证明如下:我们知道了这个自变量的乘积拆分形式,那么如果我们枚举n的所有约数i,枚举m的所有约数j,那么i*j一定是n*m的一个约数,于是所有的i*j就包括了n*m的所有约数,那么我们只要知道有多少不同的i*j就可以了。为了知道不同的i*j,我们可以考虑如何去掉重复的i*j。这里我们考虑把i和j分为互质和不互质两种情况,设gcd(i,j)=k,于是i=p*k,j=q*k。那么i*j就可以重新组合成两个互质数的积p*k*k和q,而这两个数也分别是n和m的约数,即合法的i和j。这一点说明了一个问题:如果枚举到的i和j不互质,那么i*j这个数一定可以由另外一对互质的i’和j’表示,也就是这一对i和j是重复的;而当i和j互质的时候,p*k*k和q显然就是i和j,所以它是唯一的。于是我们总结一下上面的结论:所有i和j的积包括了n*m的所有约数,当i和j不互质时,i*j可以由另一对互质的i’和j’表示。所以我们得到所有互质的i和j的乘积就不重复地包含了n*m的所有约数,写成公式就是:d(n*m)=sigma(i|n)sigma(j|m)[(i,j)==1]。得证。
那么题目中的式子就可以进一步化简
假设N<M,
sigma(n=1..N)sigma(m=1..M) d(nm)
=sigma(n=1..N)sigma(m=1..M)sigma(i|n)sigma(j|m)[(i,j)==1]
我们改成先枚举i,j 可知i最大到N, 而j 最大到M ,i表示的是n 的约数,因sigma(n=1..N)这中间的数都要计算约数i,所有把就可以变成 sigma(i=1..N) [N/i] (这里的中括号表示下取整),j也是同理。
于是式子就变成了 sigma(i=1..N)sigma(j=1..M) [N/i][M/j] [gcd(i,j)=1]
根据[n==1]=sigma(d|n) mu[d] 就可以得到
sigma(i=1..N)sigma(j=1..M) [N/i][M/j] sigma(d|gcd(i,j)) mu[d]
sigma(i=1..N)sigma(j=1..M) [N/i][M/j] sigma(d=1..min(i,j))[d|i][d|j] mu[d]
把d 提到最前面,得到
sigma(d=1..N) sigma(i=1..[N/d])sigma(j=1..[M/d]) [N/di] [M/dj](这里是下取整) mu[d]
根据公式 [N/ab](下取整)=[[N/a]/b],进一步化简
设f(x)=sigma(i=1..x)[x/i] (下取整) 这个式子可以在o(sqrt(n))的时间内求解,一开始可以直接预处理出所有数的答案。
原式=sigma(d=1..N) f(N/d)*f(M/d) *mu[d] 因为N/d的取值都是成块分布的,所有可以预处理出mu的前缀和,
整个式子可以在o(sqrt(n))的时间内求解。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define N 50003
#define ll long long
using namespace std;
int n,m,t;
long long ans;
int prime[N],mu[N],pd[N],smu[N];
ll f[N];
void calc()
{
mu[1]=1; smu[1]=1;
for (int i=2;i<=N;i++)
{
if (!pd[i]) {
prime[++prime[0]]=i; mu[i]=-1;
}
for (int j=1;j<=prime[0];j++)
{
if (i*prime[j]>N) break;
pd[i*prime[j]]=1;
if (i%prime[j]==0)
{
mu[i*prime[j]]=0;
break;
}
else
mu[i*prime[j]]=-mu[i];
}
smu[i]=smu[i-1]+mu[i];
}
}
ll F(int x)
{
ll sum=0; int j=1;
for (int i=1;i<=x;i=j+1)
{
j=x/(x/i);
sum+=(ll)(j-i+1)*(ll)(x/i);
}
return sum;
}
int main()
{
scanf("%d",&t);
calc();
for (int i=1;i<=N;i++)
f[i]=(ll)F(i);
for (int T=1;T<=t;T++)
{
scanf("%d%d",&n,&m);
if (n>m) swap(n,m);
ll ans=0;
int j=0;
for (int i=1;i<=n;i=j+1)
{
ll a=f[n/i]; ll b=f[m/i];
j=min(n/(n/i),m/(m/i));
ans+=(ll)a*b*(smu[j]-smu[i-1]);
}
printf("%I64d\n",ans);
}
return ans;
}









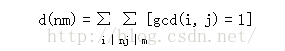













 212
212











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








