计算几何总结
一、精度控制
计算几何经常牵扯到浮点数的运算,所以就会产生精度误差,因此我们需要设置一个eps(偏差值),一般取1e-7到1e-10之间,并用下面的函数控制精度。
const double eps=1e-8;
int dcmp(double x)
{
if (fabs(x)<eps) return 0;
else return x<0?-1:1;
}有大小有方向的量,又称为矢量。
二维的向量常用一个对数(x,y)表示,代码中常用一个结构体来实现向量
struct vector
{
double x,y;
vector (double X=0,double Y=0)
{
x=X,y=Y;
}
}向量的模,即向量的长度
a=(x,y)
|a|=sqrt(x^2+y^2)
double len(vector a)
{
return sqrt(a.x*a.x+a.y*a.y)
}二维平面中的点,同样可以用对数(x,y)来表示,所以向量的存储方式同样可以用于点
typedef vector point;需要注意的是
(1)点加减向量为点
(2)点减点为向量
极角
对于向量a(x,y),可以用函数atan2(y,x)来计算他的极角
按照极角为关键字排序后的顺序为极角序
向量的四则运算
vector operator + (vector a,vector b) {return vector (a.x+b.x,a.y+b.y); }
vector operator - (vector a,vector b) {return vector (a.x-b.x,a.y-b.y);}
vector operator * (vector a,double p) {return vector (a.x*p,a.y*p);}
vector operator / (vector a.double p){return vector (a.x/p,a.y/p);}点积
a·b的几何意义为a在b上的投影长度乘以b的模长
a·b=|a||b|cosθ,其中θ为a,b之间的夹角
坐标表示
a=(x1,y1) b=(x2,y2)
a·b=x1*x2+y1*y2;
double dot(vector a,vector b)
{
return a.x*b.x+a.y*b.y;
}
点积的应用
(1)判断两个向量是否垂直 a⊥b <=> a·b=0
(2)求两个向量的夹角,点积<0为钝角,点积>0为锐角
double Angle(vector a,vector b)
{
return acos(dot(a,b)/len(a)/len(b));
}(3)求模长
double len(vector a)
{
return sqrt(dot(a,a));
}
法向量:与单位向量垂直的向量称为单位法向量
vector normal(vector a)
{
double l=len(a);
return vector (-a.y/l,a.x/l);
}
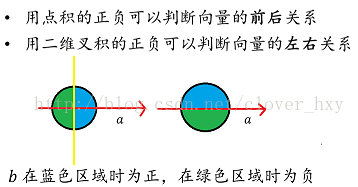
二维叉积
两个向量的叉积是一个标量,a×b的几何意义为他们所形成的平行四边形的有向面积
坐标表示a=(x1,y1) b=(x2,y2)
a×b=x1y2-x2y1
double cross(vector a,vector b)
{
return a.x*b.y-a.y*b.x;
}直观理解,假如b在a的左边,则有向面积为正,假如在右边则为负。假如b,a共线,则叉积为0,。
所以叉积可以用来判断平行。
向量的旋转
a=(x,y)可以看成是x*(1,0)+y1*(0,1)
分别旋转两个单位向量,则变成x*(cosθ,sinθ)+y1*(-sinθ,cosθ)
三、点、直线、线段的关系
点到直线的距离
利用叉积求面积,然后除以平行四边形的底边长,得到平行四边形的高即点到直线的距离
double distl(point p,point a,point b)
{
vector v=p-a; vector u=b-a;
return fabs(cross(v,u))/len(u);
}点到线段的距离
比点到直线的距离稍微复杂。因为是线段,所以如果平行四边形的高在区域之外的话就不合理,这时候需要计算点到距离较近的端点的距离
double dists(point p,point a,point b)
{
if (a==b) return len(p-a);
vector v1=b-a,v2=p-a,v3=p-b;
if (dcmp(dot(v1,v2))<0) return len(v2);
else if (dcmp(dot(v1,v3))>0) return len(v3);
return fabs(cross(v1,v2))/len(v1);
}
跨立实验:判断一条线段的两端是否在另一条线段的两侧(两个端点与另一线段的叉积乘积为负)。需要正反判断两侧。
bool segment(point a,point b,point c,point d)
{
double c1=cross(b-a,c-a),c2=cross(b-a,d-a);
double d1=cross(d-c,a-c),d2=cross(d-c,b-c);
return dcmp(c1)*dcmp(c2)<0&&dcmp(d1)*dcmp(d2)<0;
}
有两种方法,比较常用的一种是用叉积的比值计算。但是这种方法的精度不是很高。
point glt(point a,point a1,point b,point b1)
{
vector v=a1-a; vector w=b1-b;
vector u=a-b;
double t=cross(w,u)/cross(v,w);
return a+v*t;
} 还有一种比较麻烦,不常用但是精度相对较好
point line_intersection(point a,point a0,point b,point b0)
{
double a1,b1,c1,a2,b2,c2;
a1 = a.y - a0.y;
b1 = a0.x - a.x;
c1 = cross(a,a0);
a2 = b.y - b0.y;
b2 = b0.x - b.x;
c2 = cross(b,b0);
double d = a1 * b2 - a2 * b1;
return point((b1 * c2 - b2 * c1) / d,(c1 * a2 - c2 * a1) / d);
} 四、多边形相关 判断点在多边形内部
射线法:以该点为起点引一条射线,与多边形的边界相交奇数次,说明在多边形的内部。
int pointin(point p,point* a,int n)
{
int wn=0,k,d1,d2;
for (int i=1;i<=n;i++)
{
if (dcmp(dists(p,a[i],a[(i+1-1)%n+1]))==0) return -1;//判断点是否在多边形的边界上
k=dcmp(cross(a[(i+1-1)%n+1]-a[i],p-a[i]));
d1=dcmp(a[i].y-p.y);
d2=dcmp(a[(i+1-1)%n+1].y-p.y);
if (k>0&&d1<=0&&d2>0) wn++;
if (k<0&&d2<=0&&d1>0) wn--;
}
if (wn) return 1;
else return 0;
}
再多边形内取一个点进行三角剖分,用叉积求三角形的面积。因为叉积是有向面积,所以任意多边形都使用。
注意最后取绝对值。
double PolygonArea(Point* p,int n)
{
double area=0;
for(int i=1;i<n-1;i++)
area+=Cross(p[i]-p[0],p[i+1]-p[0]);
return area/2;
}
void convexhull(point *p,int n,point *ch)
{
sort(p+1,p+n+1);
if (n==1){
ch[++m]=n;
return ;
}
m=1;
for (int i=1;i<=n;i++){
while (m>2&&dcmp(cross(ch[m-1]-ch[m-2],p[i]-ch[m-2]))<=0) m--;
ch[m++]=p[i];
}
int k=m;
for (int i=n-1;i>=1;i--){
while (m>k&&dcmp(cross(ch[m-1]-ch[m-2],p[i]-ch[m-2]))<=0) m--;
ch[m++]=p[i];
}
m--;
} 六、半平面交
void cut(point a,point b)
{
point tmp[N];
int cnt=0;
for (int i=0;i<m;i++){
double c=cross(b-a,p[i]-a);
double d=cross(b-a,p[(i+1)%m]-a);
if (c<=0) tmp[cnt++]=p[i];
if (c*d<0)
tmp[cnt++]=glt(a,b,p[i],p[(i+1)%m]);
}
m=cnt;
for (int i=0;i<cnt;i++) p[i]=tmp[i];
}
求凸包上最远点对的距离
被凸包上一对平行直线卡住的点对叫做对踵点,答案一定在对踵点上。
按照逆时针顺序枚举凸包上一条边,则凸包上到该边所在直线最远的点也单调逆时针旋转,相当于用一条直线卡对面一个顶点
double rotating_calipers(point* ch,int n)//旋转卡壳,被凸包上被一对平行直线卡住的点叫对踵点,最远点对一定在凸包的一对对踵点上
{
if (n==1) return 0;
if (n==2) return dot(ch[0]-ch[1],ch[0]-ch[1]);//如果只有两个点,那么就是两点的直线距离
int now=1,i;
double ans=0;
ch[n]=ch[0];
for (int i=0;i<n;i++)
{
while(dcmp(distl(ch[now],ch[i],ch[i+1])-distl(ch[now+1],ch[i],ch[i+1]))<=0)//最远点随着平行线的旋转是单调的,所以点不会来回移动
now=(now+1)%n;
ans=max(ans,dot(ch[now]-ch[i],ch[now]-ch[i]));
ans=max(ans,dot(ch[now]-ch[i+1],ch[now]-ch[i+1]));//找到与当前直线平行的最远点,用来更新答案
}
return ans;
}
求两凸包上的最近距离
double rotating_calipers(point* p,point* q,int n,int m)//利用旋转卡壳求两个凸包上最近点的距离,一个凸包上的平行线逆时针旋转,另一个凸包上的最远点也单调逆时针旋转,所以这个算法要正反进行两遍
{
int x=0; int y=0,i;
double ans=1e10,t;
for (int i=0;i<n;i++)
x=(p[i].y<p[x].y)?i:x;
for (int i=0;i<m;i++)
y=(p[i].y>p[y].y)?i:y;
p[n]=p[0]; q[m]=q[0];
for (int i=0;i<n;i++)
{
while((t=dcmp(cross(p[x]-p[x+1],q[y+1]-q[y])))<0)//判断凸壳上下一条边的旋转方向
y=(y+1)%m;
if (t==0)//平行的时候四个点之间更新答案
{
ans=min(ans,dists(p[x],q[y+1],q[y]));
ans=min(ans,dists(p[x+1],q[y+1],q[y]));
ans=min(ans,dists(q[y],p[x],p[x+1]));
ans=min(ans,dists(q[y+1],p[x],p[x+1]));
}
else
ans=min(ans,dists(q[y],p[x],p[x+1]));//否则只用最远点更新答案
x=(x+1)%n;
}
return ans;
} 其实旋转卡壳的应用有很多变形,因为只要是凸包上满足单调性的一些问题大多都可以用旋转卡壳来解。
八、最小圆覆盖
用最小的圆覆盖平面中的所有点。
point center(point a,point b,point c){
point p=(a+b)/2; point q=(a+c)/2;
vector v=rotate(b-a,pi/2); vector u=rotate(c-a,pi/2);
if (dcmp(cross(v,u))==0) {
if(dcmp(len(a-b)+len(b-c)-len(a-c))==0)
return (a+c)/2;
if(dcmp(len(a-c)+len(b-c)-len(a-b))==0)
return (a+b)/2;
if(dcmp(len(a-b)+len(a-c)-len(b-c))==0)
return (b+c)/2;
}
return glt(p,v,q,u);
}
double mincc(point *p,int n,point &c)
{
random_shuffle(p,p+n);
c=p[0];
double r=0;
int i,j,k;
for (i=1;i<n;i++)
if (dcmp(len(c-p[i])-r)>0){
c=p[i],r=0;
for (j=0;j<i;j++)
if (dcmp(len(c-p[j])-r)>0){
c=(p[i]+p[j])/2;
r=len(c-p[i]);
for (k=0;k<j;k++)
if (dcmp(len(c-p[k])-r)>0){
c=center(p[i],p[j],p[k]);
r=len(c-p[i]);
}
}
}
return r;
} 





















 7774
7774

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








