动态规划——最优三角形

                                     动态规划——最优三角形

最近在做dp练习的时候遇到了一题需要用最优三角形算法的题，一开始完全不知道怎么解，然后去百度了一下“最优三角形”算法，看了看，好像也不是很难。就发表一下自己的理解和看法吧：

最优三角形，也就是把一个凸n多边形用不相交的对角线割成n-2个三角形，要求所割的权值最小（也就是对角线长度和最小）。然后就开始割了，首先，选定两个不相邻的点，定为V0和Vn（我把它称为原点）吧，连接V0Vn，把原多边形分成两个多边形，然后利用递归的思想一致分割，直到凸多边形完全被分割成三角形。

最后得到递归关系式：

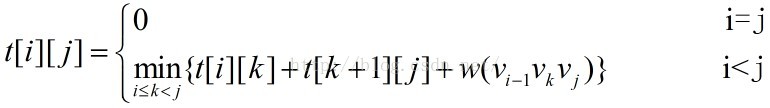
如果还是不懂的话点这里（大牛博客有详解）

另附上一题练习zoj3537