一、未登录词问题
在jieba中文分词的第一节曾提到未登录词问题
中文分词的难点
- 分词规范,词的定义还不明确 (《统计自然语言处理》宗成庆)
- 歧义切分问题,交集型切分问题,多义组合型切分歧义等
结婚的和尚未结婚的 =>
结婚/的/和/尚未/结婚/的
结婚/的/和尚/未/结婚/的 - 未登录词问题
有两种解释:一是已有的词表中没有收录的词,二是已有的训练语料中未曾出现过的词,第二种含义中未登录词又称OOV(Out of Vocabulary)。对于大规模真实文本来说,未登录词对于分词的精度的影响远超歧义切分。一些网络新词,自造词一般都属于这些词。
因此可以看到,未登录词是分词中的一个重要问题,jieba分词中对于OOV的解决方法是:采用了基于汉字成词能力的 HMM 模型,使用了 Viterbi 算法。
二、HMM
关于HMM的介绍网络上有很多资源,比如 52nlp HMM系列,在此不再具体介绍了,但一些基础知识要明确的:
HMM(Hidden Markov Model): 隐式马尔科夫模型。
HMM模型可以应用在很多领域,所以它的模型参数描述一般都比较抽象,以下篇幅针对HMM的模型参数介绍直接使用它在中文分词中的实际含义来讲:HMM解决的三类问题:
a. 评估问题(概率计算问题)
即给定观测序列 O=O1,O2,O3…Ot和模型参数λ=(A,B,π),怎样有效计算这一观测序列出现的概率.
(Forward-backward算法)
b. 解码问题(预测问题)
即给定观测序列 O=O1,O2,O3…Ot和模型参数λ=(A,B,π),怎样寻找满足这种观察序列意义上最优的隐含状态序列S。
(viterbi算法,近似算法)
c. 学习问题
即HMM的模型参数λ=(A,B,π)未知,如何求出这3个参数以使观测序列O=O1,O2,O3…Ot的概率尽可能的大.
(即用极大似然估计的方法估计参数,Baum-Welch,EM算法)- HMM 模型的五元组表示:
{
states,//状态空间
observations,//观察空间
start_probability,//状态的初始分布,即π
transition_probability,//状态的转移概率矩阵,即A
emission_probability//状态产生观察的概率,发射概率矩阵,即B
}
三、jieba HMM 分析
使用jieba对句子:”到MI京研大厦”进行分词,若是使用非HMM模式则分词的结果为:
到/MI/京/研/大厦, 使用HMM分词则结果为:到/MI/京研/大厦。下面一段是利用上一节的程序的计算结果。
"到MI京研大厦"的前缀字典:
到 205341
到M 0
到MI 0
到MI京 0
到MI京研 0
到MI京研大 0
到MI京研大厦 0
"到MI京研大厦"的DAG:
0 : [0]
1 : [1]
2 : [2]
3 : [3]
4 : [4]
5 : [5, 6]
6 : [6]
route:
{0: (-73.28491710434629, 0), 1: (-67.60579126740393, 1), 2: (-49.69423813964871, 2), 3: (-31.78268501189349, 3), 4: (-22.663377731606147, 4), 5: (-11.256112777387571, 6), 6: (-12.298425021367148, 6), 7: (0, 0)}
到/MI/京/研/大厦
...
Loading model cost 0.696 seconds.
Prefix dict has been built succesfully.
# HMM切分结果:
到/MI/京研/大厦从句子”到MI京研大厦”对应的前缀字典可以看出“京研”并没有在字典中,但是也被Viterbi算法识别出来了,可以看出HMM的强大之处了,也正是 HMM 三大基本问题之一,即根据观察序列,求隐藏状态序列。
上一节中我们说明了HMM由五元组表示,那么这样的五元组参数在中文分词中的具体含义是:
states(状态空间) & observations(观察空间).
汉字按照BEMS四个状态来标记,分别代表 Begin End Middle 和 Single, {B:begin, M:middle, E:end, S:single}。分别代表每个状态代表的是该字在词语中的位置,B代表该字是词语中的起始字,M代表是词语中的中间字,E代表是词语中的结束字,S则代表是单字成词。
观察空间为就是所有汉字(我她…),甚至包括标点符号所组成的集合。
状态值也就是我们要求的值,在HMM模型中文分词中,我们的输入是一个句子(也就是观察值序列),输出是这个句子中每个字的状态值,用这四个状态符号依次标记输入句子中的字,可方便的得到分词方案。 如:
观察序列:我在北京
状态序列:SSBE
对于上面的状态序列,根据规则进行划分得到 S/S/BE/
对应于观察序列:我/在/北京/
分词任务就完成了。
同时我们可以注意到:
B后面只可能接(M or E),不可能接(B or E)。而M后面也只可能接(M or E),不可能接(B, S)。上文只介绍了五元组中的两元 states & observations,下文介绍剩下的三元(start_probability,transition_probability,emission_probability).
start_probability(状态的初始分布).
初始状态概率分布是最好理解的,如下
P={
'B': -0.26268660809250016,
'E': -3.14e+100,
'M': -3.14e+100,
'S': -1.4652633398537678
}
示例数值是对概率值取对数之后的结果(trick, 让概率相乘变成对数相加),其中-3.14e+100作为负无穷,也就是对应的概率值是0。它表示了一个句子的第一个字属于{B,E,M,S}这四种状态的概率,如上可以看出,E和M的概率都是0,这和实际相符合,开头的第一个字只可能是词语的首字(B),或者是单字成词(S),这部分内容对应 jieba/finalseg/prob_start.py文件,具体源码。
transition_probability(状态的转移概率矩阵)
转移概率是马尔科夫链很重要的一个知识点,马尔科夫链(一阶)最大的特点就是当前T=i时刻的状态state(i),只和T=i时刻之前的n个状态有关,即:
{state(i-1), state(i-2), … state(i - n)}
HMM模型有三个基本假设:
a. 系统在时刻t的状态只与时刻t-1处的状态相关,(也称为无后效性);
b. 状态转移概率与时间无关,(也称为齐次性或时齐性);
c. 假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其它观测及状态无关,(也称观测独立性假设)。
其中前两个假设为马尔科夫模型的假设。 模型的这几个假设能大大简化问题。
再看下transition_probability,其实就是一个嵌套的字典,数值是概率求对数后的值,示例:
P={'B': {'E': -0.510825623765990, 'M': -0.916290731874155},
'E': {'B': -0.5897149736854513, 'S': -0.8085250474669937},
'M': {'E': -0.33344856811948514, 'M': -1.2603623820268226},
'S': {'B': -0.7211965654669841, 'S': -0.6658631448798212}}
如P[‘B’][‘E’]代表的含义就是从状态B转移到状态E的概率,由P[‘B’][‘E’] = -0.510825623765990,表示状态B的下一个状态是E的概率对数是-0.510825623765990。
这部分内容对应 jieba/finalseg/prob_trans.py文件,具体源码。emission_probability(状态产生观察的概率,发射概率)
根据HMM观测独立性假设发射概率,即观察值只取决于当前状态值,也就是:
P(observed[i], states[j]) = P(states[j]) * P(observed[i]|states[j]),其中P(observed[i]|states[j])这个值就是从emission_probability中获取。
emission_probability示例如下:
P={'B': {'\u4e00': -3.6544978750449433,
'\u4e01': -8.125041941842026,
'\u4e03': -7.817392401429855,
'\u4e07': -6.3096425804013165,
...,
'S':{...},
...
}比如P[‘B’][‘\u4e00’]代表的含义就是’B’状态下观测的字为’\u4e00’(对应的汉字为’一’)的概率对数P[‘B’][‘\u4e00’] = -3.6544978750449433。
这部分内容对应 jieba/finalseg/prob_emit.py文件,具体源码。
到这里已经结合HMM模型把jieba的五元参数介绍完,这五元的关系是通过一个叫Viterbi的算法串接起来,observations序列值是Viterbi的输入,而states序列值是Viterbi的输出,输入和输出之间Viterbi算法还需要借助三个模型参数,分别是start_probability,transition_probability,emission_probability。对于未登录词(OOV)的问题,即已知观察序列S,初始状态概率prob_start,状态观察发射概率prob_emit,状态转换概率prob_trans。 求状态序列W,这是个解码问题,维特比算法可以解决。
- Viterbi 维特比算法
HMM第二个问题又称为解码问题(预测问题)即给定观测序列 O=O1,O2,O3…Ot和模型参数λ=(A,B,π),怎样寻找满足这种观察序列意义上最优的隐含状态序列S。
(viterbi算法,近似算法),同样的,暴力算法是计算所有可能性的概率,然后找出拥有最大概率值的隐藏状态序列。与问题一的暴力解决方案类似,复杂度为O(N^T)。
那应该用什么方案呢?还是动态规划!
假设观察序列为O1,O2,O3,…,Ot. 在时刻i ∈ (1,t]时,定义D为观察O1,O2,…,Oi且Si=Sk时产生该观察序列的最大概率:
其中,S1,S2,….S(i-1),在此时也已经可以得到(子问题)。
它是一个是对子问题求最大值的最优解问题。
对于解码问题,因为需要求出的是使得观察序列概率最大的隐藏状态的序列,而不是最大概率,所以,在算法计算过程中,还需要记录前一个隐藏状态的值。 jieba Viterbi 的应用
jieba中对于未登录词问题,通过__cut_DAG 函数我们可以看出这个函数前半部分用 calc 函数计算出了初步的分词,而后半部分就是就是针对上面例子中未出现在语料库的词语进行分词了。
由于基于频度打分的分词会倾向于把不能识别的词组一个字一个字地切割开,所以对这些字的合并就是识别OOV的一个方向,__cut_DAG定义了一个buf 变量收集了这些连续的单个字,最后把它们组合成字符串再交由 finalseg.cut 函数来进行下一步分词。
# 利用 viterbi算法得到句子分词的生成器
def __cut(sentence):
global emit_P
# viterbi算法得到sentence 的切分
prob, pos_list = viterbi(sentence, 'BMES', start_P, trans_P, emit_P)
begin, nexti = 0, 0
# print pos_list, sentence
for i, char in enumerate(sentence):
pos = pos_list[i]
if pos == 'B':
begin = i
elif pos == 'E':
yield sentence[begin:i + 1]
nexti = i + 1
elif pos == 'S':
yield char
nexti = i + 1
if nexti < len(sentence):
yield sentence[nexti:]对应的viterbi算法:
#状态转移矩阵,比如B状态前只可能是E或S状态
PrevStatus = {
'B':('E','S'),
'M':('M','B'),
'S':('S','E'),
'E':('B','M')
}
def viterbi(obs, states, start_p, trans_p, emit_p):
V = [{}] # 状态概率矩阵
path = {}
for y in states: # 初始化状态概率
V[0][y] = start_p[y] + emit_p[y].get(obs[0], MIN_FLOAT)
path[y] = [y] # 记录路径
for t in xrange(1, len(obs)):
V.append({})
newpath = {}
for y in states:
em_p = emit_p[y].get(obs[t], MIN_FLOAT)
# t时刻状态为y的最大概率(从t-1时刻中选择到达时刻t且状态为y的状态y0)
(prob, state) = max([(V[t - 1][y0] + trans_p[y0].get(y, MIN_FLOAT) + em_p, y0) for y0 in PrevStatus[y]])
V[t][y] = prob
newpath[y] = path[state] + [y] # 只保存概率最大的一种路径
path = newpath
# 求出最后一个字哪一种状态的对应概率最大,最后一个字只可能是两种情况:E(结尾)和S(独立词)
(prob, state) = max((V[len(obs) - 1][y], y) for y in 'ES')其实到这里思路很明确了,给定训练好的模型(如HMM)参数(λ=(A,B,π)), 然后对模型进行载入,再运行一遍Viterbi算法,就可以找出每个字对应的状态(B, M, E, S),这样就可以根据状态也就可以对句子进行分词。具体源码注释见:
github/init.py 。








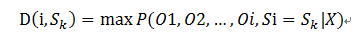
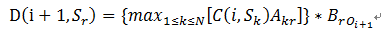














 710
710

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








