范式Huffman编码的设计与实现
摘要:
传统的 Huffman 编码需要构建 Huffman 树方可生成,但也由于树的数据结构特点,生成编码的效率不高、结构较复杂、而且在的有点程序设计语言中树也不容易实现。本文介绍不依赖于树的范式 Huffman 编码的设计与实现。使用数组求到Huffman 码的长度,再使用范式Huffman编码的原理生成前缀码。
关键字:范式Huffman编码 二叉树 模拟Huffman
引言:
现在现在多媒体技术被广泛运用于我们的日常生活这中。而压缩技术也正是多媒体技术的核心。同时压缩技术也被广泛的运用于现在通信技术。Huffman压缩算法做为压缩算法家族中重要一员,也随处可见,在如JPEG、WINRAR等标准与软件中也占有一席之地。
传统的Huffman 编码依赖于二叉树,一方面Huffman编码生成的速度不够快,另一方面在没有指针的程序设计语言中要实现二叉树结构又非常复杂。本文介绍的使用范式 Huffmann 编码和数组模拟的方法来讨论 Huffman 编码,可以提高 Huffman 较好的解决这两方面的问题。
1 基本思路
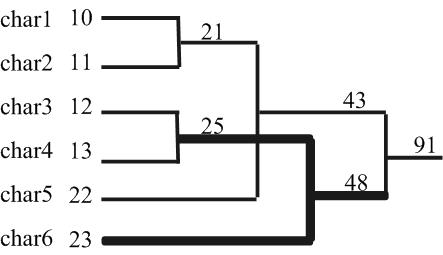
范式 Huffman 编码(Canonical Huffman Code)的基本思路是:并非只有使用二叉树建立的前缀编码才是 Huffman 编码,只要符合(1)是前缀编码(2)某一字符编码长度和使用二叉树建立的该字符的编码长度相同这两个条件的编码都可以叫做 Huffman 编码。考虑对下面六个单词的编码(Huffman树结构略):[1] Char1,char2,char3,char4,char5,char6,它们的频度分别为10,11,12,13,22,23。
| 符号 | 出现次数 | 传统 Huffman 编码 | 范式 Huffman 编码 |
Char1 | 10 | 000 | 000 |
Char2 | 11 | 001 | 001 |
Char3
| 12 | 100 | 010 |
Char4 | 13 | 101 | 011 |
Char5 | 22 | 01 | 10 |
Char6 | 23 | 11 | 11 |
构造范式Huffman编码的方法大致是:
1) 统计每个需要编码的字符的频率。
2) 根据这些频率信息求出该符号在传统Huffman编码树中的深度(也就是表示该符号所需要的位数——编码长度)。因为我们在关心的仅仅是该符号在树中的深度,完全可以放弃构造二叉树.
3) 分别统计从最大编码长度Maxlength到1的每个长度对应了多少个符号。根据这个信息从Maxlength个0 开始以递增顺序为每个符号分配编码。
4) 编码、输出压缩信息,并保存按频率顺序排列的符号表,然后保存每组同样长度编码中的最前一个编码以及该组中的编码个数。
2 算法设计:
2.1 用数组求编码在树中的深度
回顾一下Huffman树的生成过程:
1) 将字符排序。
2) 总是在排好序的字符中选出两个频度最小的字符,将频度相加。
3) 如果数大于1,重复1)-2)。
那么不用二叉树,我们同样可以使用数组来模拟这个过程。这里,我们以上表为例,它的哈夫曼二叉树如图一,下面我们来模拟这个过程,来求这个深度。
初始化:将每个一字符作放入候选式组中。每个子树都有一个子树号,但是每一个原子结点(如char1,char2等)的子树组号为0。还有一个数组用来保存每一个字符在生成的二叉树中的深度。
模拟过程:
1) 将字符按频度排序。
2) 在所有的候选子树中选择两个频度最小的子树(nod1,nod2),即头两个(因为有序)。
3) 更新深度分为四种情况:
A. nod1,nod2都为原始结点,即子树组号都为0。将nod1,nod2的深度值加1,并分配一个新的未使用过的子树组号nArraryCount给nod1,nod2。
B. nod1,nod2中nod1为原始结点,nod2为非原始结点的子树(子树组号不为0),将nod1的深度值加1,并更新子树组号nArraryCount。再将子树组号等于nod2子树给号的所有结点的的深度值加1,并更新子树组号nArraryCount。
C. nod1,nod2中nod1为非原始结点的子树,nod2为原始结点(子树组号不为0),方法类似于B。
D. nod1,nod2都为非原始结点的子树(子树组号不为0),再将子树组号等于nod2或等于nod2子树组号的所有结点的的深度值加1,并更新子树组号nArraryCount。
4) 生成一个新子树结点,频度为nod1,nod的频度值之和,组号为nArrayCount。从候选组中去掉nod1,nod2,并插入生成的新结点。
5) 若候选组中只有一个结点,则模拟过程结束。否则执行步骤1)。
上面得到的字符的深度即为字符编码的长度。
2.2 编码生成
Char1,char2,char3,char4,char5,char6的深度为3,3,3,3,2,2,所以char1 的编码为0,长度为3;char2的编码为 char1的编码加1,再右移char1长度减char2长度位,即001;同理char3,char4的编码为010,011;到char5时为1000右移3(char4的长度)减去2(char5的长度),即10;char6则为11。
3 程序设计:
程序我们设计为对一个文件的八位二进制生成Huffman编码。0x0000~0xFFFF。字符的统计程序设计比较简单本文将其略去。
模拟过程中需要使用的结构:
struct sim_Node{ //记录结点的结构
int index;
long frequency;
int row;
//让sim_NODE可以以frequency的大小排序
bool operator<(const sim_Node &x){
return frequency<x.frequency;}
};
struct sim_DEPTH{ //记录深度的结构
int row;
int depth;
};
struct HFM_Dic{
int data;
int length;
int code;
bool operator<(HFM_Dic x){
return length < x.length;
}
};
3.1 求编码在树中的深度:
HFM_Dic m_DicArray[S_LEN]; //S_LEN = 2^8=256字符总数
Void simulate()
{
list<sim_Node> lst_Nodes(S_LEN); //模拟获得深度是所用的结点
vector<sim_DEPTH> vDepths(S_LEN);
//初始化lst_Nodes,vDepths
list<sim_Node>::iterator itr=lst_Nodes.begin(),ritr=lst_Nodes.end();
int i=0;
while(itr!=lst_Nodes.end() ){
itr->index=i; //index从0开始增加
itr->row=0;
itr->frequency=m_nFreqArray[i]; //初始化统计频率
vDepths[i].depth=0;
vDepths[i].row=0;
++i, ++itr;
}
int i_row=1; //组号
while(lst_Nodes.size()>1) {
sim_Node node_Temp1,node_Temp2;
lst_Nodes.sort(); //排序新的结点表
//取出两个频率最小的结点
node_Temp1=lst_Nodes.front();
lst_Nodes.pop_front();
node_Temp2=lst_Nodes.front();
lst_Nodes.pop_front();
//结点的4种
if(0==node_Temp1.row && 0==node_Temp2.row){ //两个都为原始结点
vDepths[node_Temp1.index].row=i_row;
vDepths[node_Temp1.index].depth++;
vDepths[node_Temp2.index].row=i_row;
vDepths[node_Temp2.index].depth++;
}
if(0!=node_Temp1.row && 0==node_Temp2.row){ //其中一个为子树
vDepths[node_Temp2.index].row=i_row;
vDepths[node_Temp2.index].depth++;
const int row_temp=node_Temp1.row;
for(i=0;i<S_LEN;++i){
if(row_temp==vDepths[i].row){
vDepths[i].row=i_row;
vDepths[i].depth++;
}
}
}
if(0==node_Temp1.row && 0!=node_Temp2.row){ //其中一个为子树
vDepths[node_Temp1.index].row=i_row;
vDepths[node_Temp1.index].depth++;
const int row_temp=node_Temp2.row;
for(i=0;i<S_LEN;++i){
if(row_temp==vDepths[i].row){
vDepths[i].row=i_row;
vDepths[i].depth++;
}
}
}
if(0!=node_Temp1.row && 0!=node_Temp2.row){ //选出的两个结点都为树,而不是原始结点
for(i=0;i<S_LEN;++i){
if(vDepths[i].row==node_Temp1.row || vDepths[i].row==node_Temp2.row){
vDepths[i].row=i_row;
vDepths[i].depth++;
}
}
}
//插入新的结点
sim_Node NewNode;
NewNode.frequency=node_Temp1.frequency+node_Temp2.frequency;
NewNode.index=-1;
NewNode.row=i_row;
lst_Nodes.push_back(NewNode);
++i_row;
}
for(i=0;i<S_LEN;++i) { //复制深度到变量存储
//m_dicArray[i].code 将在GenerateCode之后得到
m_DicArray[i].data= i;
m_DicArray[i].length=vDepths[i].depth;
}
}
3.2编码的生成
void generatecode()
{
int i;
list<HFM_Dic> lst_dic(S_LEN);
list<HFM_Dic>::iterator itrlst=lst_dic.begin();
for(i=0;i<S_LEN;i++){ //初始化
itrlst->length = m_DicArray[i].length;
itrlst->data = i;
++itrlst;
}
lst_dic.sort();
lst_dic.reverse();
int shift,last_len,ncode=0;
last_len=lst_dic.front().length; itrlst=lst_dic.begin();
while(itrlst !=lst_dic.end() ){
shift= last_len - itrlst->length;
if(shift){
ncode>>=shift;
}
itrlst->code=ncode++;
last_len=itrlst->length;
++itrlst;
}
//reverse the code and copy to the m_DicArray;
itrlst=lst_dic.begin();
while(itrlst !=lst_dic.end() ){
int k,llen,newcode;
newcode=0;
llen=itrlst->length;
for(k=0; k<llen; ++k){
if( (1<<k)&itrlst->code ){
newcode |= (1<<(llen-k-1) );
}
}
}
4 结语:
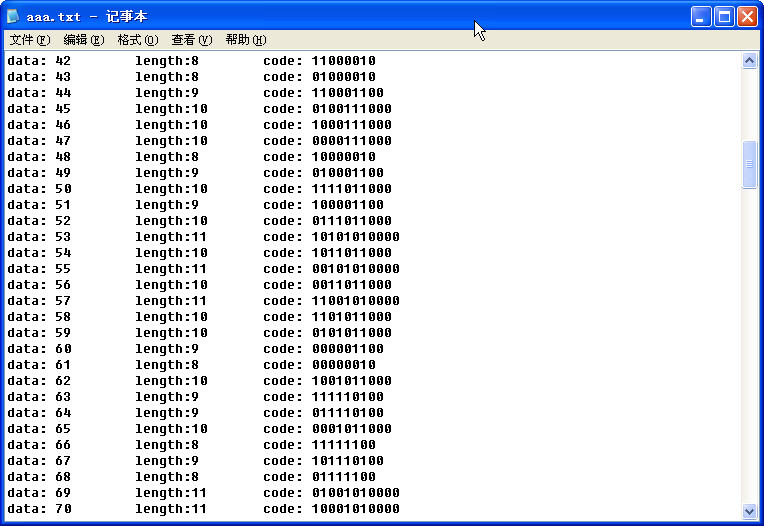
本文首先介绍了Huffman编码的传统算法,然后介绍了范式Huffman编码的算法原理,并给出了不依赖于树的范式Huffman编码的算法实现(生成的编码如右图),同时这种不依赖于树的范式Huffman编码提高了编码的生成速度,也扩大了Huffman编码的实用范围。
参考文献:
[1]王咏刚 《笨笨数据压缩教程》
[2](美)Bjarne Stroustrup 《C++程序设计语言特别版》






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








