Poj1159 Palindrome(动态规划DP求最大公共子序列LCS)

最新推荐文章于 2020-08-20 18:54:48 发布

TaiSung

最新推荐文章于 2020-08-20 18:54:48 发布

阅读量1.3k

点赞数

分类专栏： POJ 文章标签： Poj 回文 DP LCS AAA

本文链接：https://blog.csdn.net/gavin_dyson/article/details/9373099

版权

POJ 专栏收录该内容

82 篇文章 1 订阅

订阅专栏

一、Description

A palindrome is a symmetrical string, that is, a string read identically from left to right as well as from right to left. You are to write a program which, given a string, determines the minimal number of characters to be inserted into the string in order to obtain a palindrome.

As an example, by inserting 2 characters, the string "Ab3bd" can be transformed into a palindrome ("dAb3bAd" or "Adb3bdA"). However, inserting fewer than 2 characters does not produce a palindrome.

Input

Your program is to read from standard input. The first line contains one integer: the length of the input string N, 3 <= N <= 5000. The second line contains one string with length N. The string is formed from uppercase letters from 'A' to 'Z', lowercase letters from 'a' to 'z' and digits from '0' to '9'. Uppercase and lowercase letters are to be considered distinct.

Output

Your program is to write to standard output. The first line contains one integer, which is the desired minimal number.
二、题解
        这个回文问题，就是求序列X1和它的逆序列X2的最大公共子序列(LCS)长度，然后用X1的长n减去LCS长既得要添加的个数。
        现在，问题就是如何求解LCS长度了。首先，理解一下LCS的含义。（小弟刚开始的时候理解为了子串了）LCS:存在一个串S3，它的所有的串元也出现在S1和S2中，且在三个串中出现的顺序都相同，但在S1和S2中不要求连续。最长公共子序列与最长公共子串的区别在于最长公共子序列不要求在原字符串中是连续的，比如ADE和ABCDE的最长公共子序列是ADE。
        事实上，最长公共子序列问题也有最优子结构性质。然后，用动态规划的方法找到状态转换方程。

记:Xi=﹤x1，⋯，xi﹥即X序列的前i个字符 (1≤i≤m)（前缀）

Yj=﹤y1，⋯，yj﹥即Y序列的前j个字符 (1≤j≤n)（前缀）

假定Z=﹤z1，⋯，zk﹥∈LCS(X , Y)。

若xm=yn（最后一个字符相同），则不难用反证法证明：该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。
若xm≠yn，则亦不难用反证法证明：要么Z∈LCS(Xm-1, Y)，要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立，若zk≠xm则有Z∈LCS(Xm-1 , Y)，类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。

由于上述当xm≠yn的情况中，求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度，这两个问题不是相互独立的：两者都需要求LCS(Xm-1，Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS，故问题具有最优子结构性质考虑用动态规划法。

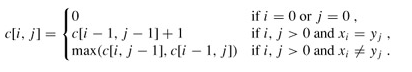
http://blog.csdn.net/v_JULY_v/article/details/6110269有详细过程

三、java代码

import java.util.Scanner; 

public class Main { 
	static int n;
	public static int LCS(String x,String y){
		short [][] z=new short [n+1][n+1];
		short i,j;
		for( i=0;i<n;i++)
			z[0][i]=0;
		for( j=1;j<n;j++)
			z[j][0]=0;
		
		for(i=1;i<=n;i++){
			for( j=1;j<=n;j++){
				if(x.charAt(i-1)==y.charAt(j-1)){
					z[i][j]=(short) (z[i-1][j-1]+1);
				}
				else
					z[i][j]=z[i-1][j] > z[i][j-1] ?z[i-1][j]:z[i][j-1];
			}
		}
		return z[n][n];
	}
    public static void main(String[] args) { 
       Scanner cin = new Scanner(System.in);
        n=cin.nextInt();
       String s=cin.next();
       String s1=new StringBuffer(s).reverse().toString();
       System.out.println(n-LCS(s,s1));
    } 
  }

/**
	 * 读取XML文件中的覆盖点信息，渲染地图
	 */
	public void readPointListInXML() {
		try {
			XmlPullParserFactory factory = XmlPullParserFactory.newInstance();
			factory.setNamespaceAware(true);
			XmlPullParser xpp = factory.newPullParser();
			xpp.setInput(
					mAppContext.getResources().getAssets().open("point_db.xml"),
					null);
			mAppContext.pointList = XmlReader.getCustomItemInfo(xpp);
		} catch (Exception e) {
		}
	}