图解机器学习总结——2、回归

一、回归的定义

回归指的是对于训练数据集$\left \{\mathbf{ x}_i,y_i \right \}$，其中，$y_i$是连续值。用过学习，找到函数$f_\theta \left ( \mathbf{ x}\right )$，使得：

$$\hat{y}_i=f_\theta \left ( \mathbf{ x}_i\right )\approx y_i$$

此时，为了度量找到的函数的优劣，设计了度量的函数，称为损失函数：

$$Loss =\frac{1}{2}\sum_{i=1}^{n}\left ( f_\theta \left ( \mathbf{ x}_i\right )-y_i \right )^2$$

二、最小二乘学习法

最小二乘法是对$Loss$函数为最小时的参数进行学习，即：

$$\hat{\theta }_{LS}=\underset{\theta }{argmin}J_{LS}\left ( \theta \right )$$

对于函数$f_\theta \left ( \mathbf{ x}\right )$，若使用线性模型，即：

$$f_\theta \left ( \mathbf{ x}\right )=\sum_{j=1}^{b}\theta _j\phi _j\left ( \mathbf{x}_i \right )=\Theta ^T\Phi \left ( \mathbf{x} \right )$$

注意：$\Theta$和$\Phi$表示的向量。

此时，损失函数的形式为：

$$J_{LS}\left ( \Theta \right )=\frac{1}{2}\left \| \Phi \Theta -\mathbf{y }\right \|^2$$

其中，$\mathbf{y }=\left ( y_1,\cdots ,y_n \right )^T$是训练输出的$n$维向量，$\Phi$是一个$n\times b$的矩阵，即：

$$\Phi =\begin{pmatrix} \phi _1\left ( \mathbf{x}_1 \right ) & \cdots & \phi _b\left ( \mathbf{x}_1 \right )\\ \vdots & \ddots & \vdots \\ \phi _1\left ( \mathbf{x}_n \right ) & \cdots & \phi _b\left ( \mathbf{x}_n \right ) \end{pmatrix}$$

为了能够求出$J_{LS}\left ( \Theta \right )$最小值时对应的参数$\Theta$：

$$\bigtriangledown _{\Theta }J_{LS}=\left ( \frac{\partial J_{LS}}{\partial \theta _1},\cdots , \frac{\partial J_{LS}}{\partial \theta _b}\right )^T=\Phi ^T\Phi \Theta -\Phi ^T\mathbf{y}$$

令其为$0$，可求得最小值时对应的参数$\Theta$：

$$\Phi ^T\Phi \Theta =\Phi ^T\mathbf{y}$$

即：

$$\Theta =\left ( \Phi ^T\Phi \right )^{-1}\Phi ^T\mathbf{y}$$

其中，$\left ( \Phi ^T\Phi \right )^{-1}\Phi ^T$与广义逆$\Phi ^\dagger$等价。

三、最小二乘法实例

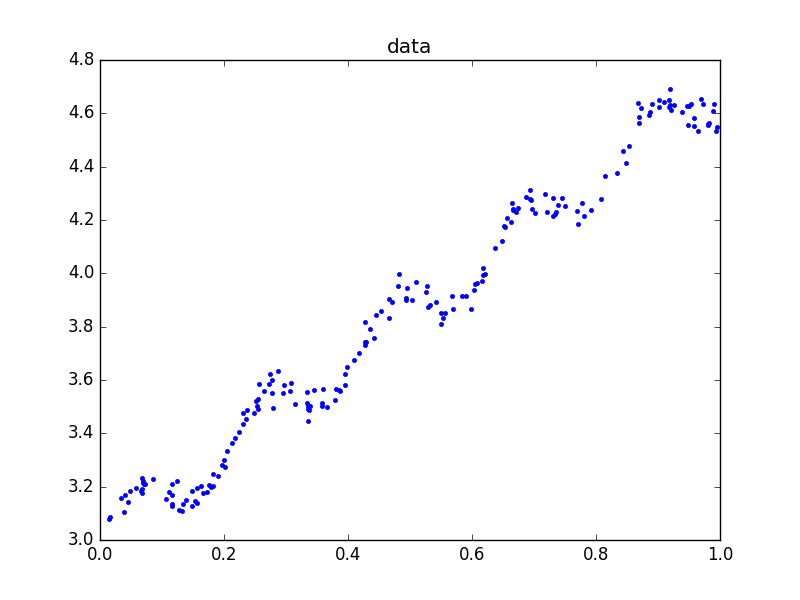
对于如下的数据集：

画图的代码如下：

#coding:UTF-8
'''
Date:20160423
@author: zhaozhiyong
'''
from pylab import *

f =open("data.txt")
x = []
y = []
for line in f.readlines():
    lines = line.strip().split("\t")
    if len(lines) == 3:
        x.append(float(lines[1]))
        y.append(float(lines[2]))
f.close()

plot(x,y,".")
plt.title("data")
show()

利用最小二乘法求得的结果为：
[[ 3.00774324]
[ 1.69532264]]

代码如下：

#coding:UTF-8
'''
Date:20160423
@author: zhaozhiyong
'''

from numpy import *

def load_data():
    f = open("data.txt")
    x = []
    y = []
    for line in f.readlines():
        lines = line.strip().split("\t")
        x_tmp = []
        if len(lines) == 3:
            x_tmp.append(float(lines[0]))
            x_tmp.append(float(lines[1]))
            y.append(float(lines[2]))
        x.append(x_tmp)
    f.close()
    return mat(x), mat(y).T

def lr(x, y):
    if linalg.det(x.T * x) != 0:
        return ((x.T * x)**(-1) * (x.T) * y)    

if __name__ == "__main__":
    x, y = load_data()
    #核心的最小二乘
    w = lr(x,y)
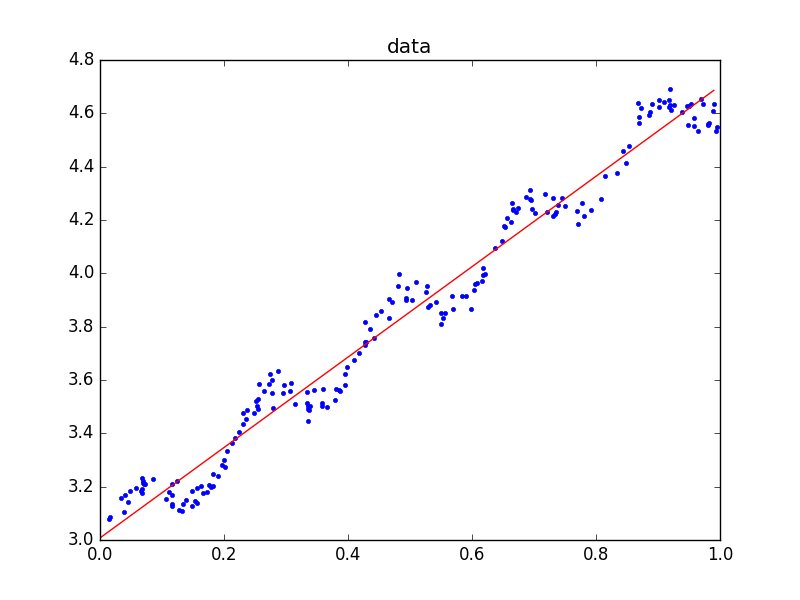
    print w

最终的图形如下：

四、局部加权线性回归

在上图中，我们发现直线并不能很好的拟合数据点，我们可以通过对数据点的局部进行加权，即：

$$Loss =\frac{1}{2}\sum_{i=1}^{n}\left ( f_\theta \left ( \mathbf{ x}_i\right )-y_i \right )^2$$

通常对于权值，可以取为高斯核函数：

$$w\left ( i,i \right )=exp(\frac{\left | x_i-x \right |}{-2k^2})$$

则此时，最优的参数$\Theta$为：

$$\Theta =\left ( \Phi ^T\mathbf{W}\Phi \right )^{-1}\Phi ^T\mathbf{W}\mathbf{y}$$

五、最小二乘的性质

对于矩阵$\Phi$，对其进行奇异值分解：

$$\Phi =\sum_{k=1}^{min\left ( n,b \right )}\kappa _k\psi _k\phi _k^T$$

其中，$\kappa _k$称为奇异值，具有非负性，$\psi _k$称为左奇异向量，$\phi _k$称为右奇异向量，对于左奇异向量和右奇异向量，其满足正交性：

$$\psi _i^T\psi _{{i}'}=\begin{cases} 1 & \text{ if } i={i}' \\ 0 & \text{ if } i\neq {i}' \end{cases}$$

$$\phi _j^T\phi _{{j}'}=\begin{cases} 1 & \text{ if } j={j}' \\ 0 & \text{ if } j\neq {j}' \end{cases}$$

此时，矩阵$\Phi$的广义逆矩阵$\Phi ^{\dagger }$可以表示为：

$$\Phi ^{\dagger } =\sum_{k=1}^{min\left ( n,b \right )}\kappa ^{\dagger }_k\psi _k\phi _k^T$$

其中：

$$\kappa ^{\dagger }=\begin{cases} \frac{1}{\kappa } & \text{ if } \kappa \neq 0\\ 0 & \text{ if } \kappa = 0 \end{cases}$$

对于训练样本的输入$\left \{ \mathbf{x}_i \right \}$，其预测值为：

$$\left ( f_{\hat{\Theta _{LS}}}\left ( \mathbf{x}_1 \right ),\cdots ,f_{\hat{\Theta _{LS}}}\left ( \mathbf{x}_n \right ) \right )^T=\Phi \hat{\Theta _{LS}}=\Phi \Phi ^{\dagger }\mathbf{y}$$

其中，$\Phi \Phi ^{\dagger }$是$\Phi$在$R\left ( \Phi \right )$上的正交投影矩阵。由此可见，最小二乘法的输出向量$\mathbf{y}$是由$R\left ( \Phi \right )$的正交投影得到的。

六、大规模数据的学习算法

对于上述的最小二乘的求解方法，需要将训练数据以矩阵的形式全部存入内容中才能进行计算，这样的方法不利于大规模的数据集，在大规模的数据集的情况下，通常使用的方法是基于梯度下降的方法，如随机梯度下降法，由于损失函数$J$是一个凸函数：

(凸函数)$J\left ( \theta \right )$是凸函数，指的是对任意的两地点$\theta _1$和$\theta _2$和任意的$t\in \left [ 0,1 \right ]$，有：

$$J\left ( t\theta _1+\left ( 1-t \right )\theta _2 \right )\leqslant tJ\left ( \theta _1 \right )+\left ( 1-t \right )J\left ( \theta _2 \right )$$

随机梯度下降法的基本步骤如下：

• 随机初始化参数$\Theta$
• 选择一个样本$\left (\mathbf{ x}_i,y_i \right )$，对参数$\Theta$进行更新：
  $$\Theta =\Theta -\eta \triangledown J_{LS}^{\left ( i \right )}\left ( \Theta \right )$$

其中：

$$\triangledown J_{LS}^{\left ( i \right )}\left ( \Theta \right )=\Phi \left ( \mathbf{x}_i \right )\left ( f_{\Theta }\left ( \mathbf{x}_i \right )-y_i \right )$$

• 直到解达到收敛精度为止，重复上述的步骤。

对于上述的回归问题，随机梯度下降法的求解结果为：

[[ 3.02488533 1.68122429]]

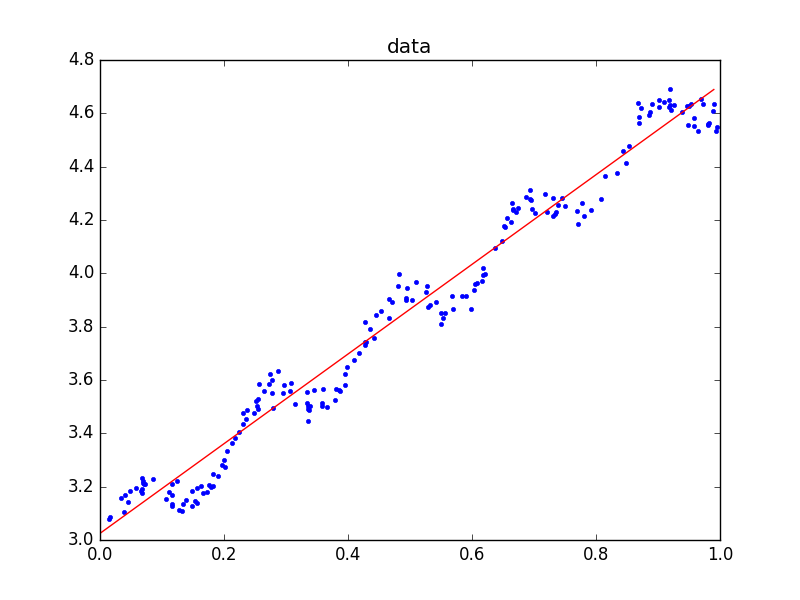
回归的结果如下：

程序代码如下：

#coding:UTF-8
'''
Date:20160423
@author: zhaozhiyong
'''

from numpy import *

def sgd(n, p):
    f = open("data.txt")
    w = mat(zeros((1, n)))#初始化
    for line in f.readlines():
        lines = line.strip().split("\t")
        x_tmp = []
        y = 0.0
        if len(lines) == 3:
            x_tmp.append(float(lines[0]))
            x_tmp.append(float(lines[1]))
            y = float(lines[2])
        x = mat(x_tmp).T
        w = w - p * (w * x - y) * x.T      
    f.close()
    return w

if __name__ == "__main__":
    w = sgd(2, 0.1)
    print w