PCA(principal component analysis)主成分分析法

《Aggregating local descriptors into a compact image representation》论文笔记
在论文中，提取到VLAD特征后，要对特征向量进行PCA降维，就是用一个大小为D’ * D的矩阵M，对VLAD特征向量x做变换，降维后的vector是x’ = Mx，x’的大小是D’维。矩阵M是由原样本的协方差矩阵的D’个特征向量构成。
为什么M要是特征向量的矩阵呢？
根据PRML中的内容，理解如下：

1，Maxinum Variance Formulation

PCA的一种定义就是要使降维后的特征点的方差尽可能大。
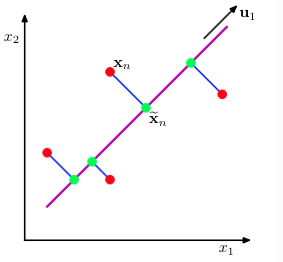
考虑如上图中二维的一组特征点x，现在要对它们降到1维，图中$u_1$是单位向量，它描述一个方向，那么每个x降维后就是$u_1^Tx$。我们希望，降维后样本尽量分散，尽可能不损失或少损失差异信息。也就是说，图中的红色点映射到$u_1$上的绿色点，要尽可能区分开，绿色点距离较近或者重合都会导致特征点差异信息损失，从而使搜索精度降低。

特征点均值：$x = \frac{1}{N} \sum_{n=1}^N x_n$，映射后均值：$u_1^T x$
映射后特征点方差(variance)：$\frac{1}{N}\sum_{n=1}^N(u_1^Tx_n - u_1^T x) ^ 2 = u_1 S u_1$
其中S是原特征点集的协方差矩阵：$S=\frac{1}{N}\sum_{n=1}^N(x_n - x)(x_n - x)^T$
我们的目标就是求一个$u_1$使得映射后特征点方差$u_1 S u_1$最大，还有一个约束条件：$u_1^T u_1 = 1$
用拉格朗日乘数法求解，写出拉格朗日函数：$L = u_1 S u_1 + \lambda_1(1 - u_1^T u_1 )$
对$u_1$求偏导并令偏导为0，可得：$Su_1 = \lambda_1 u_1，u_1 S u_1 = \lambda_1.$
可以看出，$\lambda_1$是S的一个特征值，$u_1$是它对应的一个特征向量，要使$u_1 S u_1$最大，则$\lambda_1$要取S的最大的特征值。
所以PCA方法中用来做变换的矩阵M是这样构成的：将原特征点集的协方差矩阵的特征值从大到小排列，取前D’个，把它们对应的特征向量取出来组成M，M的第1行就是$u_1$，第D’行是$u_{D'}$，这个M是一个正交矩阵。
降维后原特征点必然会损失一些信息，我们把降维后的x’再映射回去，得到$x_p$，$x_p = M^T x' = M^T M x$，那么$x_p = x + \varepsilon_p(x).$，其中$\varepsilon_p(x)$是降维造成的信息损失(projection loss)。

2，Minimum-error formulation

PCA的另一种定义是最小误差，也就是特征点在映射过程中的损失最小，使映射后的样本和映射前尽可能近似，反映在上文的图中就是要使蓝色的线段最短。

这样我们就可以得到一个新的优化问题，这个优化问题的解与最大方差得到的解是一致的。详细可见《Pattern Recognition and Machine Learning》。

---

论文中对传统的PCA方法做了改进。
比如，全特征点集的协方差矩阵的特征值从大到小排列为$\lambda_1,\lambda_2...\lambda_D$，对应的特征向量为$u_1,u_2...u_D$，我们取特征向量的前D’个构成矩阵M，用这个矩阵$M = [u_1^T, u_2^T,...,u_{D'}^T]^T$来映射样本集$X=[x_1,x_2...x_N]$，这里的$x_n$都是特征向量，我们得到映射后的样本集

$$X' = MX = \left[ \begin{matrix} u_1x_1 & ... & u_1x_N \\ ... & ... & ... \\ u_{D'}x_1 & ... & u_{D'}x_N \end{matrix} \right].$$
可以看到，在X’的前几行，是用较大的特征值对应的特征向量映射的，那么这一部分数据方差较大，而到下面几行，方差会越来越小，这样会导致在建立ADC索引时，对于X’上面几行的方差较大的子向量(subvector)，索引编码会更粗糙一些（因为在ADC中对于每组subvector都是产生固定的k个聚类中心来作为codebook），这样就容易损失数据信息，影响搜索精度，所以需要balance方差。
于是论文中引入一个Q，得到如下优化问题：
$$Q = argmin E_x[||\epsilon_q(QMX)||^2].$$
那么由PCA降维后的特征点集就是 $X'' = QX' = QMX.$
而这个优化问题难以直接求解，文中提到两种方法：
1，令矩阵Q为Householder矩阵，则Q可以分解: $Q = I - 2vv^T.$其中I是单位矩阵，v未知，这样把Q代入上述优化问题，可求得v，进而求得Q，具体求解过程论文没有提供。
2，为矩阵Q随机赋值，论文中提到，这样的Q在实验中的结果还可以。

---

3，PCA代码

function [Y, E, mu] = pca_(X) 
%[Y,V,E,D] = pca_(X)

% do PCA on image patches
%
% INPUT variables:
% X                  matrix with image patches as columns
%
% OUTPUT variables:
% Y                  the project matrix of the input data X without whiting
% V                  whitening matrix
% E                  principal component transformation (orthogonal)
% D                  variances of the principal components

%去除直流成分
mu = mean(X, 2);
X  = X-repmat(mean(X, 2), 1, size(X, 2));

% Calculate the eigenvalues and eigenvectors of the new covariance matrix.
covarianceMatrix = X*X'/(size(X,2)-1); %求出其协方差矩阵
%E是特征向量构成，它的每一列是特征向量，D是特征值构成的对角矩阵
%这些特征值和特征向量都没有经过排序
[E, D] = eig(covarianceMatrix); 

% Sort the eigenvalues  and recompute matrices
% 因为sort函数是升序排列，而需要的是降序排列，所以先取负号,diag(a)是取出a的对角元素构成
% 一个列向量，这里的dummy是降序排列后的向量，order是其排列顺序
[~,order] = sort(diag(-D));
E = E(:,order);%将特征向量按照特征值大小进行降序排列，每一列是一个特征向量
Y = E'*X;
d = diag(D); %d是一个列向量
%dsqrtinv是列向量，特征值开根号后取倒,仍然是与特征值有关的列向量
%其实就是求开根号后的逆矩阵
dsqrtinv = real(d.^(-0.5)); 
Dsqrtinv = diag(dsqrtinv(order));%是一个对角矩阵，矩阵中的元素时按降序排列好了的特征值（经过取根号倒后）
D = d(order);%D是一个对角矩阵，其对角元素由特征值从大到小构成
V = Dsqrtinv*E';%特征值矩阵乘以特征向量矩阵

E = E'; % 每一行为一个特征向量，降序排列