机器学习优化算法—L-BFGS

关于优化算法的求解，书上已经介绍了很多的方法，比如有梯度下降法，坐标下降法，牛顿法和拟牛顿法。梯度下降法是基于目标函数梯度的，算法的收敛速度是线性的，并且当问题是病态时或者问题规模较大时，收敛速度尤其慢（几乎不适用）；坐标下降法虽然不用计算目标函数的梯度，但是其收敛速度依然很慢，因此它的适用范围也有局限；牛顿法是基于目标函数的二阶导数（海森矩阵）的，其收敛速度较快，迭代次数较少，尤其是在最优值附近时，收敛速度是二次的。但牛顿法的问题在于当海森矩阵稠密时，每次迭代的计算量比较大，因为每次都会计算目标函数的海森矩阵的逆，这样一来，当问题规模较大时，不仅计算量大（有时大到不可计算），而且需要的存储空间也多，因此牛顿法在面对海量数据时由于每一步迭代的开销巨大而变得不适用；拟牛顿法是在牛顿法的基础上引入了海森矩阵的近似矩阵，避免每次迭代都要计算海森矩阵的逆，拟牛顿法的收敛速度介于梯度下降法和牛顿法之间，是超线性的。拟牛顿法的问题也是当问题规模很大时，近似矩阵变得很稠密，在计算和存储上也有很大的开销，因此变得不实用。

另外需要注意的是，牛顿法在每次迭代时不能总是保证海森矩阵是正定的，一旦海森矩阵不是正定的，优化方向就会“跑偏”，从而使得牛顿法失效，也说明了牛顿法的鲁棒性较差。拟牛顿法用海森矩阵的逆矩阵来替代海森矩阵，虽然每次迭代不能保证是最优的优化方向，但是近似矩阵始终是正定的，因此算法总是朝着最优值的方向在搜索。

从上面的描述可以看出，很多优化算法在理论上有很好的结果，并且当优化问题的规模较小时，上面的任何算法都能够很好地解决问题。而在实际工程中，很多算法却失效了。比如说，在实际工程中，很多问题是病态的，这样一来，基于梯度的方法肯定会失效，即便迭代上千上万次也未必收敛到很好的结果；另外，当数据量大的时候，牛顿法和拟牛顿法需要保存矩阵的内存开销和计算矩阵的开销都很大，因此也会变得不适用。

本文将介绍一种在实际工程中解决大规模优化问题时必然会用到的优化算法：L-BFGS算法。

上面已经提到了在面对大规模优化问题时，由于近似矩阵往往是稠密的，在计算和存储上都是n²的增长，因此拟牛顿法变得不适用。

L-BFGS算法就是对拟牛顿算法的一个改进。它的名字已经告诉我们它是基于拟牛顿法BFGS算法的改进。L-BFGS算法的基本思想是：算法只保存并利用最近m次迭代的曲率信息来构造海森矩阵的近似矩阵。

在介绍L-BFGS算法之前，我们先来简单回顾下BFGS算法。

在算法的每一步迭代，有如下式：

，      k = 0, 1, 2,…,           （1）

式（1）中a_k是步长，H_k的更新通过如下公式：

 （2）

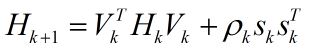
在式（2）中

 （3）

 （4）

 （5）

（6）

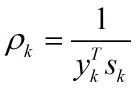
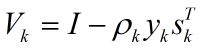
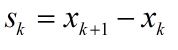
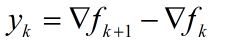
从式（2）到式（6）可以看出H_k+1是用{s_k, y_k}修正H_k来得到的。需要注意的是，这里H_k表示海森矩阵的逆的近似矩阵。

在BFGS算法中，由于H_k随着迭代次数的增加会越来越稠密，当优化问题的规模很大时，存储和计算矩阵H_k将变得不可行。

为了解决上述问题，我们可以不存储矩阵H_k，而是存储最近m次迭代的曲率信息，即{s_k, y_k}。每当完成一次迭代，最旧的曲率信息{s_i, y_i}将被删除，而最新的曲率信息被保存下来。通过这种方式，算法保证了保存的曲率信息是来自于最近的m次迭代。在实际工程中，m取3到20往往能有很好的结果。除了更新矩阵H_k的策略和初始化H_k的方式不同外，L-BFGS算法和BFGS算法是一样的。

下面将会详细介绍一下矩阵H_k的更新步骤。

在第k次迭代，算法求得了x_k，并且保存的曲率信息为{s_i, y_i}，其中i = k-m, …, k-1。为了得到H_k，算法首先选择一个初始的矩阵H_k⁰，这是不同于BFGS算法的一个地方，L-BFGS算法允许每次迭代选取一个初始的矩阵，然后用最近的m次曲率信息对该初始矩阵进行修正，从而得到H_k。

通过反复利用式（2），我们可以得到下式：

     （7）

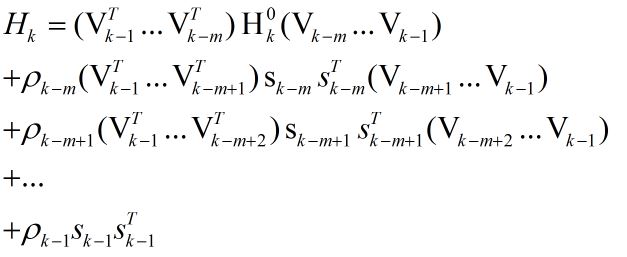
关于每次迭代时H_k⁰的初始值的设定，一个在实践中经常用到的有效方法为：

 （8）

（9）

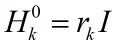
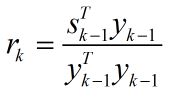
其中r_k表示比例系数，它利用最近一次的曲率信息来估计真实海森矩阵的大小，这就使得当前步的搜索方向较为理想，而不至于跑得“太偏”，从而使得步长a_k = 1在大多数时候都是满足的，这样就省去了步长搜索的步骤，节省了时间。

在L-BFGS算法中，通过保存最近m次的曲率信息来更新近似矩阵的这种方法在实践中是很有效的。

虽然L-BFGS算法是线性收敛，但是每次迭代的开销非常小，因此L-BFGS算法执行速度还是很快的，而且由于每一步迭代都能保证近似矩阵的正定，因此算法的鲁棒性还是很强的。

百度最近提出了一个shooting算法，该算法比L-BFGS快了十倍。由于L-BFGS算法的迭代方向不是最优的，所以我猜想shooting算法应该是在迭代的方向上做了优化。