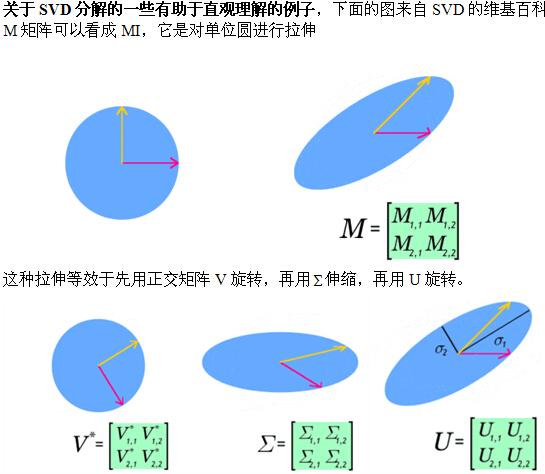
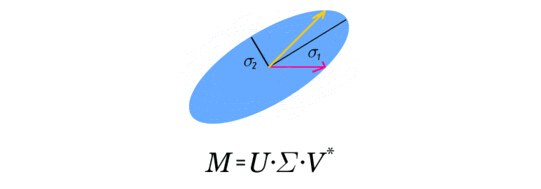
引子:SVD分解就是把一个实数矩阵M分拆成UDV。U,V都是正交旋转矩阵。这个分拆可以形象的理解为,我要看看这个空间M性质怎么样?那我可以用标准笛卡尔空间来构造出一个一模一样的M空间。想象M空间是个特殊形状的泥塑,笛卡尔空间是块标准的正方形泥块。把笛卡尔空间放在手里,先旋转着看看(即左乘V),再找合适的地方捏捏它(再左乘D),好让它和M一样。最后再旋转(再左乘U),把它摆得和M一样。这样就360度无死角的构造了一个M空间。如果发现M空间有的地方很扁,那么我就掉丢这个维度,这就是SVD的降维,也是SVD的核心。
注释:关于上面为何是特征向量的说明。
PS:一室友秦屌,问我M不是方阵,是3*2的矩阵。作用在2*1的向量 x 上,Mx 就变成了三维的了。这还能通过两次旋转达到效果吗?注意,旋转也可以是不同维度的,不只是在平面内旋转。一个正方形我可以让它绕着原点立起来旋转。这就由二维变成三维了。
reference:
http://www.ams.org/samplings/feature-column/fcarc-svd
http://en.wikipedia.org/wiki/Singular_value_decomposition#History
http://diaorui.net/archives/61











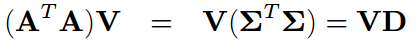














 7329
7329











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








