转载请声明出处http://blog.csdn.net/zhongkejingwang/article/details/43083603
前面文章SVD原理及推导已经把SVD的过程讲的很清楚了,本文介绍如何将SVD应用于推荐系统中的评分预测问题。其实也就是复现Koren在NetFlix大赛中的使用到的SVD算法以及其扩展出的RSVD、SVD++。
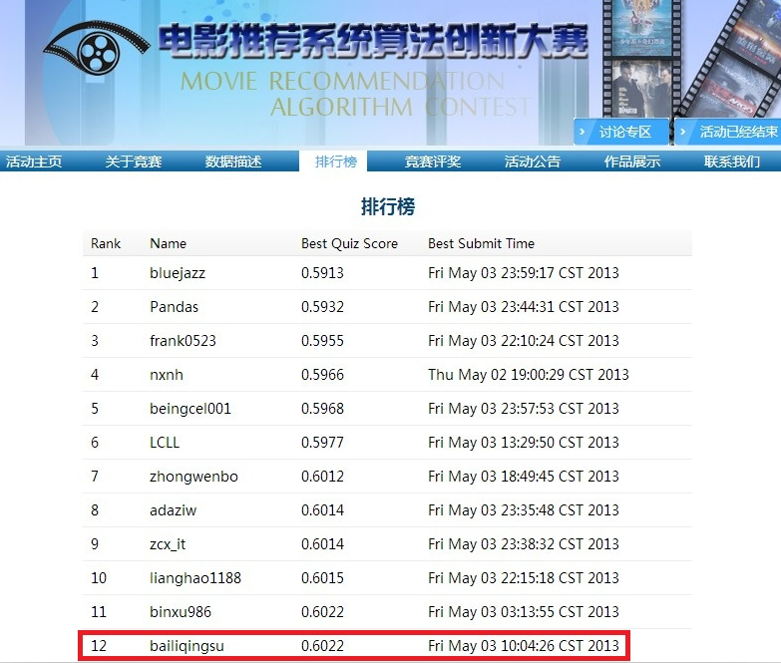
记得刚接触SVD是在大二,那会儿跟师兄在做项目的时候就用到这个东西,然后到大三下学期刚好百度举办了一个电影推荐算法大赛,跃跃欲试地参加了,当时就用的SVD而且只会用这个,后来觉得效果还不错,接着就又找来了Koren的论文,看了一下把SVD++也实现了,把两者结果融合得到不少的提升。下面是最终比赛结果:
其实这个最终结果是和第11名组队后融合了他的结果,所以成绩是一样的。但是单纯地使用SVD、SVD++融合得到的结果最好的也能到0.606左右,这个结果已经很牛逼了,记得当时0.6111在榜上维持了两个多星期的No.1。当时的遗憾就是没能实现更多的SVD扩展算法,导致融合的结果没法再提升,代码也由于时间仓促写的很臃肿,前段时间有空把算法重写了一下并实现了更多的扩展算法,已经共享到github上了,有兴趣的可以看看:https://github.com/jingchenUSTC/SVDRecommenderSystem
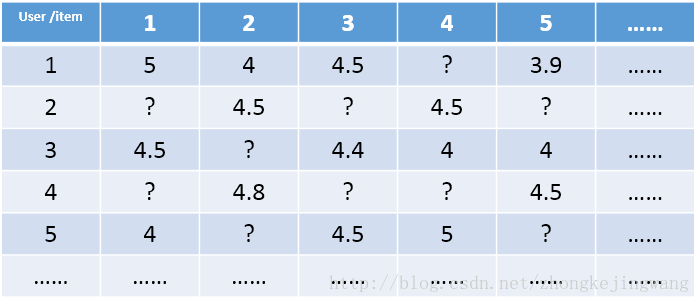
下面开始介绍SVD算法,假设存在以下user和item的数据矩阵:
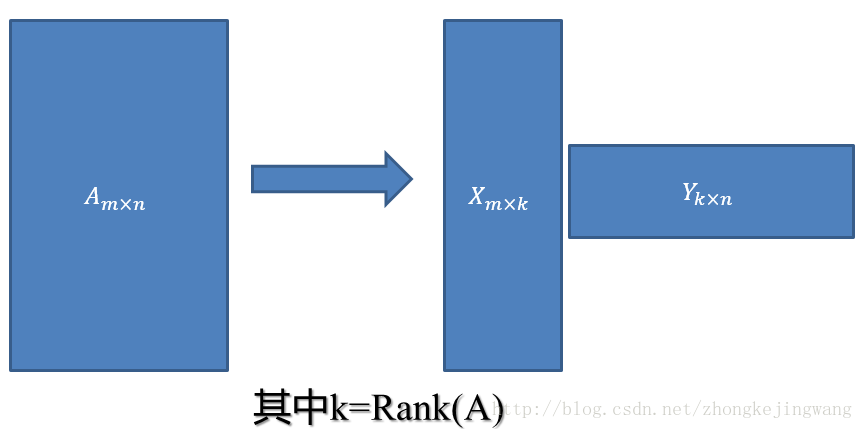
这是一个极其稀疏的矩阵,这里把这个评分矩阵记为R,其中的元素表示user对item的打分,“?”表示未知的,也就是要你去预测的,现在问题来了:如何去预测未知的评分值呢?上一篇文章用SVD证明了对任意一个矩阵A,都有它的满秩分解:
那么刚才的评分矩阵R也存在这样一个分解,所以可以用两个矩阵P和Q的乘积来表示评分矩阵R:
上图中的U表示用户数,I表示商品数。然后就是利用R中的已知评分训练P和Q使得P和Q相乘的结果最好地拟合已知的评分,那么未知的评分也就可以用P的某一行乘上Q的某一列得到








 本文详细介绍了Singular Value Decomposition (SVD) 在推荐系统中的应用,包括基本SVD、Regularized SVD (RSVD)、Asymmetric SVD (ASVD) 和 SVD++ 算法的推导与解释。通过梯度下降法优化目标函数,以最小化预测评分与实际评分的误差。此外,讨论了正则化如何防止过拟合,以及对偶算法在某些情况下的优势。作者分享了实现这些算法的代码仓库链接。
本文详细介绍了Singular Value Decomposition (SVD) 在推荐系统中的应用,包括基本SVD、Regularized SVD (RSVD)、Asymmetric SVD (ASVD) 和 SVD++ 算法的推导与解释。通过梯度下降法优化目标函数,以最小化预测评分与实际评分的误差。此外,讨论了正则化如何防止过拟合,以及对偶算法在某些情况下的优势。作者分享了实现这些算法的代码仓库链接。
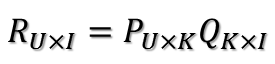
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








