本章的注意力集中在数据点不是独立同分布的情况。具体来说,集中在沿着时间序列进行的测量数据。
顺序分布分为静止的和非静止的两种。在静⽌分布中,数据会随着时间发⽣变化,但是⽣成数据的概率分布保持不变。对于更复杂的⾮静⽌分布的情形,⽣成概率本⾝会随着时间变化。这⾥关注的是静⽌分布。
这一章主要讲解隐马尔科夫模型和线性动态系统。它们都是马尔科夫模型衍生出来的,区别是如果潜在变量是离散的,模型变成了隐马尔科夫模型,潜在变量是连续且服从高斯分布的,模型变成线性动态系统。这两个模型的推导和求解非常相似,这里主要介绍隐马尔科夫模型,线性动态系统的推导和预测也与它相似,但由于是高斯模型,推导过程其实会变得比较复杂,本人也没太看懂,所以此处不作介绍
马尔科夫模型
对于一个观测序列,我们用概率的乘积规则来表⽰它的联合概率分布
假设右侧的每个条件概率分布只与最近的⼀次观测有关,⽽独⽴于其他所有之前的观测,那么就得到了⼀阶马尔科夫链。
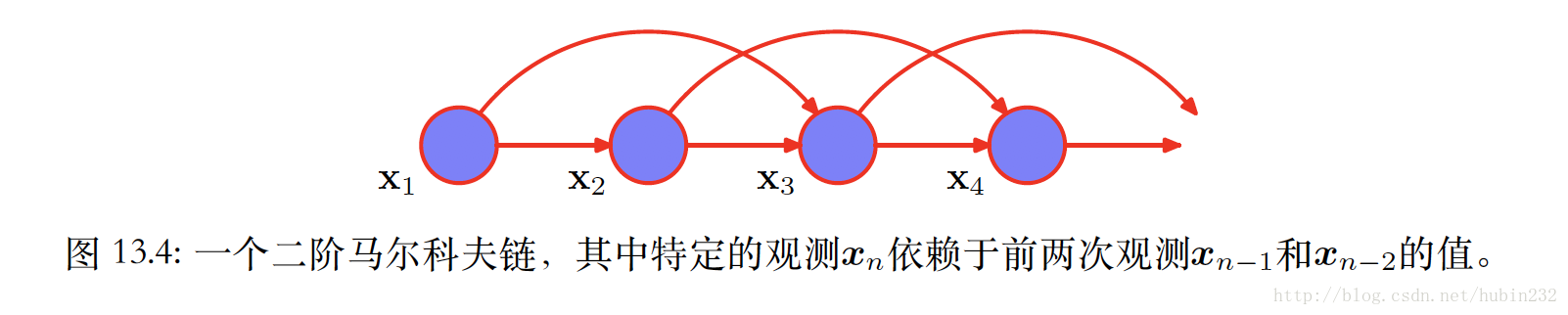
虽然这⽐独⽴的模型要⼀般⼀些,但是仍然⾮常受限。对于许多顺序的观测来说,预计若⼲个连续观测的数据的趋势会为下⼀次预测提供重要的信息。⼀种让更早的观测产⽣影响的⽅法是使⽤⾼阶的马尔科夫链。如二阶马尔科夫链。
然而,这种阶数的增长是有代价的,模型的参数会随阶数的增长而指数增长。
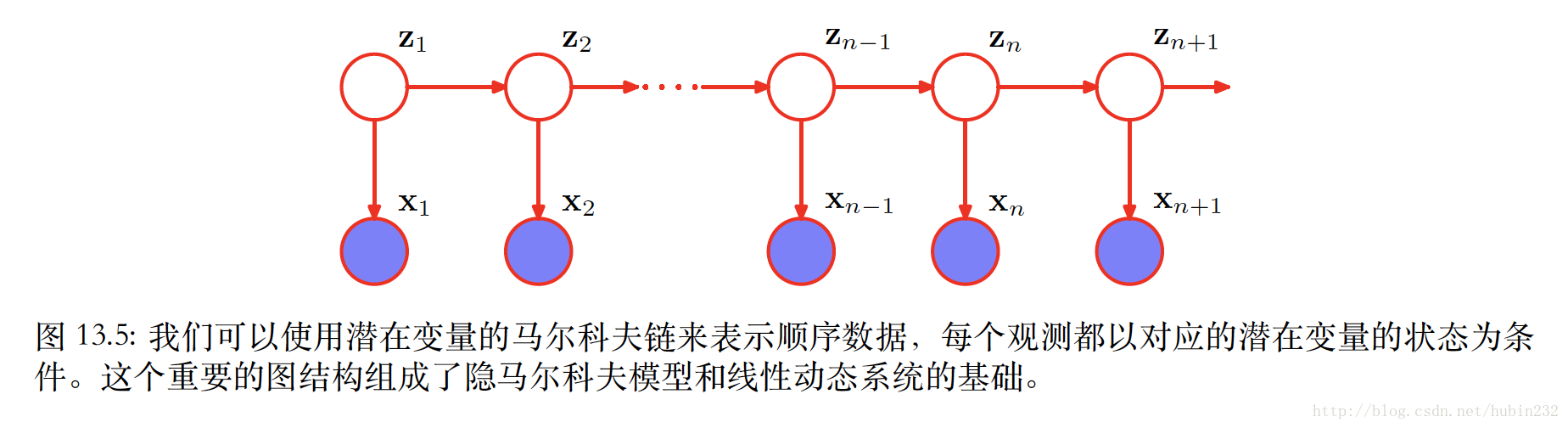
我们希望构造任意阶数的不受马尔科夫假设限制的序列模型,同时能够使⽤较少数量的⾃由参数确定。引⼊额外的潜在变量使得更丰富的⼀类模型能够从简单的成分中构建。现在我们引入如下图依赖关系的隐变量 zn
则模型对应得到联合概率分布为:
用d-划分准则的观点分析,总存在⼀个路径通过潜在变量连接了任意两个观测变量 xn 和 xm ,并且这个路径永远不会被阻隔。因此对于观测变量 xn+1 来说,给定所有之前的观测,条件概率分布 p(xn+1|x1,...,xn) 不会表现出任何的条件独⽴性。
隐马尔科夫模型
模型介绍
基本假设:
(1) 齐次马尔科夫假设:假设隐藏的马尔科夫链在任意时刻t的状态只依赖其前一时刻的状态,与其他时刻的状态和观测无关,也与时刻t无关
(2) 观测独立性假设:假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测和状态无关
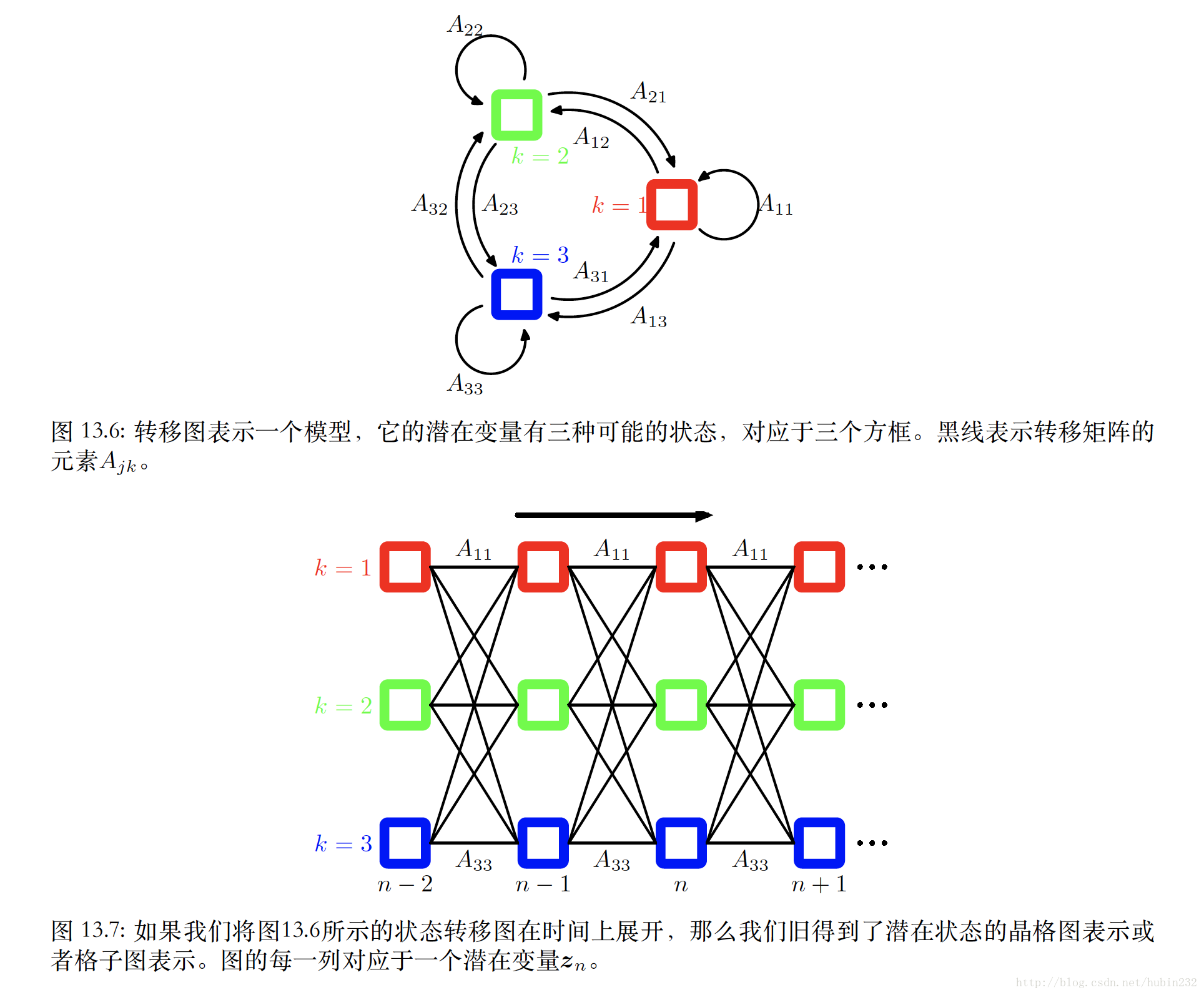
这个模型中,潜在变量 zn 是离散的。它有三个重要的概率,即转移概率(转移概率矩阵用A表示),初始概率(初始概率矩阵用 π 表示)和生成观测变量的概率(用 ϕ 表示)
我们假设 zn 服从多项式分布,并让它通过条件概率分布 p(zn|zn−1) 对前一个潜在变量 zn−1 产生依赖。假设由于潜在变量是K维⼆值变。则转移矩阵A满足 Ajk≡p(znk=1|zn−1,j=1) ,且 0≤Ajk≤1 , ∑kAjk=1 。则转移概率可以写成:
初始结点的概率用 π ,其元素为 π≡p(zk=1) ,即
对于生成观测变量的概率,可以表示如下,其中, ϕ 是控制概率分布的参数集合。
因此,观测变量和潜在变量的联合概率分布为:
其中, X={x1,...,xN} 是观测变量, Z={z1,...,zN} 是隐变量,而 θ={π,A,ϕ} 是控制模型参数的集合。
最大似然求解(学习问题)
学习问题是指给定观测序列,想预测模型的参数 θ={π,A,ϕ} ,看看哪些参数是最有可能的模型
如果我们观测到⼀个数据集 X={x1,...,xN} ,那么我们可以使⽤最⼤似然法确定HMM的参数。似然函数通过对联合概率分布中的潜在变量进⾏求和的⽅式得到,即
下面通用EM算法求解。开始阶段是对模型参数的某些初始的选择,我们记作 θold 。在E步骤中,我们使⽤这些参数找到潜在变量的后验概率分布 p(Z|X,θold) 。然后,我们使⽤这个后验概率分布计算完整数据似然函数的对数的期望,得到了⼀个关于参数 θ 的函数 Q(θ,θold) ,定义为:
为了方便表示,定义:
进一步定义,如下:
现在,我们将所有的公式整理,得到Q的结果:
现在,E步骤的目标是高效的计算 r(zn) 和 ξ(zn−1,zn) ,后面前向后向算法中说明。M步骤是关于参数 θ={π,A,ϕ} 最大化 Q(θ,θold) ,其中,将 r(zn) 和 ξ(zn−1,zn) 看做常数。
用拉格朗日乘子法求得(这个各个参数都是转移函数,即是概率的形式,存在约束):
对于 ϕk ,只有最后一项依赖于它,这⼀项的形式与独⽴同分布数据的标准混合分布的对应的函数中的数据依赖项完全相同。我们可以简单地最⼤化发射概率密度 p(x|ϕk) 的加权的对数似然函数,权值为 r(znk) 。假设发射密度函数是高斯的,即 p(x|ϕk)=N(x|uk,Σk) ,则最大化Q得:
不同的先验分布,观测概率分布 p(x|ϕk) 会是不同的结果。
前向后向算法
这个算法主要是高效计算刚刚E步骤所需得 r(zn) 和 ξ(zn−1,zn) 。
首先考虑 r(zn)
这里,定义了
而 ξ(zn−1,zn) 又可以表示为:
这里
p(xn|zn)
是发射概率
ϕ
,
p(zn|zn−1)
是转移概率
A
,因此,只需知道
下面,只需要探索高效求取 α(zn) 和 β(zn) 即可。
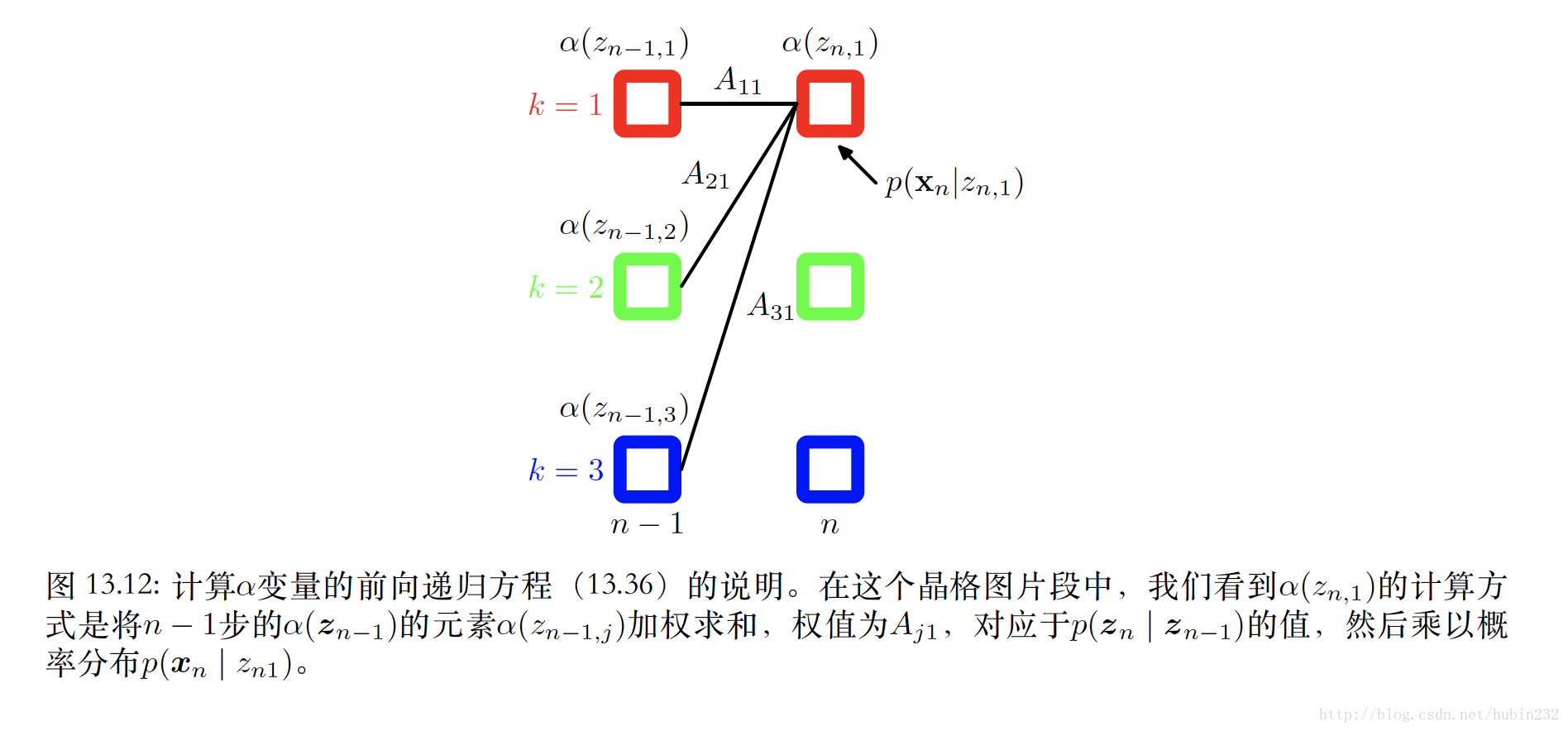
前向传播:
则得到对应的前向递推公式:
其中
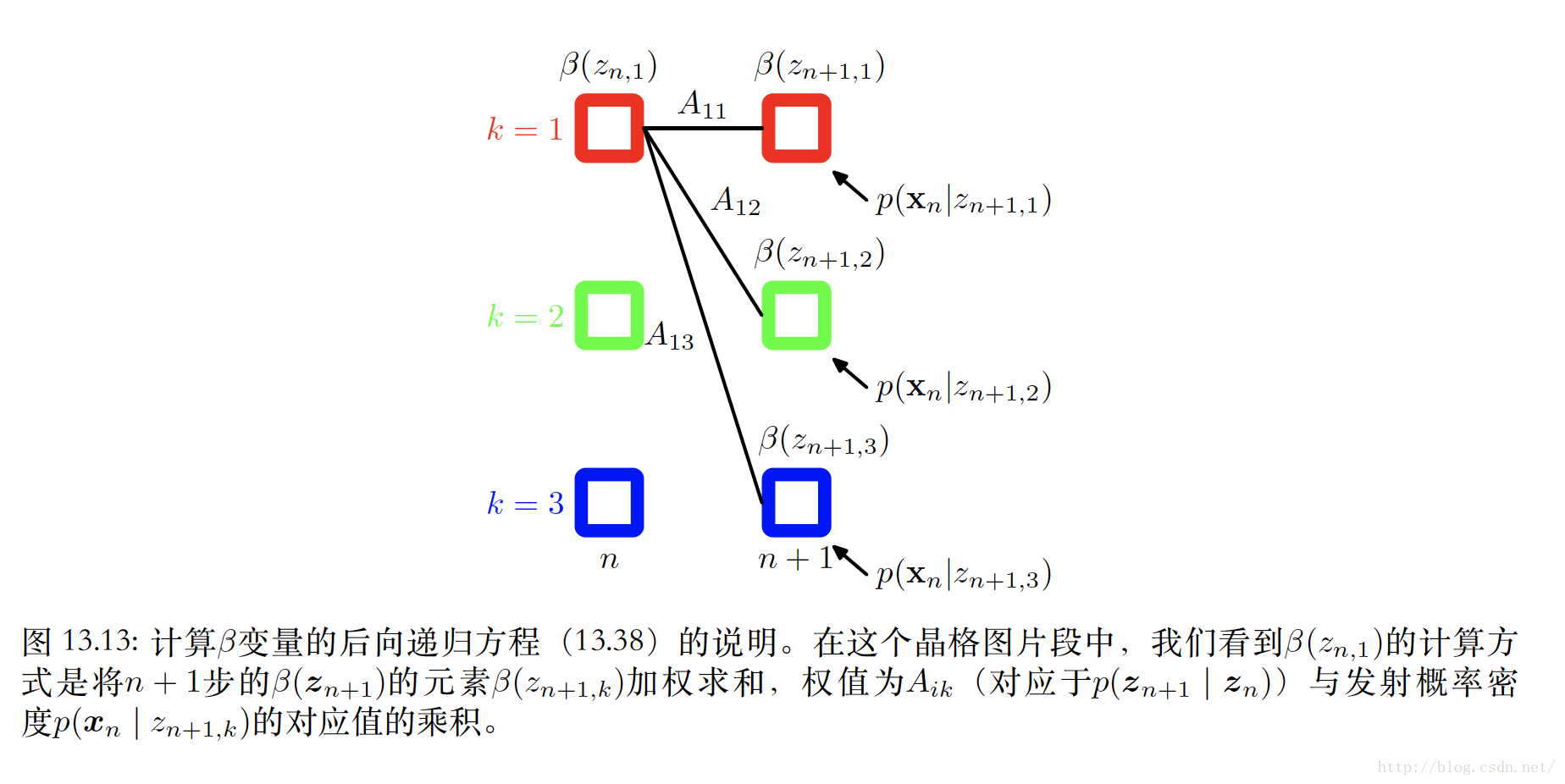
后向传播:
则得到对应的后向递推公式:
其中
这里得到的结果其实也可以用图模型的角度去分析,通过构造因子图得到前向后向传播的递推关系,结果将和上面一致。这里省略
缩放因子
上面的递推其实还存在问题,因为 α(zn) 和 β(zn) 的递推式是概率连乘的形式,在递推过程中会不断减小,指数地趋于零。因此需要一个归一化版本的结果。
归一化版本:
我们定义:
则:
因此:
前向递推公式为:
同理
后向递推公式为:
对应的 r(zn) 和 ξ(zn−1,zn) 为:
预测问题
分析预测问题,有:
维特比算法(对应解码问题)
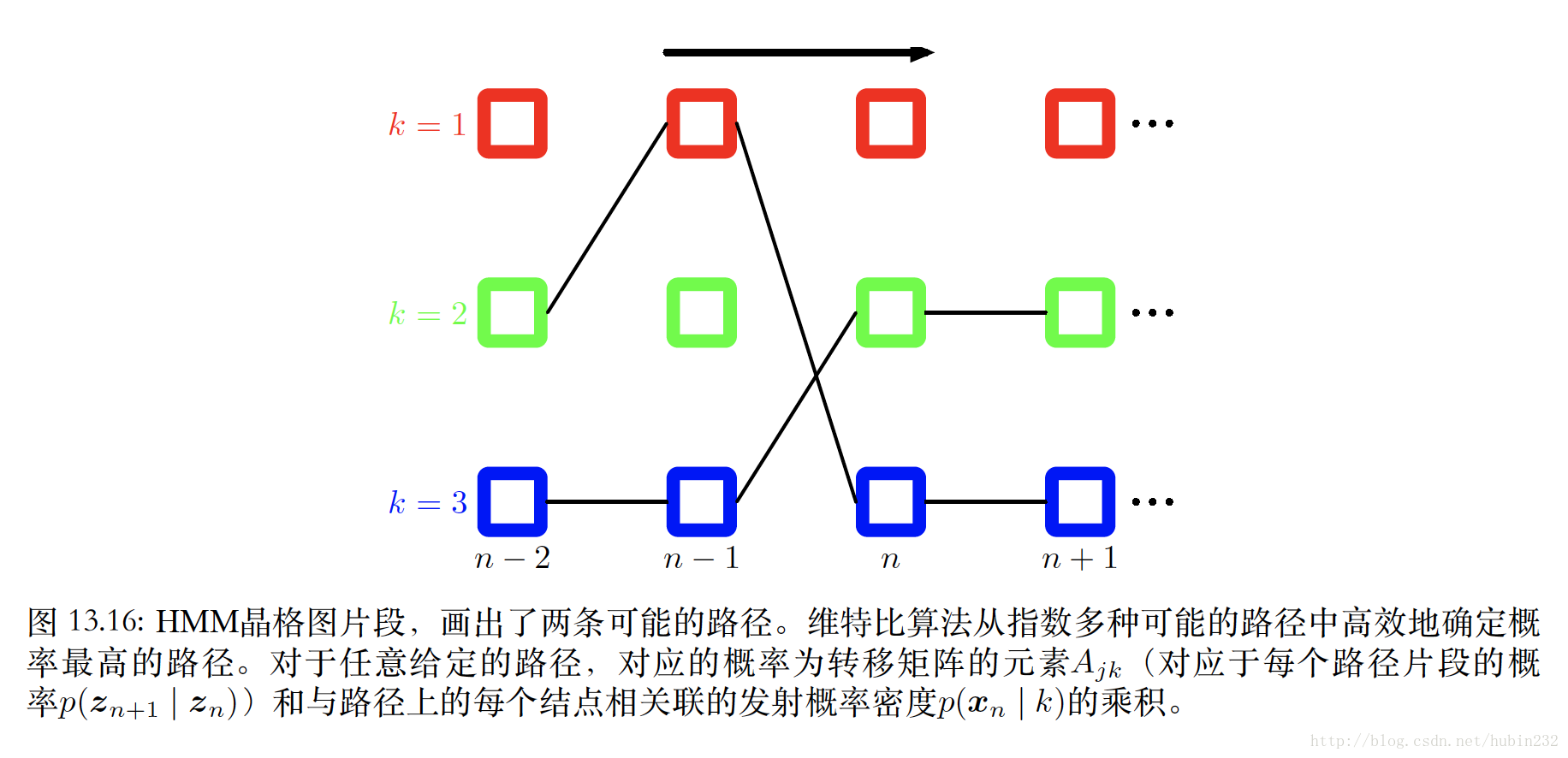
所谓解码问题,是指给定的观测序列,寻找概率最⾼的隐含状态序列。这个问题可以使⽤最⼤加和算法⾼效地求出,这个算法在隐马尔科夫模型中被称为维特⽐算法。
这部分看得不是很懂,个人理解来看,维特比算法其实就是动态规划,如果我们知道第n-1个时刻,在K个状态下,分别对应观测的最大概率的状态序列 {z1,k,...zn−1,k} ,那么下一时刻,对应观测的最大概率的状态序列,必然是由这K个状态下的,对应观测的最大概率的状态序列衍生出来的,所以,第n-1个时刻,我们只需要保留K个状态下对应的最大概率序列(K个序列)。第n时刻也一样,这就将运算复杂度从 O(KN) 转为 O(NK) 。






















 1161
1161











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








