一些基本的理论
了解一些PCA的都知道,里面使用了协方差矩阵的特征分解.先介绍一些协方差与统计相关性,接着再引入具体的PCA方法.
方差:
在概率论和统计学中,一个随机变量的方差描述的是它的离散程度,也就是该变量离其期望值的距离。一个实随机变量的方差也称为它的二阶矩或二阶中心动差,恰巧也是它的二阶累积量。
某个变量的反差越大,不确定度越大,就信息论而言,其包含的信息越大.
协方差:
协方差(Covariance)在概率论统计学中用于衡量两个变量的总体误差。
期望值分别为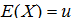
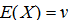
一个线性相关性度量指标:皮尔森相关系数,与协方差有很大关系(为其分子).
而皮尔森相关系数,又是自身标准化后的余弦距离
(具体可见另一篇blog: http://blog.csdn.net/ice110956/article/details/14143991).
回忆一下余弦定理:
也就是两个向量的夹角,夹角越大,方向相差越大,线性相关性越小.平行向量的夹角为0或180.
简单得做如下归纳,有不对的地方望指正:
协方差->皮尔森相关系数->余弦夹角.
简单用余弦夹角来解释协方差,就是说,协方差表征了两个向量的线性相关性.
如果两个变量线性相关,他们的夹角为0,余弦系数与协方差系数都为1,一个变量可以由另一个变量完全表示.用信息论的说法,就是其中一个的信息量为0,即冗余信息.
如果他们线性相关性很低,也就是夹角很大,协方差为0,两者没有相似信息,也就很少冗余信息.
具体到实践中,我们希望样本的每一维都是有用信息,都与其他维线性无关,也就少了冗余信息,也就是两两的协方差为0;那么就要用到下面的协方差矩阵.
协方差矩阵
在统计学概率论中,协方差矩阵是一个矩阵,其每个元素是各个向量元素之间的协方差。
假设X是以n个随机变量组成的列向量
并且ui是其第i个元素的期望值,即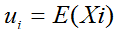
上面需要注意的是
协方差矩阵中的每一个元素是表示的随机向量X的不同分量之间的协方差,而不是不同样本之间的协方差,如元素(I,j)就是反映的随机变量Xi,Xj的协方差。
(这点在刚学习PCA的时候容易弄混了,以为是样本之间的协方差,其实是每一维之间的协方差)
协方差矩阵的对角元素是变量X自身的方差.
根据我们上面关于协方差,方差的知识,我们可以得出如下结论:
如果两个元素Xi,Xj的协方差项(I,j)=0,那么这两个变量线性无关.
如果对角元素(ii)为所有对角元素最大,那么对应的变量Xi所蕴含的信息最大.
那么,如果n个变量矩阵的协方差矩阵为对角矩阵,那么其所有变量两两间线性无关(没有冗余信息);并且,对角元素最大项的信息量最大.
OK,利用上面的知识,我们开始讨论PCA.
PCA理论说明
PCA的n个随机变量构成的的矩阵如下:
(注意,这里的n表示维数,不是样本数);
直观的目标:
我们想要寻找一个线性变换,使得变换后变量两两线性无关,能量集中到较少的几个变量中,并且按照大小重新排列.,变换后,我们可以相应地舍去后面几个能量小的分量,达到降维的目的.
(关于PCA的其他直观的目标,我们再后面讨论)
上面的目标,我们用协方差矩阵来表征,就是寻找一个线性变换,使得其协方差矩阵为对角阵.
现在问题变为,如何寻找一个线性变换,使得投影后的协方差矩阵为对角阵.
关于线性变换与特征向量的进一步知识,可参考另一篇相关日志(http://blog.csdn.net/ice110956/article/details/14228013)
回忆矩阵的对角化方法,
求出其所有特征向量,组成线性变换矩阵即可.
对角化协方差矩阵,用到协方差矩阵E的特征向量矩阵,记为P.我们再用这个P变换X,得到Y
则有
在简单归纳上面推导:变换P使得协方差矩阵变为对角,也使得原矩阵X变换为Y后,Y的新协方差矩阵是对角阵
进一步的,我们通过构造P的特征向量的顺序,使得特征值大的排在前面.通过这种方法变换后,能量大的变量总在最前面.
当我们降维时,直接去掉排在后面的特征向量,生成低维的P即可.
小结:上面用协方差矩阵与相关性的角度,整理了PCA的基本原理.
PCA的直观理解
1. 斯坦福公开课上的理解:
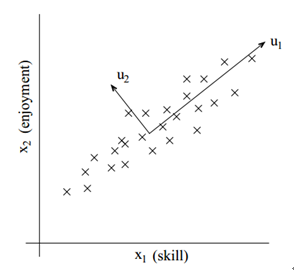
上图我们可以看出,二维样本在u1方向上的方差最大(也就是能量最大,信息量最大),u2方向上的能量最少;
通过线性变换,我们可以用正交的u1,u2来重建坐标系,从而使方差集中在第一个分量上(u1方向)
如果要从二维降到一维,很明显的,投影到u1方向能够保留最多的信息,我们可舍去u2上的分量.
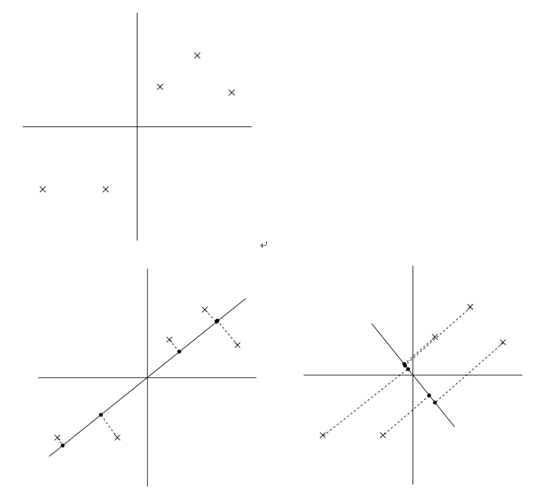
如下图,下面五个点要从二维投影到一维,选择两个不同的方向,得到不同的方差.依据我们上面阐述的方差与信息量的关系,第一个投影后更分散,也就是方差更大,也就是PCA的投影.
于是,这里的PCA直观理解归纳为:最大散度方向(方差)投影
2. 某篇文献上的理解:
三台摄像机记录弹簧小球的运动.三台相机为三个维度,并且这三个维度不是正交的.
我们以这三台相机的方向建立X1,X2,X3三个坐标轴,然后得到三维的数据.
依照物理学的知识我们知道,这个小球的运动用一个维度X就能记录.但是现在我们用了三个维度的相机.有许多噪声以及重复的,无用的信息在里面.
再次根据物理知识,小球在其原来的方向上,方差应该是最大的(信息量最大).极端的,假设一个相机沿着X轴,那么小球是静止的.
我们首先通过坐标变换,得到相互正交的三个方法(其中有一个是X),再选择方差最大的那个,降到一维,就得到了X轴,也就是PCA的效果.
这里的PCA概括为:信息的主方向投影去噪.
PCA的局限性
如下面这幅图:
如果我们想对这两块数据分类,那么1方向应该是最好的方向;但是PCA会选择2方向.
也就是PCA不具有鉴别特性.
针对PCA的非鉴别特性,相应地有LDA等,这里不再赘述.





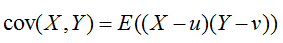


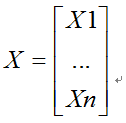

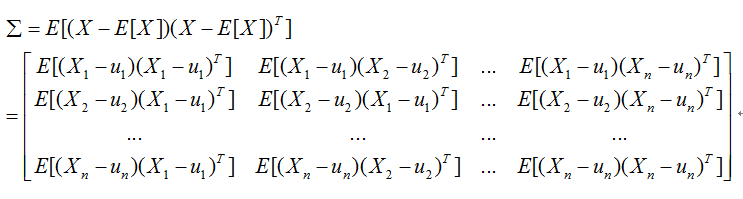



















 507
507

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








