线性映射
首先是wiki上的定义: 在数学中,线性映射(也叫做线性变换或线性算子)是在两个向量空间之间的函数,它保持向量加法和标量乘法的运算。术语“线性变换”特别常用,尤其是对从向量空间到自身的线性映射(自同态)。
线性的定义如下:
设 V 和 W 是在相同域 K 上的向量空间。函数 f : V → W 被称为是线性映射,如果对于 V 中任何两个向量 x 和 y 与 K 中任何标量 a,满足下列两个条件:
可加性:
齐次性 :
这等价于要求对于任何向量 x1, ..., xm 和标量 a1,..., am,方程
成立。
矩阵
如果 V 和 W 是有限维的,并且在这些空间中有选择好的基,则从 V 到 W 的所有线性映射可以被表示为矩阵;
如果 A 是实数的 m × n 矩阵,则规定 f(x) = Ax 描述一个线性映射 Rn → Rm
简单来说就是,线性映射可以用一个矩阵表示.
自同态映射与方阵
在线性映射中,可以把N维向量投影到M维向量,N可以不等于M.
当N==M时,也就是定义中的自同态映射.
特征向量与特征值在自同态的情况下产生.即N维到N维的映射.
看下面几个二维空间自同态映射的例子.
逆时针旋转90 度:
逆时针旋转θ 度:
针对x轴反射:
在所有方向上放大2 倍:
垂直错切:
挤压:
向y轴投影:
这些2*2的方阵,是二维自同态映射矩阵一些特殊例子.
特征向量与特征值的物理意义
先看上面这幅图,把画像水平镜像翻转.画上面有红,橙,黄三个向量.通过翻转,红向量方向没有变,黄为负方向,黄色完全改变了方向.
通过上面线性代数的知识,我们知道,上面的变换是自同态变换,可以用一个方阵矩阵来表示上述变换.
假设翻转变换为A.
上面三个向量的变换,用矩阵点乘表示,如下:
A*red=red;
A*yellow=-yellow;
观察上面的式子,我们发现,与特征向量的定义很相似.
特征向量的定义如下:
下面引入特征向量的物理意义:
在数学上,特别是线性代数中,对于一个给定的线性变换,它的特征向量V经过这个线性变换后,得到的新向量仍然与原来的V保持在同一条直线上,但其长度也许会改变.一个特征向量的长度在该线性变换下缩放的比例称为其特征值.
对于特征向量,线性变换仅仅改变它们的长度,而不改变它们的方向(除了反转以外),而对于其它向量,长度和方向都可能被矩阵所改变。如果特征值的模大于1,特征向量的长度将被拉伸,而如果特征值的模小于1,特征向量的长度就将被压缩。如果特征值小于0,特征向量将会被翻转。
简单概括,就是:线性变换的特征向量表征了这个线性变换的方向.
接下来,引出一个谱定律,把上面的东西可以串起来了.
Spectral theorem的核心内容如下:一个线性变换(用矩阵乘法表示)可表示为它的所有的特征向量的一个线性组合,其中的线性系数就是每一个向量对应的特征值.
写成公式就是:
简单概括,也就是:线性变换是其特征向量的线性组合,特征值指代了其权值.
这下理解线性变换的特征值与特征向量就容易了:线性变换可用矩阵表示,矩阵的特征向量表征方向,特征值表征这个方向的权重.








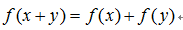
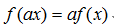
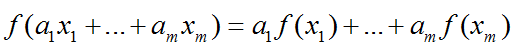
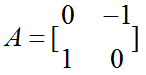

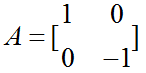
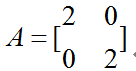
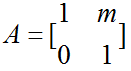
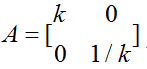
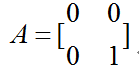

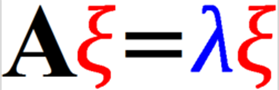
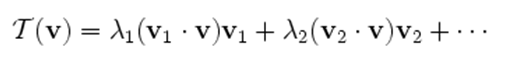














 5515
5515

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








