最大流/最小割(Max-Flow/Min-Cut)算法,因其可以对能量方程最小化进行求解,在计算机视觉(CV)中有很广泛的应用。之前介绍过的Seam Carving算法(用于图像智能缩放),或是图像分割算法中,经常使用最大流/最小割进行能量方程的最小化求解。
1. 最大流/最小割 背景介绍
最大流/最小割(Max-Flow/Min-Cut)在解决计算机视觉中的能量方程最小化问题的强大,最早发现是Greig于1989年发表的文章:Exact Maximum A Posteriori Estimation for Binary Images。
最大流最小割算法求解的能量方程,通常是基于图结构得到的能量求解方法,这类能量方程可以普遍表示为:
其中L是图像P的一个标签结果。设P为3*3的图像,P = [ 3, 8, 9; 4, 9, 8; 2, 9, 7 ],现在要将P的像素分为两类,标签值为1或2,L是P的所有可能性中的一种可以是L = [ 1, 2, 2; 1, 2, 2; 1, 2, 2 ] 或 L = [ 1, 1, 2; 1, 2, 2; 2, 2, 2 ](还有很多就不枚举了),L的所有可能性即为2^9,而能量方程 E(L) 就是计算在当前标签结果下的能量值,通常我们将能量方程最小化,从而求出可以使得总体能量最小的标签值情况L,利用最终的像素分类结果得到图像分割等结果。如下图所示,(a)为图像P的像素灰度值示意图,颜色越深则灰度值越小;(b)为该图像的一种分类结果L,当然还存在着若干种分类结果L,我们要做的就是设计一个相较周全的能量方程,然后通过最大流/最小割方法进行最小化求解。
现在返回公式(1)继续解释。式中两项,分别为数据惩罚项Dp(Data Penalties)和互动项Vp,q(Interaction Potentials)。数据惩罚项在某些方法中也成为Unary Potentials,Interaction Potentials通常对应为Pairwise Potentials,顾名思义,数据惩罚项是像素点自身数据值(如:色彩、强度等)的能量评测项,互动项则考虑两两像素间的不连续关系(如空间或时间连续性)对整体能量值的影响,下式Vp,q的搜索范围N是当前像素p的邻域范围,q是其邻点才需要考虑两像素间的能量关系。
2. 能量方程的图结构 介绍
有向图G = < V, E >由节点V和节点间的边E构成。通常来说,图中的节点对应图像的像素或超像素、超体素。图通常还包含一些额外附加但非常重要的点,称为终点(terminals,不要吐槽翻译= =因为本宝宝也不知道应该怎么翻译,理解就行,它们就是一些很重要的终端节点)。终点的重要性在于,它们可以直接连接图中节点,从而给每个节点赋予标签,意味着每个终点表示一个标签值,例如图中有两个终点,则该图像最终只会被分为两种标签值。
以下用包含两个终点的图结构进行更详细的解释,两个终点(terminals)在图结构G中通常成为源点(Source,缩写为s)和汇点(Sink,缩写为t)。
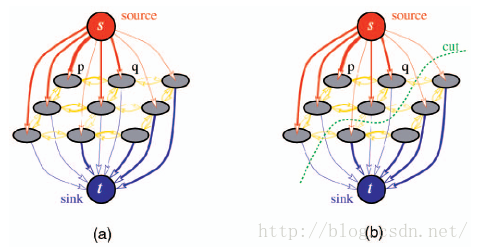
如上图所示,P为3*3的图像,现在要将它的像素划分为s和t两个标签值的子集。图(a)为各节点与源点汇点、节点间的连接关系示意图;图(b)中的cut是图割的示意,通过能量方程的最小化求解,得到图像P的最小割,将不必要节点间的边割断,源点和汇点所连接点的集合的交为空,并为P中所有节点。
值得注意的是,在有向图G中,p点到q点的权值和q点到p点的权值可能会不一样。图中的边分为两类:n-links和t-links。n-links的n是neighbour的缩写,表示节点间的连接边,衡量节点不连续性(两节点不连续性即差异越大,惩罚值越大);t-links的t是terminal的缩写,表示节点与终点(terminal)相连,衡量节点赋予所连接终点须耗费的代价值。两类边的权值分别对应公式(1)能量方程中的互动项Vp,q和数据惩罚项Dp。
以上为视觉中设计能量方程的背景条件之一,构建图结构的方法介绍。
3. 最大流/最小割问题
基于第2节中构造的图结构,图割C通过切断图结构的边,将图中的所有节点划分为两个不相交的子集S和T,其中源点s在子集S中,汇点t在子集T中。因此,图割C定义为其所割断(经过)边( p, q )的权值(代价)总和,其中p属于子集S,q属于子集T。最小割问题,就是在图结构上找到具有最小权值(代价)总和的图割C。
最小割问题通常可以通过找到从源点s到汇点t的最大流求解,即最小割问题和最大流问题是等价的。最大流问题的求解办法通常是使用增广路径算法,Yuri Boykov于2004年提出一个优化求解方法,下面对其进行进一步介绍。
传统的增广路径算法是在图中搜索从源点s到汇点t的路径,使用宽度优先搜索(广搜)将所有路径遍历,最终找到最大流路径。但是这个算法的效率在实际应用中是软肋,因为广搜通常要遍历图中几乎所有的节点,为解决这个问题从而有了优化的新方法。新的方法同样也是增广路径算法的延伸,通过构建树从而找到增广路径,然而不同的是,该方法构建了两棵树,一个从源点s出发,一个从汇点t出发。另一个区别在于新的方法不会从头构建这两颗树,而是复用已有树结构,从而达到提高算法速度的目的。
4. 最大流求解方法
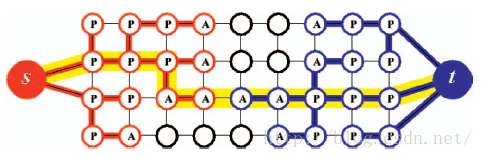
假设以源点s和汇点t在图结构上构造两颗没有交集的树,分别为树S和树T,如下图所示。树S中的所有边都是由父节点指向子节点(存在流量),树T中则由子节点指向父节点。不在两树中的节点为“自由”状态。搜索树S和T中的节点只有两种状态:“主动”和“被动”。主动态的节点表示搜索树的外边界节点,意思是从该节点出发还可以扩展搜索树,而被动态节点表示搜索树内部的节点,树不能由该节点向外扩展。主动态节点因为可以向外扩展,所以有可能会搜索到另一搜索树的节点,当主动节点检测到另一搜索树的节点,就找到了一条增广路径。
Yuri提出的算法主要循环以下三个步骤:
1. “增长”阶段:搜索树S和T扩展节点,直到两树相遇,得到一条由源点s到汇点t的增广路径。
2. “增广”阶段:根据找到的增广路径将搜索树拆分为子树或森林。
3. “领养”阶段:搜索树S和T重新构建。
优化的增广路径求解算法伪代码如下,初始化时,搜索树S只有源点s为主动节点,搜索树T只有汇点t作为主动节点,增长搜索树直到它们的主动节点相遇,得到一条增广路径P。如果P为空则算法终止,反之则对P进行增广流量处理。然后对孤点进行领养处理,以此循环。
4.1 增长阶段
增长阶段中,搜索树扩展。主动态节点搜索相邻且邻边仍有可用流量的自由节点作为搜索树新的子节点,新增长的子节点又称为该搜索树的主动态节点,搜索树继续扩展增长。当主动态节点的所有邻点都检测过,主动态节点变为被动态节点。当两颗搜索树的主动态节点搜索到对方的节点时,增长阶段终止。然后根据当前建树情况,找到一条增广路径,如上图中黄色路径所示。
增长阶段的伪代码如下所示,该阶段总括一句话就是从自由节点中扩展当前搜索树的新子节点。
其中A是当前搜索树的主动态节点集合,tree_cap( p->q ) 指的是当前节点p到邻点q的边流量值,TREE( q )即节点q所属搜索树标签值,PARENT( q )为节点q的父节点。
4.2 增广阶段
这个阶段根据增长阶段找到的增广路径进行增广流量统计,即求出经过该路径的最大流量,意味着路径中至少有一条边达到饱和态,也就是所经流量等于该边的流量值。因此搜索树S和T中会出现一种新的节点,称为“孤点”(orphans),意思就是连接它与其父节点的边已达饱和态,没有流可以再到达这个节点,好似孤星一般没有人找到(原谅我的修辞)。所以在增广阶段搜索树S和T可能会拆分为多棵子树,从而形成森林。源点s和汇点t仍充当两颗子树的根节点,而孤点成为其余子树的根节点。
增广阶段的伪代码如下,输入是一条由源点s到汇点t的增广路径P,初始时孤点集合为空。
首先找到路径P的瓶颈值,即最小流量边,为该路径的最大流量值。流量经过后,路径P中至少有一条边变为饱和态,即所经流量等于自身流量值,该边连接的子节点变为孤点。
4.3 领养阶段
领养阶段字面上理解就能看出是针对孤点进行处理的阶段,该阶段也是为了恢复搜索树S和T的单一性,即图中除了两颗搜索树,其余节点都归为主动态、被动态和自由态,消除孤点。做法是为每个孤点找到一个新的合法父节点,该父节点原来必须与孤点属于同一搜索树,而且父节点与孤点间有一条未饱和(仍有可经流量)的边。若没有符合要求的父节点,该孤点变为自由节点。以此处理所有孤点和孤点的子节点。当所有孤点都处理后,领养阶段结束,最终只剩下原有的搜索树S和T。
领养阶段的伪代码如下,O为孤点集合,最终变为空集。该阶段中,我们尽力为O的每个节点p找到一个合法父节点,若没有,该节点则恢复为自由节点,其所有子节点变为孤点。
伪代码中的process p分为以下步骤:
1. 首先,尽力找到p的一个合法父节点q,条件为该节点q必须与孤点p为同一搜索树,即TREE( q ) = TREE( p ),并且两节点间的边流量大于0,边为未饱和状态,即tree_cap( q->p ) > 0,且节点q的最原始根节点必须是源点s或汇点t,其它子树的子节点不行。
2. 如果没有为节点p找到合法父节点,节点p变为自由节点,其子节点变为孤点。
最大流的求解过程就是循环重复以上三个阶段,直到搜索树S和T不能再增长。








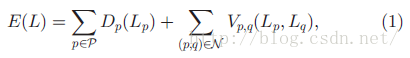


















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








