ACM—动态规划-数塔

HDU 2084

一、题目

在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

输入

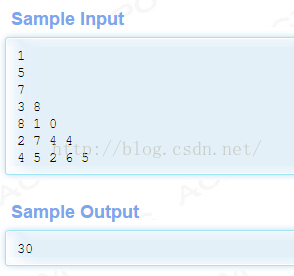
输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。

输出

 

 对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。

 

二、思路

该题有两种解题思路：

1.     顺推法

从数塔的顶部向下推，每个数（除去边界）向上有两个分支，比较上面两个分支数（指的是加完后的新的数塔）的大小，哪个数大就将那个数再加到本位置上面，直到最后一层。则最大的数字之和就是最后一行中最大的那个数。

其动态规划方程为：

F[0][0] = A[0][0];

F[i][0] = F[i-1][0]+A[i][0];

F[i][i] = F[i-1][i-1]+A[i][i];

F[i][j] = max{F[i-1][j-1],F[i-1][j]}+A[i][j];

最终答案为max{F[n-1][j],0<=j<=n-1};

2.     逆推法

从数塔的最低一层开始向上推，比较相邻的两个数（加完后的数）的大小，哪个数大就加到上一层中的那个数上面，直到加到最上面一层，则最大的数就是第一层的那个数。

其动态规划方程为：

G[n-1][j] = A[n-1][j]  0<=j<=n-1;

G[i][j] = max{G[i+1][j],G[i+1][j+1]}+A[i][j];

最后答案为G[0][0];

 

三、代码实现

1.顺推法

#include<stdio.h>
#define N 100
int A[N][N];
int F[N][N];
 
int main()
{
    int i,j,n;
    scanf("%d",&n);
    for(i = 0; i < n; i++)
        for(j = 0; j <= i; j++)      //注意j是从0到i，而不是从0到n-1
            scanf("%d",&A[i][j]);  //将数塔存入A[N][N]数组中。
    F[0][0] = A[0][0];          //边界处理
    for(i = 1; i < n; i++)
        for(j = 0; j < n; j++)
        {
            if(j == 0)
                F[i][j] = A[i][j] + F[i - 1][j];   //边界处理
            else if(j == i)
                F[i][j] = A[i][j] + F[i - 1][j - 1];   //边界处理
            else
            {
                if(F[i - 1][j - 1] > F[i - 1][j])      //动态规划方程核心
                    F[i][j] = F[i - 1][j - 1] + A[i][j];
                else
                    F[i][j] = F[i - 1][j] + A[i][j];
            }
        }
    int max = F[n - 1][0];
    for(j = 1; j < n; j++)       //求最大值MAX
        if(max < F[n - 1][j]) max = F[n - 1][j];
    printf("%d\n",max);
    return 0;
}

2.逆推法

#include<stdio.h>
#define N 100
int A[N][N];
int G[N][N];
 
int main()
{
    int i,j,n;
    scanf("%d",&n);
    for(i = 0; i < n; i++)
        for(j = 0; j <= i; j++)    //注意j是从0到i，而不是从0到n-1
            scanf("%d",&A[i][j]);    //将数塔存入A[N][N]数组中。
    for(j = 0; j < n; j++)         //边界处理
        G[n - 1][j] = A[n - 1][j];
    for(i = n - 2; i >= 0; i--)      //注意i的范围
        for(j = 0; j <= i; j++)
        {
            if(G[i + 1][j] > G[i + 1][j + 1])
                G[i][j] = G[i + 1][j] + A[i][j];
            else
                G[i][j] = G[i + 1][j + 1] + A[i][j];
        }
    printf("%d",G[0][0]);      //结果就是G[0][0]
    return 0;
}