上篇博文我重点介绍了八大内部排序,这篇博文(数据结构与算法的最后一课)重点介绍查找,我们依旧沿用上篇博文的风格,先简单介绍,再以例子重点讲解。
下面我们开始今天的旅行,首先祝你旅行愉快,呵呵。
静态查找
若查找目的是为了查询某个特定的数据是否在表中或检索某个特定数据的各种属性,则此类查找表为静态查找表。
1、顺序查找
基本原理:从表一端开始逐个和关键字进行比较,若找到一个记录和给定值相等,则查找成功,反之失败。再简单点就是,一个一个的比大小,看看是否相等。
例子:
顺序查找更适合于顺序存储结构和链式存储结构的查找表。顺序查找需要一个个的去比较,效率很低。
2、折半查找(二分查找)
基本原理:1.把序列分成左中右三部分,左部分小于中间值,右部分大于中间值;
2.把给定值与中间值比较,确定下次查找是在左部分还是右部分;
3.继续上面两步操作,直到成功或失败。
注意:折半查找需要注意给定的序列必须是一个有序序列。
例子:

3、分块查找
基本原理:顺序查找和二分法查找的折中,先分块,在块中顺序查找。
注意:分成的各块内部数据可能无序;各块之间有序(第二个块中的元素都比第一个块中元素都大);建立了索引表,索引表按关键字有序。
例子:
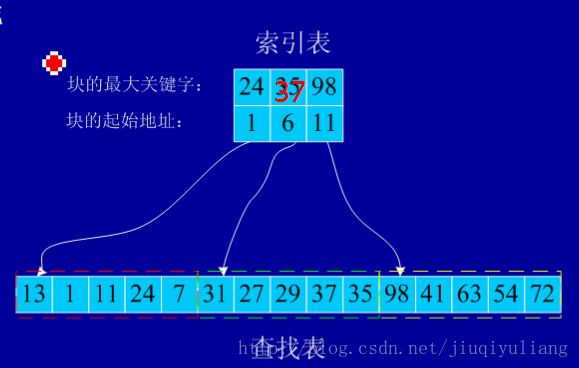
静态查找表方法的性能分析
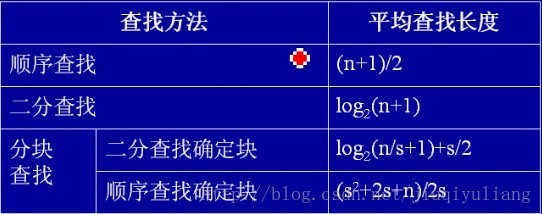
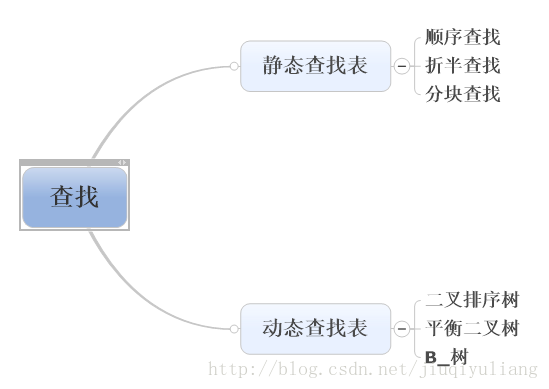
对于动态查找的插入和删除不是特别好讲,我们就不在这里讲了,只是简单的介绍一下什么是二叉排序树和平衡二叉树,B_树只做了解。
动态查找
若再查找的过程中同时插入查找表中不存在的数据,或从查找表中删除已存在的某个数据,则称此类查找表为动态查找表。
1、二叉排序树
定义:1.若它的左子树非空,则左子树上所有的结点的值均小于根结点的值;
2.若它的右子树非空,则右子树上所有的结点的值均大于根结点的值;
3.左右子树本身就是两棵二叉排序树。
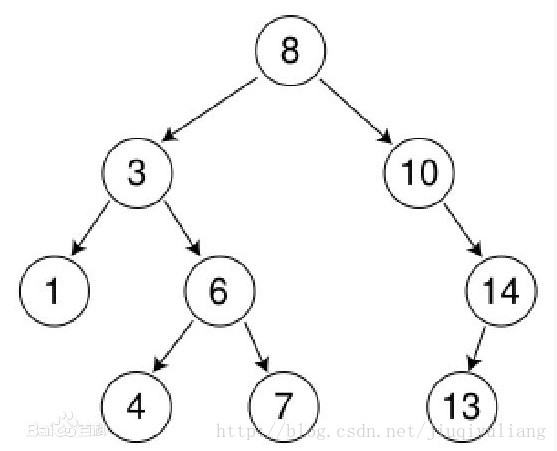
例子:
定义看上去不是特别好理解,其实特别简单,我们再以例子简单的说一下。左子树的所有节点:3,1,6,4,7,都小于父节点8,右子树所有节点:10,14,13,都大于父节点。什么时候都是父节点大于左孩子,小于右孩子例如:8>3,8<10;3>1,3<6。
2、平衡二叉树
定义:1.它或者是一棵空树
2.或者树中任一结点的左右子树深度相差不超过1。
注意:从定义我们可得到:想要一颗树平衡,有三种情况,节点的平衡度要么为了0,要么为1,要么为-1。(平衡度:节点左子树的高度减去其右子树的高度。)
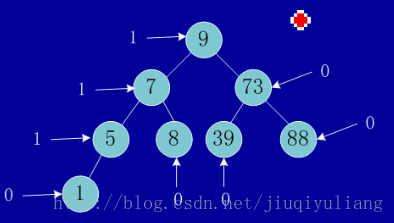
例子:
上面图在每个节点上标出了平衡度,所有的节点的平衡度的绝对值都小于等于0或1,所以它是一棵平衡二叉树。
总结
数据结构和算法的内容到今天(5月16日)就算结束了(祝旅行愉快),由于距离考试很近了,我们后面的博文就开始介绍软考的大题部分的内容,近期就会推出,敬请期待。
后续博客的更新列表,敬请期待。
我的软考之路(一)——开篇(已更新)
我的软考之路(二)——J2SE宏观总结(已更新)
我的软考之路(三)——数据结构与算法(1)之线性表(已更新)
我的软考之路(四)——数据结构与算法(2)之树与二叉树(已更新)
我的软考之路(六)——数据结构与算法(4)之八大排序(已更新)







 本文深入探讨静态查找和动态查找的区别与实现方法,包括顺序查找、折半查找、分块查找、二叉排序树及平衡二叉树等算法。通过实例分析,帮助读者掌握查找表的高效应用。
本文深入探讨静态查找和动态查找的区别与实现方法,包括顺序查找、折半查找、分块查找、二叉排序树及平衡二叉树等算法。通过实例分析,帮助读者掌握查找表的高效应用。


















 294
294












