算法：图的广度优先遍历（Breadth First Search)

图的遍历和树的遍历类似，我们希望从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历（Traverse Graph)。

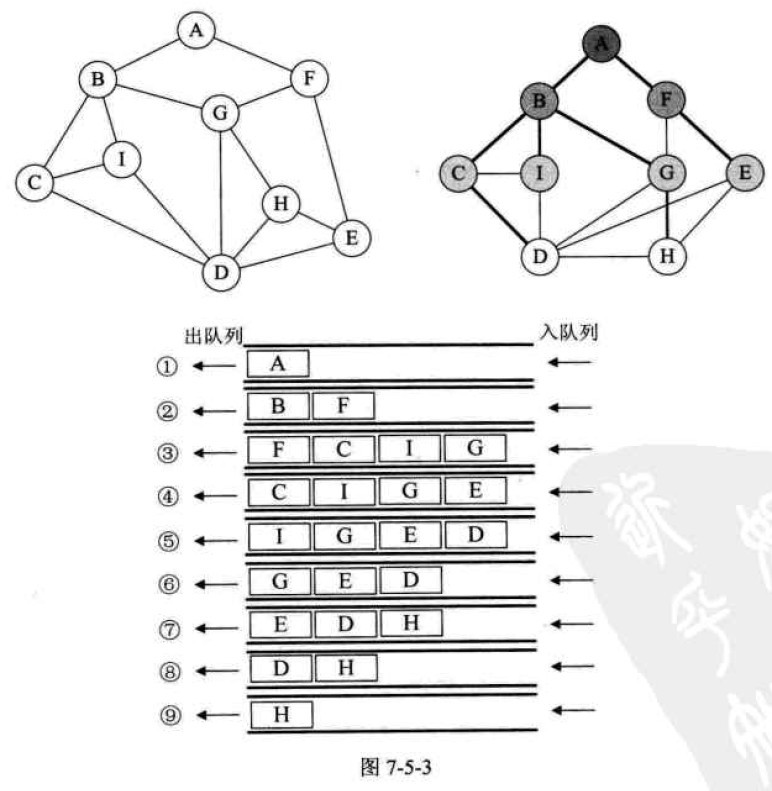
图的遍历方法一般有两种，第一种是我们在前面讲过的《深度优先遍历（Depth First Search)》,也有称为深度优先搜索，简称为DFS。第二种是广度优先遍历（Breadth  First Search)，也有称为广度优先搜索，简称为BFS。我们在《队列与广度优先搜索》中已经较为详细地讲述了广度优先搜索的策略，这里不再赘述。如果说图的深度优先遍历类似树的前序遍历，那么图的广度优先遍历就类似于树的层序遍历了，我们把图7-5-3的第一幅图稍微变形成第二幅图所示，这样层次感就更强了，广度优先遍历需要用到队列的操作，可以参考《队列的顺序存储结构》。

下面只给出邻接矩阵和邻接表存储方式时的图的广度优先遍历的算法代码，没有给出整体可供测试运行的代码，其实只需要再写一个创建图的函数就可以进行整体测试了，可以参考《邻接矩阵创建图》和《邻接表创建图》

一、如果我们使用的是邻接矩阵的方式，则代码如下：（改编自《大话数据结构》）

 C++ Code 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

typedef  char VertexType;  /* 顶点类型应由用户定义 */ typedef  int EdgeType;  /* 边上的权值类型应由用户定义 */ #define MAXSIZE  9  /* 存储空间初始分配量 */ #define MAXEDGE  15 #define MAXVEX  9 typedef  struct {     VertexType vexs[MAXVEX];  /* 顶点表 */     EdgeType arc[MAXVEX][MAXVEX]; /* 邻接矩阵，可看作边表 */      int numVertexes, numEdges;  /* 图中当前的顶点数和边数 */ } MGraph; /* 邻接矩阵的广度遍历算法 */ void BFSTraverse(MGraph G) {      int i, j;     Queue Q;      for (i =  0; i < G.numVertexes; i++)         visited[i] =  false;     InitQueue(&Q); /* 初始化一辅助用的队列 */      for (i =  0; i < G.numVertexes; i++) /* 对每一个顶点做循环 */     {          if (!visited[i]) /* 若是未访问过就处理 */         {             visited[i] =  true; /* 设置当前顶点访问过 */             cout << G.vexs[i] <<  ' ';  /* 打印顶点，也可以其它操作 */             EnQueue(&Q, i); /* 将此顶点入队列 */              while (!QueueEmpty(Q)) /* 若当前队列不为空 */             {                 DeQueue(&Q, &i); /* 将队对元素出队列，赋值给i */                  for (j =  0 ; j < G.numVertexes; j++)                 {                      /* 判断其它顶点若与当前顶点存在边且未访问过  */                      if (G.arc[i][j] ==  1 && !visited[j])                     {                         visited[j] =  true; /* 将找到的此顶点标记为已访问 */                         cout << G.vexs[j] <<  ' ';  /* 打印顶点 */                         EnQueue(&Q, j); /* 将找到的此顶点入队列  */                     }                 }             }         }     } }

遍历结果为：A B F C G I E D H  (上图所示的图结构）

一、如果我们使用的是邻接表的方式，则代码如下：（改编自《大话数据结构》）

 C++ Code 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65

typedef  char VertexType;  /* 顶点类型应由用户定义 */ typedef  int EdgeType;  /* 边上的权值类型应由用户定义 */ #define MAXSIZE  9  /* 存储空间初始分配量 */ #define MAXEDGE  15 #define MAXVEX  9 /* 邻接表结构****************** */ typedef  struct EdgeNode  /* 边表结点 */ {      int adjvex;     /* 邻接点域,存储该顶点对应的下标 */      int weight;      /* 用于存储权值,对于非网图可以不需要 */      struct EdgeNode *next;  /* 链域,指向下一个邻接点 */ } EdgeNode; typedef  struct VertexNode  /* 顶点表结点 */ {      int in;  //结点入度      char data;  /* 顶点域,存储顶点信息 */     EdgeNode *firstedge; /* 边表头指针 */ } VertexNode, AdjList[MAXVEX]; typedef  struct {     AdjList adjList;      int numVertexes, numEdges;  /* 图中当前顶点数和边数 */ } graphAdjList, *GraphAdjList; /* 邻接表的广度遍历算法 */ void BFSTraverse(GraphAdjList GL) {      int i, j;     EdgeNode *p;     Queue Q;      for (i =  0; i < GL->numVertexes; i++)         visited[i] =  false;     InitQueue(&Q); /* 初始化一辅助用的队列 */      for (i =  0; i < GL->numVertexes; i++) /* 对每一个顶点做循环 */     {          if (!visited[i]) /* 若是未访问过就处理 */         {             visited[i] =  true; /* 设置当前顶点访问过 */             cout << GL->adjList[i].data <<  ' ';  /* 打印顶点，也可以其它操作 */             EnQueue(&Q, i); /* 将此顶点入队列 */              while (!QueueEmpty(Q)) /* 若当前队列不为空 */             {                 DeQueue(&Q, &i); /* 将队对元素出队列，赋值给i */                 p = GL->adjList[i].firstedge; /* 找到当前顶点的边表链表头指针 */                  while (p)                 {                      /* 判断其它顶点若与当前顶点存在边且未访问过  */                      if (!visited[p->adjvex])                     {                         visited[p->adjvex] =  true; /* 将找到的此顶点标记为已访问 */                         cout << GL->adjList[p->adjvex].data <<  ' ';  /* 打印顶点 */                         EnQueue(&Q, p->adjvex); /* 将找到的此顶点入队列  */                     }                     p  = p->next; /* 指针指向下一个邻接点 */                 }             }         }     } }

遍历结果为：A F B G E I C H D (上图所示的图结构）

由结果可以看出，因为我们采用了不同的存储方式，即使使用的是同样的广度优先搜索，遍历的结果也是不同的。