二、开地址法
基本思想:当关键码key的哈希地址H0 = hash(key)出现冲突时,以H0为基础,产生另一个哈希地址H1 ,如果H1仍然冲突,再以H0
为基础,产生另一个哈希地址H2 ,…,直到找出一个不冲突的哈希地址Hi ,将相应元素存入其中。这种方法有一个通用的再散列函
数形式:
其中H0 为hash(key) ,m为表长,di称为增量序列。增量序列的取值方式不同,相应的再散列方式也不同。主要有以下四种:
线性探测再散列
二次探测再散列
伪随机探测再散列
双散列法
(一)、线性探测再散列
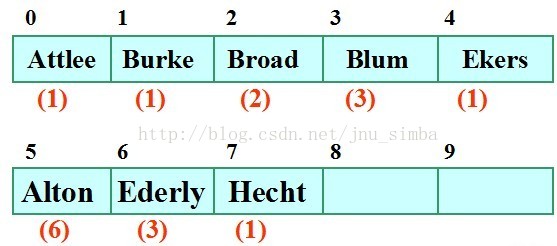
假设给出一组表项,它们的关键码为 Burke, Ekers, Broad, Blum, Attlee, Alton, Hecht, Ederly。采用的散列函数是:取其第一个字母在
字母表中的位置。
hash (x) = ord (x) - ord (‘A’)
这样,可得
hash (Burke) = 1hash (Ekers) = 4
hash (Broad) = 1hash (Blum) = 1
hash (Attlee) = 0hash (Hecht) = 7
hash (Alton) = 0hash (Ederly) = 4
又设散列表为HT[26],m = 26。采用线性探查法处理溢出,则上述关键码在散列表中散列位置如图所示。红色括号内的数字表示找
到空桶时的探测次数。比如轮到放置Blum 的时候,探测位置1,被占据,接着向下探测位置2还是不行,最后放置在位置3,总的探
测次数是3。
堆积现象
散列地址不同的结点争夺同一个后继散列地址的现象称为堆积(Clustering),比如ALton 本来位置是0,直到探测了6次才找到合适位
置5。这将造成不是同义词的结点也处在同一个探测序列中,从而增加了探测序列长度,即增加了查找时间。若散列函数不好、或装
填因子a 过大,都会使堆积现象加剧。
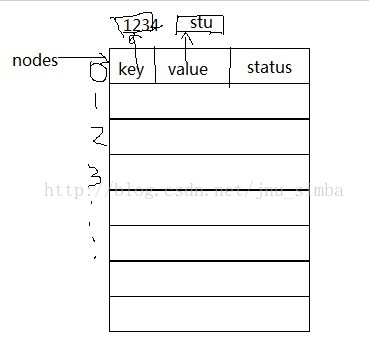
下面给出具体的实现代码,大体跟前面讲过的链地址法差异不大,只是利用的结构不同,如下:
status 保存状态,有EMPTY, DELETED, ACTIVE,删除的时候只是逻辑删除,即将状态置为DELETED,当插入新的key 时,只要不
是ACTIVE 的位置都是可以放入,如果是DELETED位置,需要将原来元素先释放free掉,再插入。
common.h:
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
#ifndef _COMMON_H_
#define _COMMON_H_ #include <unistd.h> #include <sys/types.h> #include <stdlib.h> #include <stdio.h> |








 本文介绍了开地址法处理散列冲突的基本思想,并重点讲解了线性探测再散列的方法,包括其工作原理、示例及堆积现象。通过实例展示了在散列表中如何应用线性探测再散列解决冲突,并提供了具体的C语言实现代码。
本文介绍了开地址法处理散列冲突的基本思想,并重点讲解了线性探测再散列的方法,包括其工作原理、示例及堆积现象。通过实例展示了在散列表中如何应用线性探测再散列解决冲突,并提供了具体的C语言实现代码。
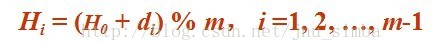

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 6048
6048

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








