聚类算法实现与分析

聚类算法实现与分析

机器学习的常用方法，主要分为有监督学习和无监督学习。监督学习，就是人们常说的分类，通过已有的训练样本（即已知数据以及其对应的输出）去训练得到一个最优模型（这个模型属于某个函数的集合，最优则表示在某个评价准则下是最佳的），再利用这个模型将所有的输入映射为相应的输出，对输出进行简单的判断从而实现分类的目的，也就具有了对未知数据进行分类的能力。

监督学习里典型的例子就是KNN、SVM。无监督学习也叫非监督学习则是另一种研究的比较多的学习方法，它与监督学习的不同之处，在于我们事先没有任何训练样本，而需要直接对数据进行建模。这听起来似乎有点不可思议，但是在我们自身认识世界的过程中很多处都用到了无监督学习。比如我们去参观一个画展，我们完全对艺术一无所知，但是欣赏完多幅作品之后，我们也能把它们分成不同的派别。无监督学习里典型的例子就是聚类了。聚类的目的在于把相似的东西聚在一起，而我们并不关心这一类是什么。因此，一个聚类算法通常只需要知道如何计算相似度就可以开始工作了。在这里实践了k-means,Hierarchical Clustering,Spectrum Clustering,并给出了各种聚类算的分析。

k-means聚类算法

聚类的方法有很多种，k-means数最简单的一种聚类方法了，其大致思想就是把数据分为多个堆，每个堆就是一类。每个堆都有一个聚类中心（学习的结果就是获得这k个聚类中心），这个中心就是这个类中所有数据的均值，而这个堆中所有的点到该类的聚类中心都小于到其他类的聚类中心（分类的过程就是将未知数据对这k个聚类中心进行比较的过程，离谁近就是谁）。其实k-means算的上最直观、最方便理解的一种聚类方式了，原则就是把最像的数据分在一起，而“像”这个定义由我们来完成，比如说欧式距离的最小，等等。

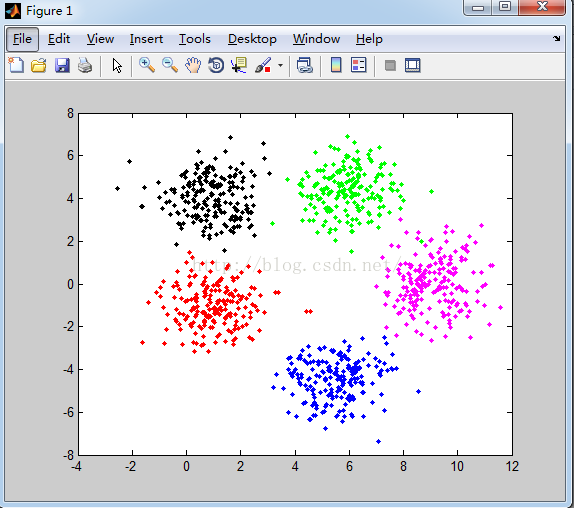
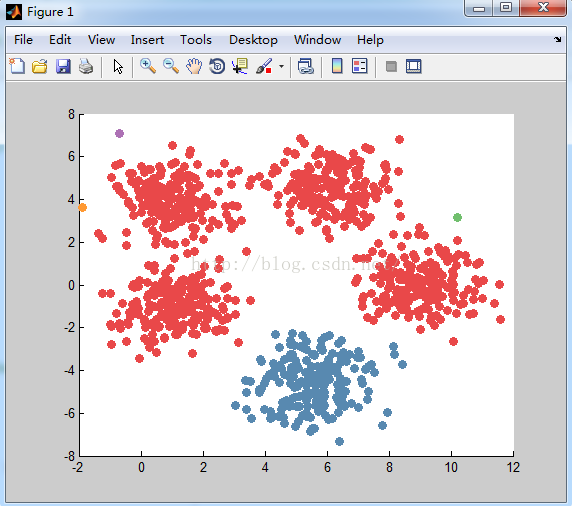
对数据1聚类

算法实现：

（1）   产生数据：

clc,clear

Sigma = [1, 0; 0, 1];

mu1 = [1, -1];

x1 = mvnrnd(mu1, Sigma, 200);

mu2 = [5.5, -4.5];

x2 = mvnrnd(mu2, Sigma, 200);

mu3 = [1, 4];

x3 = mvnrnd(mu3, Sigma, 200);

mu4 = [6, 4.5];

x4 = mvnrnd(mu4, Sigma, 200);

mu5 = [9, 0.0];

x5 = mvnrnd(mu5, Sigma, 200);

% obtain the 1000 data points to be clustered

X = [x1; x2; x3; x4; x5];

% Show the data point

plot(x1(:,1), x1(:,2), 'r.'); hold on;

plot(x2(:,1), x2(:,2), 'b.');

plot(x3(:,1), x3(:,2), 'k.');

plot(x4(:,1), x4(:,2), 'g.');

plot(x5(:,1), x5(:,2), 'm.');

save  X;

 

（2）k-means 聚类

clc;

n = size(X,1);

k=5;

rk = randperm(n);

Means = X(rk(1:k),:);

clusterID = zeros(n,1);

oldclusterID=clusterID;

while true

    oldclusterID=clusterID;

    Dist = pdist2(X,Means);

    [y,clusterID] = min(Dist,[],2);

    for i=1:k

        id = find(clusterID==i);

        Means(i,:) = mean(X(id,:));

    end

    if oldclusterID==clusterID

        break;

    end

end

id = find(clusterID==1);

figure;

plot(X(id,1),X(id,2),'r.'); hold on;

id = find(clusterID==2);

plot(X(id,1),X(id,2),'b.');

id = find(clusterID==3);

plot(X(id,1),X(id,2),'k.');

id = find(clusterID==4);

plot(X(id,1),X(id,2),'g.');

id = find(clusterID==5);

plot(X(id,1),X(id,2),'m.');

设置聚类中心为5个，得到如下的聚类结果：

分析：

       产生的数据说明：每个类别产生的数据都是服从正太分布，且均值不同但方差矩阵相同。

       分类结果：从k-means分类的结果可以看到，k-means对这类数据分类的准确度相对很高。在每一类的边缘可能存在错分样本，在每个类别中间部分分类准确度想当高。

 

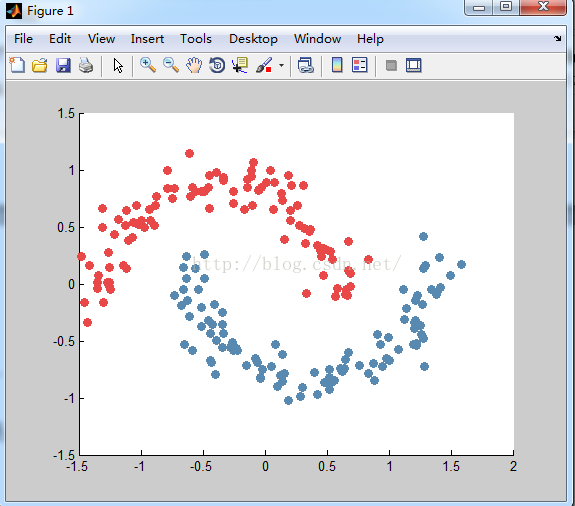
对数据2聚类

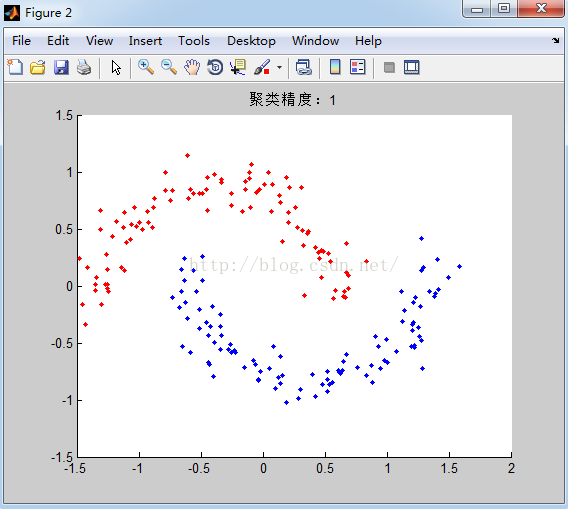
原始数据图：

聚类后结果：设置聚类类别数为2.

分析：

       产生的数据说明：产生的数据是流型的数据。

       分类结果：从k-means分类的结果可以看到，k-means对流型数据分类的准确度较差。

 

k-means方法总结：

算法优点：

       1．算法快速、简单;

2．对大数据集有较高的效率并且是可伸缩性的;

3．时间复杂度近于线性，而且适合挖掘大规模数据集。K-Means聚类算法的时间复杂度是O(nkt) ,其中n代表数据集中对象的数量，t代表着算法迭代的次数，k代表着簇的数目。

算法缺点：

1.     在 K-means 算法中 K 是事先给定的，这个 K 值的选定是非常难以估计的。很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。这也是 K-means 算法的一个不足。有的算法是通过类的自动合并和分裂，得到较为合理的类型数目 K，例如 ISODATA 算法。关于 K-means 算法中聚类数目K 值的确定在文献中，是根据方差分析理论，应用混合 F统计量来确定最佳分类数，并应用了模糊划分熵来验证最佳分类数的正确性。

2.     在 K-means 算法中，首先需要根据初始聚类中心来确定一个初始划分，然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响，一旦初始值选择的不好，可能无法得到有效的聚类结果，这也成为 K-means算法的一个主要问题。

3.     从 K-means 算法框架可以看出，该算法需要不断地进行样本分类调整，不断地计算调整后的新的聚类中心，因此当数据量非常大时，算法的时间开销是非常大的。所以需要对算法的时间复杂度进行分析、改进，提高算法应用范围。

层次聚类Hierarchical Clustering

       整个聚类过程其实是建立了一棵树，在建立的过程中，可以通过在第二步上设置一个阈值，当最近的两个类的距离大于这个阈值，则认为迭代可以终止。另外关键的一步就是第三步，如何判断两个类之间的相似度有不少种方法。这里介绍一下三种：

       SingleLinkage：又叫做 nearest-neighbor，就是取两个类中距离最近的两个样本的距离作为这两个集合的距离，也就是说，最近两个样本之间的距离越小，这两个类之间的相似度就越大。容易造成一种叫做 Chaining 的效果，两个 cluster 明明从“大局”上离得比较远，但是由于其中个别的点距离比较近就被合并了，并且这样合并之后 Chaining 效应会进一步扩大，最后会得到比较松散的 cluster 。

      CompleteLinkage：这个则完全是 Single Linkage 的反面极端，取两个集合中距离最远的两个点的距离作为两个集合的距离。其效果也是刚好相反的，限制非常大，两个 cluster 即使已经很接近了，但是只要有不配合的点存在，就顽固到底，老死不相合并，也是不太好的办法。这两种相似度的定义方法的共同问题就是指考虑了某个有特点的数据，而没有考虑类内数据的整体特点。

      Average-linkage：这种方法就是把两个集合中的点两两的距离全部放在一起求一个平均值，相对也能得到合适一点的结果。

      average-linkage的一个变种就是取两两距离的中值，与取均值相比更加能够解除个别偏离样本对结果的干扰。

算法实现：

xx=X;

[number, row]=size(xx); 

yy=pdist(xx,'euclidean'); 

zz=linkage(yy,'single'); 

Ncluster = 2;

c = cluster( zz,'maxclust', Ncluster );

if(Ncluster>12) 

 Color = linspecer( Ncluster ); 

 else 

     Color = linspecer( Ncluster, 'qualitative' ); 

     end

for i=1:Ncluster 

     for j = 1:number 

     if(c(j) == i)     

     hold on    plot(xx(j,1),xx(j,2),'o','MarkerFaceColor',Color(i,:),'MarkerEdgeColor',Color(i,:)) 

     end 

     end 

 end 

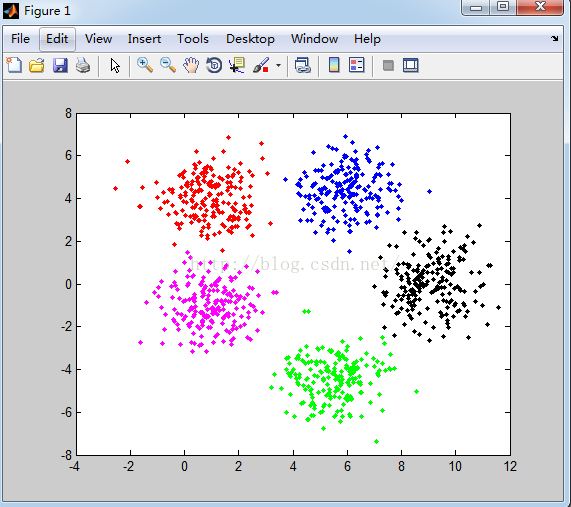
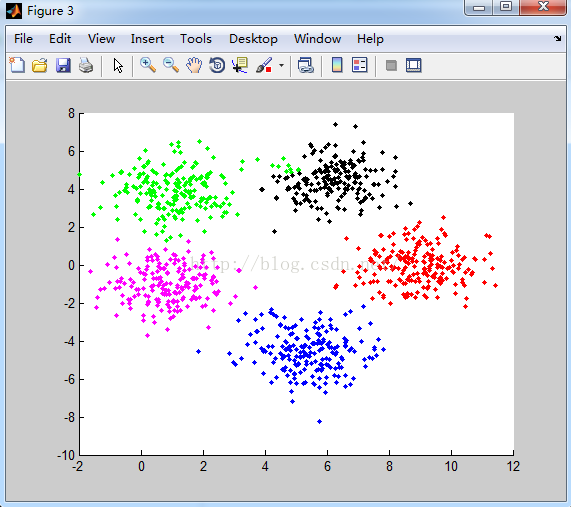
对数据1聚类后结果：

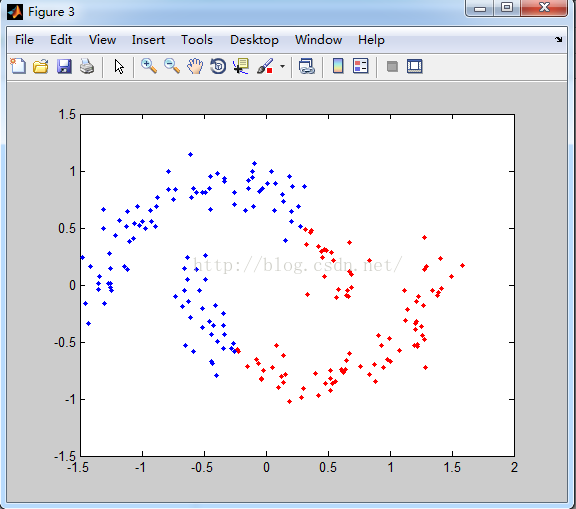
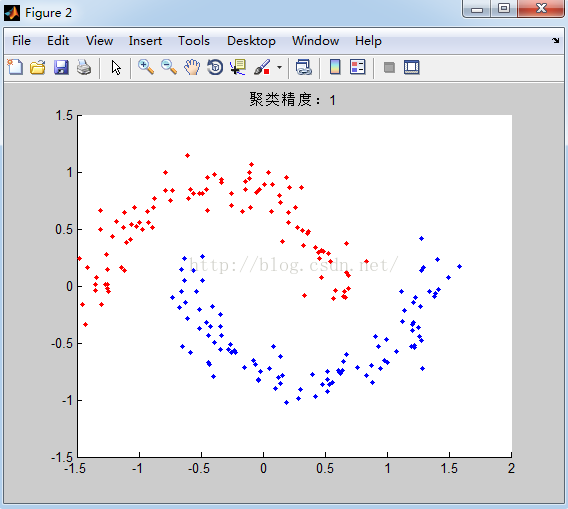
对数据2聚类后结果：

结果分析：

       数据1使用的是每个类别产生的数据都是服从正太分布，且均值不同但方差矩阵相同。  数据2使用的是流型的数据。

       可以看到Hierarchical Clustering对数据1 的聚类结果相当不理想，Hierarchical Clustering把外点当做一个单独的类别。但是HierarchicalClustering对数据2的聚类想多相当好，基本上把每个类别的数据都划分到了各自的类别。

 

HierarchicalClustering算法总结：

算法优点：

1．距离和规则的相似度容易定义，限制少；

2．不需要预先制定聚类数；

3．可以发现类的层次关系；

4．可以聚类成其它形状；

算法缺点:

1．计算复杂度太高；

2．奇异值也能产生很大影响，从Hierarchical Clustering对数据1的分类可以看到，奇异值对该算法的影响相当大，对分类的结果起到决定性的作用；

3．算法很可能聚类成链状，从Hierarchical Clustering对数据2的分类可以看到，该算法可以聚类成链状，且数据本省也是链状，但是对于其他的数据，分类成链状可能就不适合；

 

谱聚类Spectrum Clustering

         谱聚类是一种基于图论的聚类方法——将带权无向图划分为两个或两个以上的最优子图，使子图内部尽量相似，而子图间距离尽量距离较远，以达到常见的聚类的目的。其中的最优是指最优目标函数不同，可以是割边最小分割,也可以是分割规模差不多且割边最小的分割。

       谱聚类算法首先根据给定的样本数据集定义一个描述成对数据点相似度的亲合矩阵,并且计算矩阵的特征值和特征向量 ， 然后选择合适 的特征向量聚类不同的数据点。谱聚类算法最初用于计算机视觉 、VLS I 设计等领域， 最近才开始用于机器学习中，并迅速成为国际上机器学习领域的研究热点。谱聚类算法建立在谱图理论基础上，其本质是将聚类问题转化为图的最优划分问题，是一种点对聚类算法，与传统的聚类算法相比，它具有能在任意形状的样本空间上聚类且收敛于全局最优解的优点。

聚类算法实现：

 

length=size(X,1);

 

k=5;

 

sigma = 2;

W = zeros(length,length);

classify_num=5;

for i=1:1:length

    [joint,weights] = KNN(X,k,i,sigma);

    for j =1:1:k

        W(i,joint(j)) = weights(j);

        W(joint(j),i) =weights(j);

    end

end

 

degs = sum(W, 2);

D = sparse(1:size(W, 1),1:size(W, 2), degs);

L = D - W;

[Q, V] = eigs(L, k, 'SA');

C = kmeans(Q, classify_num);

figure ,hold on

for i=1:1:length

    if C(i,1)==1

        plot(X(i,1),X(i,2),'r.')

    elseif C(i,1)==2

        plot(X(i,1),X(i,2),'g.')

    elseif C(i,1)==3

        plot(X(i,1),X(i,2),'k.')

    elseif C(i,1)==4

        plot(X(i,1),X(i,2),'b.')

    elseif C(i,1)==5

        plot(X(i,1),X(i,2),'m.')

    end

end

对数据1聚类结果：

 

对数据2聚类结果

 

谱聚类算法

根据不同的图拉普拉斯构造方法，可以得到不同的谱聚类算法形式。 但是，这些算法的核心步骤都是相同的：

（1）利用点对之间的相似性，构建亲和度矩阵；

（2）构建拉普拉斯矩阵；

（3）求解拉普拉斯矩阵最小的特征值对应的特征向量（通常舍弃零特征所对应的分量全相等的特征向量）；

（4）由这些特征向量构成样本点的新特征，采用K-means等聚类方法完成最后的聚类。

 

谱聚类算法分析：

算法优点：

1．和 K-medoids 类似，Spectral Clustering 只需要数据之间的相似度矩阵就可以了，而不必像 K-means 那样要求数据必须是 N 维欧氏空间中的向量。

2．由于抓住了主要矛盾，忽略了次要的东西，因此比传统的聚类算法更加健壮一些，对于不规则的误差数据不是那么敏感，而且 performance 也要好一些。许多实验都证明了这一点。事实上，在各种现代聚类算法的比较中，K-means 通常都是作为 baseline 而存在的。

3．计算复杂度比 K-means 要小，特别是在像文本数据或者平凡的图像数据这样维度非常高的数据上运行的时候。

算法挑战：

1．可伸缩性。可伸缩性是指聚类算法无论对于小数据集还是大数据集，都应该是有效的；无论是对于小类别数据还是具有大别类数目的数据，都应该是有效的。

2．具有不同类型的数据处理能力。可处理数值型数据，也可处理非数㨁型数据；既可处理离散数据，也可处理连续域内的数据。比如布尔型、时序型、枚举型、以及这些类型的混合。

3．能够发现任意形状的聚类。能够发现任意形状的簇，球状的、位于同一流形上的数据。因此，选择合适的距离试题很关键。构造相似度矩阵。如何创建相似度矩阵，使其更加真实地反映数据点之间的近似关系，使得相近点之间的相似度更高，相异点之间的相似度更低，是谱聚类算法必须要解决的一个问题。高斯相似函数是经典谱聚类算法中计算两点间相似度的常用方法，虽然该函数使原始的谱聚类算法取得了一些成功，但尺度参数σ的选取问题使该函数具有明显的局限性。

4．自动确定聚类数目。由相似度矩阵得到拉普拉斯矩阵后，接下来要确定所需特征向量的数目，它与最终的聚类数目相等。虽然该数目可以由人工确定，但是准确地给出对聚类效率和最终的聚类质量有直接影响的数目值是个非常困难的问题。因此，如何自动确定聚类数目成为谱聚类需要解决的关键问题之一。

5．谱聚类的运行速度。在谱聚类算法的聚类过程中需要求解矩阵的特征值与特征向量，求解非稀疏矩阵特征向量的复杂度O(n)，所以处理大规模数据集的时候，计算中形成的矩阵空间非常大，求解过程不但会非常耗时，而且所需要的内存空间也非常大，面临着内存溢出的危险，对计算机内存容量的要求变得较高。因此，如何提高算法的运行速度，降低运行所需的内存空间，减少算法运行的时间和空间代价是谱聚类算法在不断扩展应用领域的过程中所面临的另一关键问题。

 

附件：

数据1：每个类别产生的数据都是服从正太分布，且均值不同但方差矩阵相同.

clc,clear

Sigma = [1, 0; 0, 1];

mu1 = [1, -1];

x1 = mvnrnd(mu1, Sigma, 200);

mu2 = [5.5, -4.5];

x2 = mvnrnd(mu2, Sigma, 200);

mu3 = [1, 4];

x3 = mvnrnd(mu3, Sigma, 200);

mu4 = [6, 4.5];

x4 = mvnrnd(mu4, Sigma, 200);

mu5 = [9, 0.0];

x5 = mvnrnd(mu5, Sigma, 200);

% obtain the 1000 datapoints to be clustered

X = [x1; x2; x3; x4; x5];

% Show the data point

plot(x1(:,1), x1(:,2), 'r.'); hold on;

plot(x2(:,1), x2(:,2), 'b.');

plot(x3(:,1), x3(:,2), 'k.');

plot(x4(:,1), x4(:,2), 'g.');

plot(x5(:,1), x5(:,2), 'm.');

save  X;

 

数据2：产生流型数据

X = [-1.3046 -0.1606

-1.4341 -0.3372

-1.3475 -0.0421

-1.3426 0.0746

-1.2433 -0.0451

-1.3477 0.0140

-1.2695 0.0159

-1.2560 -0.0217

-1.4525 -0.1600

-1.4813 0.2405

-1.2533 0.1410

-1.1160 0.1336

-1.2506 0.0134

-1.4179 0.1585

-1.1427 0.1662

-1.2654 0.2749

-1.3093 0.4972

-0.8894 0.5117

-1.2147 0.4365

-1.0589 0.5416

-1.0974 0.3831

-1.1807 0.5650

-1.0185 0.5226

-1.1234 0.5162

-0.9260 0.5602

-1.1131 0.6486

-1.0704 0.4117

-1.3090 0.6600

-0.9298 0.6564

-0.7473 0.7469

-0.8765 0.7687

-1.0327 0.6897

-0.8800 0.6879

-0.7897 0.8371

-0.9968 0.5561

-0.7329 0.8403

-0.9754 0.4914

-0.5870 0.8492

-0.7836 0.9945

-0.5976 0.7718

-0.6082 1.1435

-0.5593 0.8088

-0.4512 0.6593

-0.4470 0.9503

-0.5153 0.8144

-0.4882 0.8137

-0.3907 0.9800

-0.3310 0.9054

-0.4595 0.8447

-0.2568 0.8148

-0.1615 0.6493

-0.1068 0.9994

-0.3376 0.9333

-0.0439 0.8333

-0.0312 0.8441

-0.1402 0.8472

-0.0961 1.0671

0.0436 0.9985

-0.2503 0.7038

-0.1422 0.9170

-0.1054 0.9390

-0.0536 0.8220

0.3137 0.8682

0.0720 0.6508

0.0782 0.8938

-0.0973 0.6904

0.1411 0.7367

0.1296 0.7934

0.2079 0.5609

0.2143 0.8637

0.0133 0.8896

0.2598 0.6927

0.1868 0.9497

0.1563 0.3887

0.2798 0.5154

0.2081 0.6446

0.3619 0.4604

0.4530 0.2400

0.3655 0.4805

0.4878 0.3051

0.3224 0.4864

0.4199 0.3399

0.4536 0.2371

0.4703 0.3144

0.3250 0.3584

0.4466 0.2982

0.6724 0.3708

0.5432 0.2119

0.6769 0.1165

0.5262 0.2860

0.8319 0.2159

0.6931 -0.0227

0.3347 -0.0805

0.6928 0.0936

0.4681 0.0717

0.6455 -0.0896

0.6603 -0.0498

0.6617 -0.1023

0.5885 -0.0414

0.5709 -0.1069

-0.5597 0.1367

-0.6311 0.2434

-0.4894 0.0448

-0.6578 0.1441

-0.4873 0.2604

-0.5392 -0.0516

-0.6547 -0.0502

-0.6288 -0.1486

-0.7275 -0.1015

-0.6298 0.0501

-0.3436 -0.2539

-0.6768 -0.1921

-0.6052 -0.2849

-0.4088 -0.1798

-0.5129 -0.2064

-0.3433 -0.3513

-0.5111 -0.3768

-0.4578 -0.3235

-0.3441 -0.5589

-0.4199 -0.3592

-0.3887 -0.4941

-0.6470 -0.5287

-0.4376 -0.4311

-0.2540 -0.5804

-0.5833 -0.5855

-0.2180 -0.5837

-0.3327 -0.4320

-0.4364 -0.6702

-0.4299 -0.6884

-0.4017 -0.7903

-0.2743 -0.5594

-0.2300 -0.5676

-0.0773 -0.6538

-0.0194 -0.7473

-0.1527 -0.7179

-0.2595 -0.5159

-0.0402 -0.8188

0.1271 -0.7987

0.0809 -0.5309

0.1404 -0.8573

0.1402 -0.6199

-0.0565 -0.6858

0.0977 -0.8960

0.1566 -0.7853

0.2867 -0.9838

0.1906 -1.0191

0.0526 -0.7277

-0.0401 -0.8271

0.3977 -0.7768

0.5240 -0.9277

0.3055 -0.9099

0.5350 -0.8659

0.5637 -0.8476

0.4200 -0.9719

0.5199 -0.7543

0.6421 -0.7453

0.6160 -0.7585

0.4763 -0.8627

0.5213 -0.8194

0.6220 -0.7689

0.6079 -0.7382

0.8823 -0.8498

0.6742 -0.6028

1.0800 -0.5724

0.7631 -0.7106

0.8309 -0.7879

0.9476 -0.7258

0.6503 -0.6596

0.9792 -0.6558

0.9327 -0.5266

0.9087 -0.4398

1.2249 -0.5257

1.0020 -0.6705

0.8749 -0.6966

0.9947 -0.4664

1.2899 -0.7225

1.2173 -0.3204

1.1954 -0.5276

1.2815 -0.4800

1.2609 -0.4442

1.2198 -0.5365

1.2043 -0.3410

1.2503 -0.3602

1.2035 -0.3879

1.3811 -0.0959

1.2714 -0.1807

1.4145 -0.0326

1.1280 -0.3075

1.3946 -0.0686

1.1405 -0.2190

1.2109 -0.1448

1.4998 0.0787

1.1156 -0.0481

1.5878 0.1745

1.2817 0.4193

1.3417 -0.0501

1.2290 -0.1015

1.4039 0.2343

1.2912 0.1612

1.2759 0.1342];