拉格朗日乘子法、罚函数法、乘子罚函数法

本文简单总结一些相关概念，具体证明以后再补充；
1. 拉格朗日乘子法
2. 罚函数法：外罚函数与内罚函数法
3. 广义乘子法

1. 拉格朗日乘子法

1.1 无约束问题

无约束问题，定义为 $\min f(x)$， 对于凸函数而言，直接利用费马定理，$f^{'}(x)=0$，获得最优解；

1.2 等式约束问题

等式约束定义如下：

$$\min f(x)\\ s.t. g(x)=0$$
现在利用拉格朗日乘子法，合并式子：
$$L(x,a)=f(x)+ag(x)$$
对 $x,a$分别求偏导：
$$\nabla_{x} L(x,a)=f^{'}(x)+ag^{'}(x)=0 \\ \nabla_{a} L(x,a)=g(x)=0$$
发现第二个式子刚好是其约束条件；

为什么？
现在，我们在平面内投影函数，画出$f(x)$的等高线，以及$g(x)=0$的边界线；如图示：
蓝色虚线代表了$f(x,y)$的等高线；红色代表$g(x,y)=c=0$;

回顾：
1. 方向导数是各个方向上的导数
2. 偏导数连续才有梯度存在
3. 梯度的方向是方向导数中取到最大值的方向，梯度的值是方向导数的最大值(垂直方向)
假设$f(x)$的最小值在圆心处，即梯度方向向外；$g(x,y)$的梯度方向向下；
那么满足条件的值一定是两个函数相切处；如果相交，那么一定还存在一个等高线与红线相切，而且更小；在切点处，两个函数的梯度共线，即$f^{'}(x)=-ag'(x),a<0$；做简单的变换后：$f'(x)+ag'(x)=0$，这就是第一个等式啦，同时还需要满足第二个式子；

1.3 不等式约束问题（KKT条件）

不等式约束问题：

$$\min f(x) \\ s.t. g(x)=0 \\ h(x)<=0$$
引入拉格朗日函数：(KTT 条件)
$$L(x,a,b)=f(x)+ag(x)+bh(x)\\ s.t. g(x)=0 \\ bh(x)=0$$
这样就将不等式约束变成了等式约束，偏导等于零即可求得最优参数；
$$\min f(x) 等价于 \min_x \max_{a,b} L(x,a,b)$$
对偶变换后有： $$\max_{a,b} \min L(x,a,b)$$
因为 $h(x)<0$，所以只有当 $bh(x)=0$时， $L(x,a,b)$才能取得最大值；否则不满足条件；所以KKT条件是 $\min f(x)$的必要条件；

补充：SVM 满足KKT条件:在边界上的点，有$h(x)=0$；非边界处，令b=0;

1.4 拉格朗日乘子法问题

当 目标函数的Hess矩阵不正定时（特征值不全为正，或者行列式不为正，那么此时的偏导为0处，并不能确定是否是极值点），所以无法求解；

例子：
求解

$$\begin{equation}\begin{cases} \min f=2x^2+y^2-2xy \\s.t. x+y=1 \end{cases} \end{equation}$$
我们定义 $L(x,y,\lambda)=f-\lambda g(x)=2x^2+y^2-2xy-\lambda(x+y-1)$
求偏导可得： $$\begin{cases} \frac{\partial L}{\partial x}=4x-2y-\lambda=0 \\\frac{\partial L}{\partial y}=2y-2x-\lambda=0 \\ \frac{\partial L}{\partial \lambda}=x-y-1=0 \end{cases}$$
我们可以计算原目标函数的Hess矩阵： $\mathcal A=\begin{bmatrix} \frac{\partial ^2L}{\partial x^2} & \frac{\partial ^2L}{\partial x \partial y} \\ \frac{\partial ^2L}{\partial y \partial x} & \frac{\partial ^2L}{\partial y^2} \end{bmatrix}=\begin{bmatrix} 4 & -2 \\ -2 & 2\end{bmatrix}$正定矩阵；
再看一个目标函数，方程稍作修改：
$$\left \{\begin{array}{cc} \min f=2x^2+y^2+3xy \\s.t. x+y=1 \end{array}\right.$$
直接求偏导，发现方程无解；
再看其Hess矩阵： $\mathcal B =\begin{bmatrix}4 &3 \\3 &2 \end{bmatrix}$非正定矩阵；
也就是说，在梯度为零处，我们无法判断是否是极值；

---

2. 罚函数法

2.1 定义

罚函数法：根据约束条件的特点，构造出惩罚函数，然后加入到目标函数中，将其转化为无约束问题；新目标函数的解与原始目标函数解一致；

2.1.1 等式约束的罚函数法：

$$\left \{\begin{array}{cc}\min f(x) \\s.t. g_i(x)=0 \end{array} \right .$$
我们引入一个增广目标函数：
$$\min F(x,\sigma)=f(x)+\sigma P(x)\\ P(x)=g^Tg$$
这里： $\sigma$是惩罚因子，取很大的正数， $F(x,\sigma)$是罚函数， $\sigma P(x)$是惩罚项；
惩罚项的性质：
1. 当$x$为可行解时，$P(x)=0$，惩罚项为0；
2.当$x$不在可行域内，此时$\sigma P(x)$会很大，那么求得$\min F(x,\sigma)$必然有$\min f(x)$与$\min_{x,\sigma}[\sigma P(x)]$同时成立；所以，当$\sigma$充分大时，增广目标函数的最优值接近于原始问题的最优值；（$\sigma \rightarrow \infty$，若原问题有解（$F<\infty$），则会有$g=0$）

例如：

$$\min f(x)=(x_1+x_2)^2 \\s.t. g(x)=x_1+x_2 =c$$
构造罚函数为： $$\min L(x,\sigma)=\min f(x)+\sigma||g(x)||_2^{2}$$
$\sigma$设置的值较大；第一部分优化解，第二部分使得解在可行域内；
如果x不在可行域内，需要我们大步迭代；

2.1.2 不等式约束的罚函数法：

$$\left \{\begin{array}{cc}\min f(x) \\s.t. h_i(x)>=0 \end{array} \right .$$
此时我们构造惩罚项；
（1） $P(x)=\sum \left [\min(0,h_i(x))\right]^2$，可以简单分析出：当 $h_i(x)>=0$时 $P(x)=0$，满足条件；当不在可行域内时，我们需要加大惩罚；
（2） $P(x)=\sum \alpha_i h_i^2$,其中 $\alpha_i = \begin{cases} 0, h_i>=0 \\1, h_i< 0 \end{cases}$

2.1.3 一般形式的罚函数法：

$$\begin{cases} \min f(x) \\s.t. \\ g_i(x)=0 \\h_i(x)>=0 \end{cases}$$
那么罚函数为： $$P(x)=\sum [g_i(x)]^2 + \sum[min(0,h_i(x))]^2$$

特别注意：惩罚因子是充分大的数，拉格朗日乘子是一个确定的参数，意义不一样；(当惩罚因子过大时，在求解极小值的过程中，Hess矩阵变成病态矩阵？)

2.2 外罚函数法

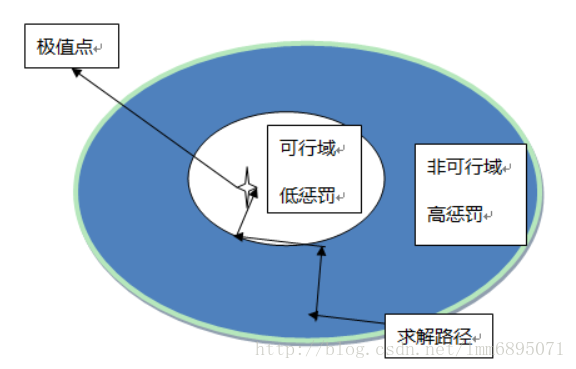
对不在可行域内，加大惩罚；上文介绍的就是外罚函数法；

2.3 内罚函数法

又称障碍函数法，内点法）；在可行域内筑起高墙，迫使值在可行域内，目标函数无法穿越；（只适用于不等式约束）
障碍函数一般取：（1）倒数 （2）对数
障碍因子为很小的正数
当$x$趋于边界时，那么障碍函数趋于无穷；初始点在可行域内部；
在可行域内时，障碍函数值很小，增广目标函数与原始目标函数等价了；

---

3. 广义乘子法

3.1 等式约束广义乘子法：

$$\begin{cases}\min f(x) \\ s.t. g_i(x)=0 \end{cases}$$
广义乘子法是拉格朗日乘子法与罚函数法的结合；

$$\phi(x,\lambda,\sigma)=f(x)+\lambda^T g(x)+\frac{1}{2}\sigma g^T(x)g(x)$$
在罚函数的基础上增加了乘子项，首先在 $\sigma$足够大的基础上，获得 $\phi$的极小值，然后在调整 $\lambda$获得原问题的最优解；
迭代公式如下：
梯度等于零： $\nabla_x \phi(x_k,\lambda_k,\sigma_k)=0$,即 $$\nabla_xf(x_k)+\lambda_k \nabla_x g^T(x_k)+\sigma_k \nabla_x g^T(x_k)g(x_k)\\= \nabla_xf(x_k)+\nabla_x g^T(x_k)(\sigma_k g(x_k)+\lambda_k)=0$$
令 $\lambda_{k+1}=\sigma_k g(x_k)+\lambda_k$，则导出拉格朗日乘子法的一阶必要条件；
$$\nabla_x f(x_k)+\lambda_{k+1}\nabla g=0$$
计算方法：
(1)初始值设置： $x,\lambda,\sigma$
(2)计算梯度为0，获得当前最优值 $x_k$，然后判断是否终止；
(3)是否调整惩罚因子，获得 $\sigma_{k+1}$
(4)计算 $\lambda_{k+1}=\sigma_k g(x_k)+\lambda_k$

3.2 不等式约束广义乘子法：

思想是：引入松弛变量，化不等式问题为等式约束；

$$\begin{cases}\min f(x) \\ s.t. h_i(x)>=0 \end{cases} \rightarrow \begin{cases}\min f(x) \\ s.t. h_i(x)=\beta_i \end{cases}$$
那么原始问题转化成：
$$\min_{x,\lambda} \phi(x,\lambda,\sigma)=f(x)+\lambda^T (h(x)-\beta)+\frac{1}{2}\sigma (h(x)-\beta)^T(h(x)-\beta)\\ \min_{x,\lambda,\sigma,\beta } \phi(x,\lambda,\sigma,\beta)=f(x)+\frac{\sigma}{2}\left ((h+\frac{\lambda}{\sigma}-\beta )^2-(\frac{\lambda}{\sigma})^2\right) \\\beta=\frac{1}{\sigma} \max \{ 0,\sigma h+\lambda\}$$
首先计算关于 $\beta$的极小值；因为 $\beta>=0$，上式是关于 $\beta$的二次函数，开口向上，对称轴是 $h+\frac{\lambda}{\sigma}$， $$\beta=\begin{cases}0 &h+\frac{\lambda}{\sigma}<0 \\h+\frac{\lambda}{\sigma} & h+\frac{\lambda}{\sigma}>=0\end{cases} \rightarrow \frac{1}{\sigma}\max\{0,\sigma h+\lambda\}$$
这样做的目的是：保证增广目标函数最优解近似于原始问题最优解；
分析：当 $\sigma h +\lambda >=0$时， $\beta=h+\frac{\lambda}{\sigma}$，则 $$\phi(x,\lambda,\sigma)=f(x)-\frac{\sigma}{2}(\frac{\lambda}{\sigma})^2=f(x)-\frac{\lambda^2}{2 \sigma} \\\nabla_x \phi(x,\lambda,\sigma)=\nabla_x f(x)$$
当 $\sigma h +\lambda <0$时， $\beta=0$，则 $$\phi(x,\lambda,\sigma)=f(x)-\frac{\sigma}{2}(\frac{\lambda}{\sigma})^2+\frac{(\sigma h+\lambda)^2}{2\sigma}=f(x)-\frac{\lambda^2}{2 \sigma}+\frac{(\sigma h+\lambda)^2}{2\sigma} \\\nabla_x \phi(x,\lambda,\sigma)=\nabla_x f(x)+(\sigma h+\lambda)\nabla h(x)$$
梯度为零计算最优解，发现刚好满足朗格朗日乘子法的必要条件；

3.3 一般约束广义乘子法：

混合等式不等式约束法，计算即可。