Topic模型
概要:
LFM(依赖于矩阵分解)
LSA(LSI)(SVD分解)
PLSI(EM算法优化,频率学派,参数未知但固定)
LDA(在PLSA基础上加上贝叶斯框架, α , β ~dirichlet分布,分别作为主题-文档和词-主题的先验分布;贝叶斯学派的特点是参数是随机变化的,但是服从某个分布,不断的学习新的知识,形成后验)
介绍:
LFM、LSI、PLSI、LDA都是隐含语义分析技术,是同一类概念;在本质上是相通的,都是找出潜在的主题或特征。这些技术首先在文本挖掘领域中被提出来,近些年也被不断应用到其他领域中,并得到了不错的应用效果。
在推荐系统中它能够基于用户的行为对item进行自动聚类,也就是把item划分到不同类别/主题,这些主题/类别可以理解为用户的兴趣。对文本信息进行隐含主题发掘以提取必要特征,譬如LDA获得主题分布之后,可以实现对文档的降维。在论文推荐领域,次LDA+PMF模型实现协同主题回归模型(CTR)。
LFM (隐语义模型)
例子:
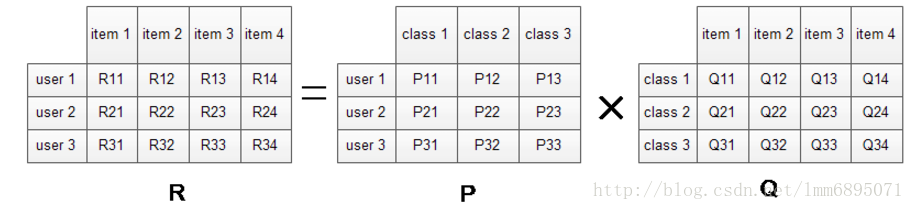
将用户评分矩阵(混淆矩阵)分解R=P* Q
P矩阵代表了 user-class
Q矩阵代表了class-item
class:根据自动聚类算法获得几个类标签;
P、Q中的参数通过模型学习得到:
最后计算平方损失函数,利用随机梯度下降法,使得损失值最小;
LSA模型
Latent Semantic Analysis (Latent Semantic Indexing)
背景
传统的信息检索中:将单词作为特征,构造特征向量;计算查询单词与文档间的相似度;但是没有考虑到语义、同义词等相关信息;在基于单词的检索方法中,同义词会降低检索算法的召回率(Recall),而多义词的存在会降低检索系统的准确率(Precision)。
我们希望找到一种模型,能够捕获到单词之间的相关性。如果两个单词之间有很强的相关性,那么当一个单词出现时,往往意味着另一个单词也应该出现(同义 词);反之,如果查询语句或者文档中的某个单词和其他单词的相关性都不大,那么这个词很可能表示的是另外一个意思(比如在讨论互联网的文章中,Apple 更可能指的是Apple公司,而不是水果) 。
LSA(LSI)使用SVD 来对单词-文档矩阵进行分解。 SVD 可以看作是从单词-文档矩阵中发现不相关的索引变量(因子),将原来的数据映射到语义空间内。在单词-文档矩阵中不相似的两个文档,可能在语义空间内比较相似。
SVD ,亦即奇异值分解 ,一个 t∗d 维的(单词-文档矩阵) X ,可以分解为:
还原后的X’与X差别很大,这是因为我们认为之前X存在很大的噪音,X’是对X处理过同义词和多义词后的结果。
在查询时,对与每个给定的查询q,我们根据这个查询中包含的单词( Xq )构造一个伪文档: Dq=XqTS−1 ,然后该伪文档和 D′ 中的每一行计算相似度(余弦相似度)来得到和给定查询最相似的文档。
下面介绍主题模型,PLSA,LDA;
这里需要介绍一部分基础知识:共轭分布,频率学派,贝叶斯学派;
频率学派思想: 参数未知,但是固定,可以通过样本,计算最大似然估计获得;
贝叶斯学派思想:参数未知,是个随机变量,但是服从某个分布;参数服从某个先验分布,然后我们通过现有数据修正模型,获得后验分布;
先验知识+数据知识 ———>后验分布;
共轭分布:先验分布的形式和后验分布的形式一样;
比如:先验是Beta分布,数据分布是伯努利分布(0-1分布),那么后验分布仍然是Beta分布;
Dirichlet分布+多项式分布=Dirichlet分布
PLSA模型
首先,回顾一元模型,然后引出贝叶斯学派的一元模型;

如图示:
一元模型中,不存在潜在主题,我们产生word的过程,相当于投骰子(V面);那么整个文档集的分布是:(文档直接独立,word之间独立)
p(W)=∏dD∏iNp(wi)=∏dD∏vVp(wv)cv
然后通过最大似然方法获得参数, p(wi)^=ciC , C 是总的頻数;
混合一元模型:
这里,我们假定,一篇文档有一个主题z,因此,
p(W,z|d)=p(z|d)∏iNp(wi|z)p(W|d)=∑zp(z|d)∏iNp(wi|z)
以上频率学派思想,现在,利用贝叶斯学派思想,重新思考模型:
现在有一个坛子,里面有无穷多个骰子(V面);现在,我们首先得抽取一个骰子,然后才能进行计算;我们假定选取过程是服从Dirichlet分布的(先验),因为我们知道,投骰子时,获得word的頻数是服从多项式分布的;这样后验概率也是Dirichlet分布;
这里先验参数是 θ ,那么
p(W,θ)=p(θ)p(W|θ)p(W)=∫p(θ)p(W|θ)dθ=∫p(θ)∏p(wi|θ)dθ
我们回顾了基础知识;现在我们来分析一下PLSA模型,概率图模型如图C所示;可以看到,每一篇文档含有多个主题;;
现在,我们生成文档的过程是:我们投骰子(K面,代表文档-主题概率)获得主题z,然后寻找到主题为z的那个主题-word骰子,然后投骰子获得word;
即:
这里可以使用EM算法,最大似然方法进行模型估计;
LDA模型
PLSA 模型本质上是频率学派思想,我们现在利用贝叶斯思想进行考虑;
引入Dirichlet先验, α,β 是Dirichlet分布的参数;
这样,先根据先验获得一个主题-文档分布的参数,然后从多项式分布得到一个主题,即 α∼θm∼zm,n ;
同时从 β 先验中,获得多项式分布,然后根据具体主题获得word,即: β∼ϕk∼wm,n|k=zm,n
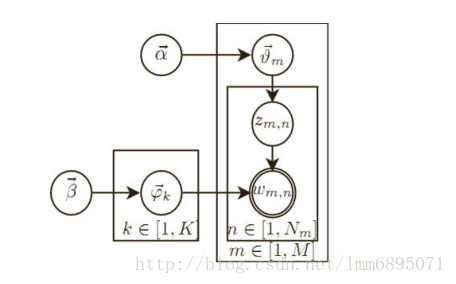
数据知识仍然是多项分布(词频);
这样的话,可以得到参数的后验概率: Dir(θm|nm+α)
所以topic的后验概率是:
p(Z|α)=∏mM∫p(zm|θm)p(θm|α)dθm=∏mM∫∏nNp(θm,n)nznDir(θm|α)dθm=∏mM∫∏nNp(θm,n)nzn1△(α)∏nNp(θm,n)α−1dθm=∏mM1△(α)∫∏nNp(θm,n)nn+α−1dθm=∏mM△(nm+α)△(α)
注意:n_m是向量表示,代表伪计数;
同理,可以获得word-topic 的分布的后验概率是
Dir(ϕk|nk+β)
,
然后计算联合概率:
由于W是观测变量,因此我们可以获得隐变量Z的条件概率;
(注:这里可以使用变分EM模型解耦,然后估计隐变量Z的分布;另一种是使用gibbs 采样进行估计);
gibbs 采样需要已知条件概率,所以我们继续推导如下:
参考文献:
http://blog.csdn.net/baimafujinji/article/details/53946367
http://blog.csdn.net/pipisorry/article/details/51525308
http://www.cnblogs.com/pinard/p/6873703.html
LDA数学八卦








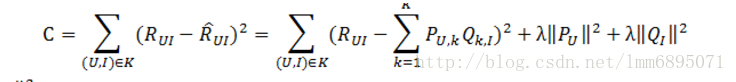




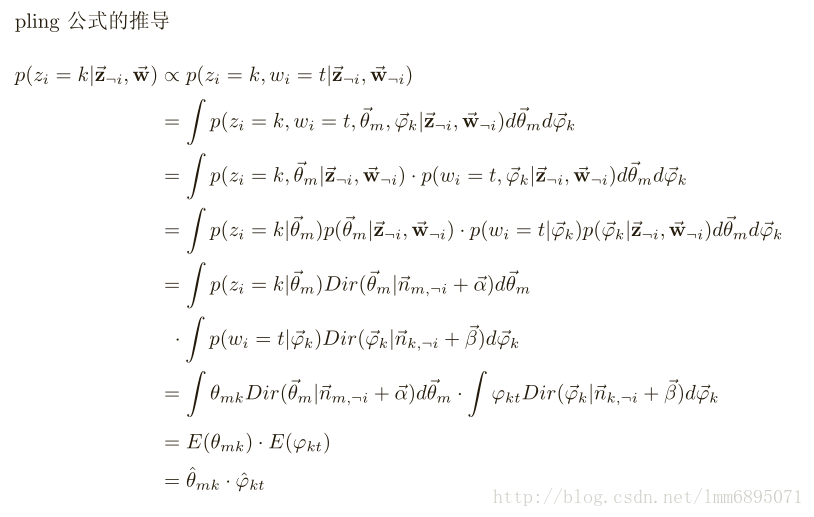
















 4402
4402

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








