TED有这样一个演讲How to learn from mistakes,演讲者主要分享了一些学习的体会,其中最主要的就是如何从自己犯过的错误中学习。我们自己学习工作中应该很有体会,踩过的坑下次就知道了。相反如果学习过程中一点错误都没用,那就需要担心自己的学习效率了。
好了,这里不是鸡汤文,还是谈谈正题吧。
梯度消失
我们同样希望自己搭建出来的神经网络能够从它的错误中学得最快,当然它们的错误由损失函数来定义。实际应用中,它是不是乖乖地学得快呢?来看一个小例子。

我们之引入三个神经元,一个输入,一个隐藏,一个输出(图上只画了隐藏神经元)。我们现在输入1,算法将学习合适的w,b使得输出为0。我们现在给w,b初始化不同的值,观察算法的学习效率。首先我们初始化w=0.6,b=0.9(注意此时的w不再是矩阵形式了)。
损失函数我们采用差平方,学习率为0.15。
下面给出该例子用tensorflow实现的源码
import tensorflow as tf
xs = tf.placeholder(tf.float32)
ys = tf.placeholder(tf.float32)
w = tf.Variable(tf.constant(0.6))
b = tf.Variable(tf.constant(0.9))
y = tf.nn.sigmoid(w*xs+b)
loss = tf.pow(ys-y, 2)/2
train_step = tf.train.GradientDescentOptimizer(0.15).minimize(loss)
sess = tf.Session()
# important step
sess.run(tf.initialize_all_variables())
for i in range(300):
_,y_o = sess.run([train_step,y], feed_dict={xs: 1, ys: 0})
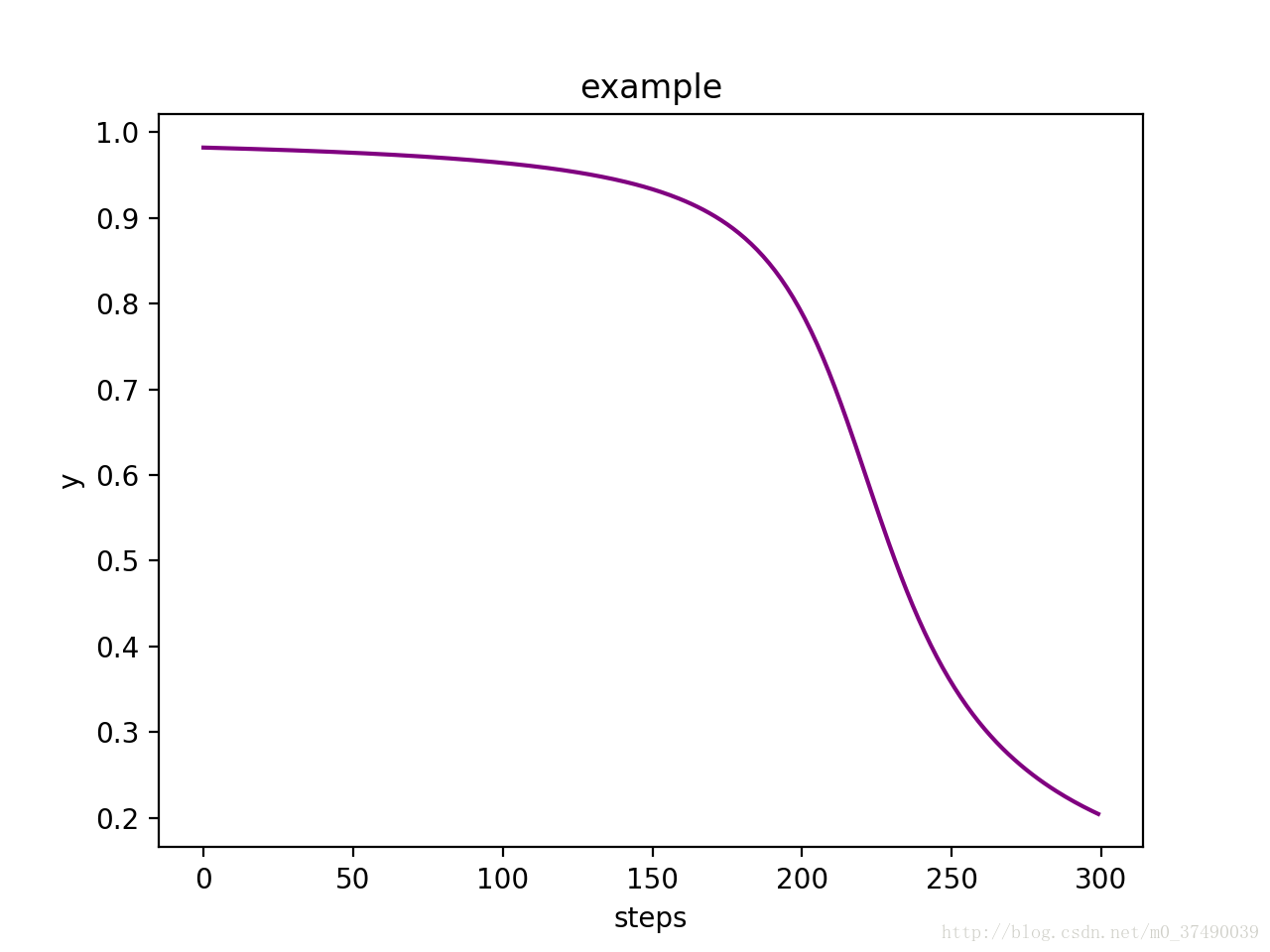
print(y_o)现在以训练的次数为横坐标,输出y为纵坐标。曲线的平滑程度可以反映出学习的效率。
图1
再来看个例子,现在我们把w和b都初始化为2,看看效果如何
图2
对比两张图可以看出,图一的算法学的很快,迅速把自己的输出逼近于0,最终的y大约在0.1。而图二呢?学得很慢,在150steps之前基本没怎么动,而最终的y大约在0.2。
越大的y意味着损失函数的值越大,所以如果用损失函数的值作为纵坐标的话得到的曲线的平滑程度和y是一致的。
越大的损失函数值也就意味着模型“犯的错“越大,仔细观察图2,发现算法在“犯错“很大的时候学得却很慢,这个和我们人是相反的,我们在犯了很大错误的时候通常都能接受教训学得很快。我们能不能找到这个问题的根本原因,从而避免这种情况的出现呢?
我们都知道,梯度下降法就是让参数沿着自己的梯度方向走,那算法学的慢是不是意味着参数的偏导值不够大呢(当然还受到learning rate的影响),那么我们就来看看这个例子中参数的偏导。首先定义损失函数,y表示真实的输出,也就是上例中的0(注意这里的y定义与刚刚不同),a表示我们模型的输出
x
x
表示输入,表示隐藏神经元的输入,则有
z=wx+b
z
=
w
x
+
b
通过激活函数后则有
a=σ(z)
a
=
σ
(
z
)
,不难求得
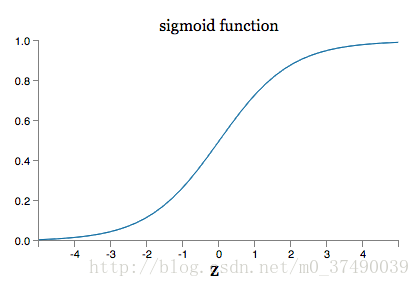
可以推断出 ∂C/∂w ∂ C / ∂ w 与 ∂C/∂b ∂ C / ∂ b 的大小取决于 σ′(z) σ ′ ( z ) ,下面是损失函数 σ σ 的图像
上图可以看出当
z>1
z
>
1
或者
z<−1
z
<
−
1
的时候,函数曲线趋于平滑,其导数值也就趋向于0。
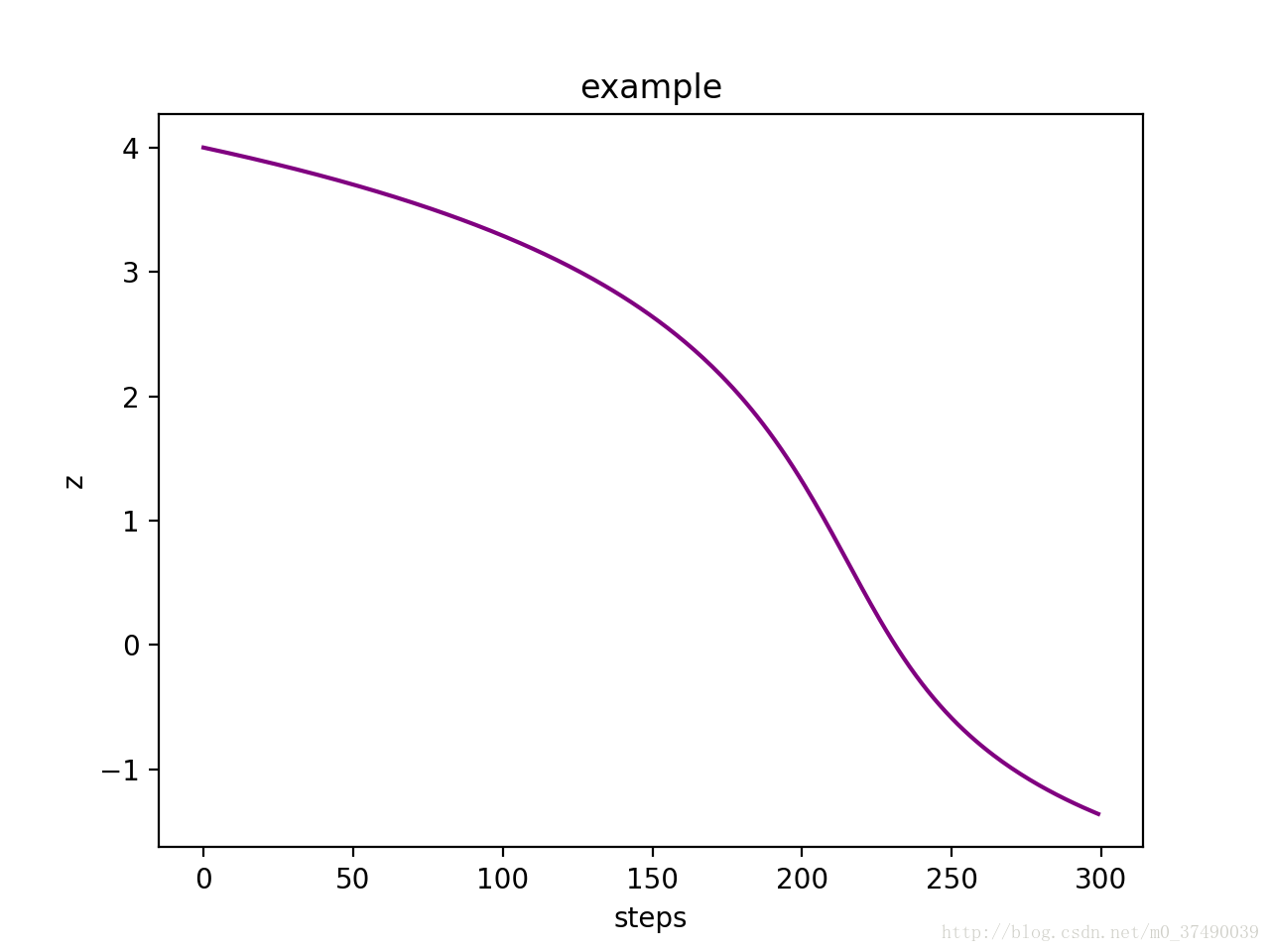
我们再来看看上面例子2中
z
z
的变化曲线
可以看出在step150之前,的值都是大于2的,也意味着在这之前的 σ′(z) σ ′ ( z ) 的值都是很小很小的,这才导致了我们算法学得很慢。
到此,我们找出了例2相比于例1训练速度慢的真正原因了:如果权重初始化得太大,激活后的值基本在sigmoid两侧,而这两侧的梯度几乎为0。那是不是选择小的初始化权值就可以避免这个问题呢?上述例子看上去是这样的。(如何合理初始化权值可以参阅深度神经网络调参之权值初始化)事实上我们的神经网络会有很多个神经元组成,这样的神经元分布在不同的网络层上,很容易出现一些神经元的值跑到sigmoid两侧去,这样经过几层传播,就带来了梯度消失。如何解决这个问题呢?当然,可以换成其他激活函数,如:ReLu等,事实上sigmoid在实际应用中并不是一个很好的激活函数。还有一个办法就是引入其他损失函数。
交叉熵损失函数
交叉熵损失函数通用的定义如下
ai a i 是模型的输出,表示当前输入被分为第i类的概率
yi y i 是当前的输入对应的label(是第i类为1,否则为0)
考虑二分类的情况
简单地理解交叉熵损失函数刻画了 a a (预测分布)与(实际分布)之间的距离,两者分布相差越大,距离就越大(函数值越大),两者分布越接近,距离就越小(函数值越小)。所以我们只需要不断缩小交叉熵损失函数值就能使得预测越来越接近实际。
下面来看看这样一个损失函数有什么好处呢?
我们把它应用于上面的例子
不难求得
发现少了 σ′(z) σ ′ ( z ) ,上一节我们发现了训练缓慢的原因就是应该它的存在,现在少了它训练理应就能快很多。
感兴趣的话可以试下,修改上面代码中的损失函数为
loss = -tf.reduce_mean(ys*tf.log(y))注意ys此时不能为0了,否则loss恒为0
因此,我们在用sigmoid作为激活函数时,通常都是用交叉熵损失函数的。原因就是我们在随机初始化参数后,一旦一个输出层的神经处于饱和状态,使用差平方作损失的话,训练学习就变得十分缓慢。
应用于多层多分类神经网络的交叉损失熵函数的推导可参考简单易懂的softmax交叉熵损失函数求导
值得注意的是,交叉熵损失函数只是在求输出层上的参数不需要乘上激活函数的导数,其他层仍然需要乘上激活函数的导数,因此,采用交叉熵损失函数只能缓解梯度消失问题,不能完全避免。























 5803
5803

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








