常见的损失函数(loss function)总结及其与准确率等评估指标之间的关系

损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样。

损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。

• 0-1损失函数
  0-1损失是指预测值和目标值不相等为1， 否则为0:
  
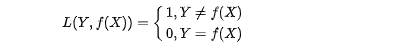
  特点：
  (1)0-1损失函数直接对应分类判断错误的个数，但是它是一个非凸函数，不太适用。该损失函数能直观地刻画分类的错误率，但分类太过严格，如果真实值为 1，预测值为 0.999，显然该分类应该是一个正确的分类，但上述定义则会判定为预测错误。而且该函数是一个非凸、非光滑的函数，使得算法很难直接对该函数进行优化。因此 0-1 损失函数很少被应用到。
  (2)感知机就是用的这种损失函数。但是相等这个条件太过严格，因此可以放宽条件，即满足 |Y-f(x)|<T时认为相等，
  

• 绝对值函数
  绝对值损失函数是计算预测值与目标值的差的绝对值：(除以样本个数就是我们平常所说的L1 loss)
  

• log对数损失函数
  log对数损失函数的标准形式如下：
  
  
  这个损失函数就比较难理解了。事实上，该损失函数用到了极大似然估计的思想。P(Y|X)通俗的解释就是：在当前模型的基础上，对于样本X，其预测值为Y，也就是预测正确的概率。由于概率之间的同时满足需要使用乘法，为了将其转化为加法，我们将其取对数。最后由于是损失函数，所以预测正确的概率越高，其损失值应该是越小，因此再加个负号取个反。
  特点：
  (1) log对数损失函数能非常好的表征概率分布，在很多场景尤其是多分类，如果需要知道结果属于每个类别的置信度，那它非常适合。
  (2)健壮性不强，相比于hinge loss对噪声更敏感。
  (3)逻辑回归的损失函数就是log对数损失函数。

• 平方损失函数
  平方损失函数标准形式如下：(除以样本个数就是我们平常所说的L2 loss)
  
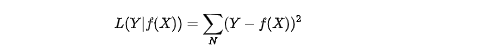
  特点：
  (1)经常应用于回归问题

• 指数损失函数
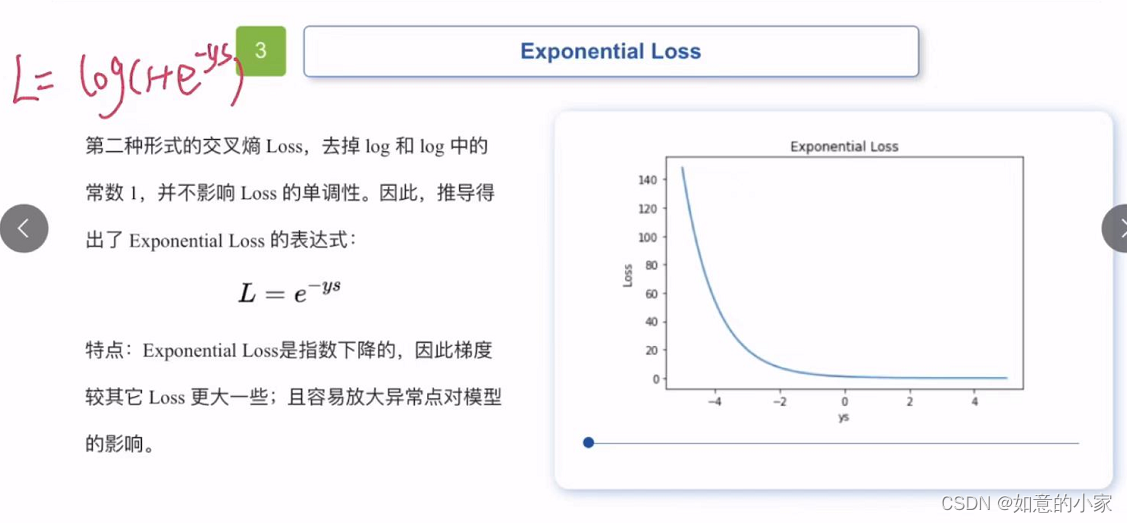
  指数损失函数的标准形式如下：
  
  
  特点：
  (1)对离群点、噪声非常敏感。经常用在AdaBoost算法中。

• Hinge 损失函数
  Hinge损失函数标准形式如下：
  
  
  ys>1,Loss=0，预测完全正确
  ys<0,1-ys>1,Loss>1，预测完全错误
  0<ys<1,0<Loss<1，虽然预测正确但是有损失
  特点：
  (1)hinge损失函数表示如果被分类正确，损失为0，否则损失就为1-yf(x)。SVM就是使用这个损失函数。
  (2)一般的 f(x)是预测值，在-1到1之间， y是目标值(-1或1)。其含义是， f(x)的值在-1和+1之间就可以了，并不鼓励|f(x)|>1，即并不鼓励分类器过度自信，让某个正确分类的样本距离分割线超过1并不会有任何奖励，从而使分类器可以更专注于整体的误差。
  (3) 健壮性相对较高，对异常点、噪声不敏感，但它没太好的概率解释。

• 感知损失函数
  感知损失函数的标准形式如下：
  
  特点：
  (1)是Hinge损失函数的一个变种，Hinge loss对判定边界附近的点(正确端)惩罚力度很高。而perceptron loss只要样本的判定类别正确的话，它就满意，不管其判定边界的距离。它比Hinge loss简单，因为不是max-margin boundary，所以模型的泛化能力没 hinge loss强。

• 交叉熵损失函数 (Cross-entropy loss function)
  交叉熵损失函数的标准形式如下:
  
  注意公式中x表示样本， y表示实际的标签， α表示预测的输出，n表示样本总数量。
  特点：
  (1)本质上也是一种对数似然函数，可用于二分类和多分类任务中。
  二分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）：
  
  多分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）：
  
  (2)当使用sigmoid作为激活函数的时候，常用交叉熵损失函数而不用均方误差损失函数，因为它可以完美解决平方损失函数权重更新过慢的问题，具有“误差大的时候，权重更新快；误差小的时候，权重更新慢”的良好性质。
  
  损失函数与准确率等关系：
  loss 是我们预先设定的损失函数计算得到的损失值；accuracy 是模型在数据集上基于给定 label 得到的评估结果。Loss一般是在0到某上界(包括正无穷)之间的量，acc是在0到1之间，而且给定样本量后一般是离散的。之间没有特别简单的可以写下来的关系。简单来说：

• 通过模型在 dev/test 集上的 accuracy ，计算模型正确分类的样本数与总样本数之比以衡量模型的效果，目标是对模型的效果进行度量

• 通过损失函数的计算，从而更新我们的模型参数，目标是为了减小优化误差(Optimization error)，即在损失函数与优化算法的共同作用下，减小模型的经验风险。

 想了一个很不恰当的例子：loss 是父母给我们报了一堆辅导班，辅以棍棒或是糖果优化算法，诱导我们通过辅导班增强自己的能力，
 减少我们的能力值与辅导班声称的能力值之间的差距。accuracy 则是我们的高考成绩。

相关链接：
https://blog.csdn.net/u014421797/article/details/104689384
https://www.zhihu.com/question/264892967
https://zhuanlan.zhihu.com/p/58883095