不相交集合求并的路径压缩

【0】README

0.1）本文总结于 数据结构与算法分析， 源代码均为原创， 旨在实现 对不相交集合的路径压缩操作；
0.2）对求并后的集合进行路径压缩，目的是降低集合（合并树）的深度，减少find 操作的时间复杂度；
0.3） for introduction to non-intersect set ADT ,please refet to http://blog.csdn.net/PacosonSWJTU/article/details/49716905 , and for details of finding or unionSet operations towards non-intersect set , please refer to http://blog.csdn.net/pacosonswjtu/article/details/49717009

---

【1】 路径压缩相关

1.1）基于这样的观察：执行 Union操作 的任何算法都将产生相同的最坏情形的树，因为它必然会随意打破树间的平衡。因此，无需对整个数据结构重新加工而使算法加速的唯一方法是： 对Find 操作做些更聪明的工作；
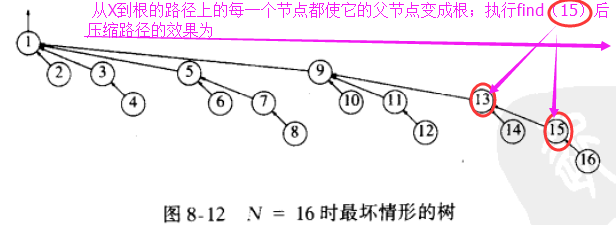
1.2）路径压缩定义：设操作是Find（X）， 此时路径压缩的效果是， 从X到根的路径上的每一个节点都使它的父节点变成根；执行find（15）后压缩路径的效果为：

对路径压缩算法的分析（Analysis）

• A1）路径压缩的实施在于 使用额外的两次指针移动， 节点13和14 现在离根近了一个位置， 而节点15和16离根近了两个位置；
• A2）因此， 对这些节点未来的快速访问将由于花费 额外的工作来进行路径压缩而得到补偿；

1.3）路径压缩对 基本的 Find操作改变不大。对 Find 操作来说，唯一的变化是 使得 S[X] 等于 由Find 返回的值；这样，在集合的根被递归地找到以后， X 就直接指向了它， 对通向根的路径上的每一个节点这将递归地出现，因此实现了路径压缩；
1.4）路径压缩可以和 大小求并完全兼容，这就使得两个例程可以同时实现；
1.5）路径压缩不完全与 按高度求并兼容，因为路径压缩可以改变树的高度；

---

【2】source code + printing results

2.1）download source code：
https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter8/p206_pathCompression.c

• souce code statements：路径压缩源代码中使用的集合求并方法是： 按大小求并：

2.2）source code at a glance：

#include <stdio.h>
#include <malloc.h>

#define ElementType int
#define Error(str) printf("\n error: %s \n",str) 

struct UnionSet;
typedef struct UnionSet* UnionSet;

// we adopt the child-sibling expr
struct UnionSet
{
    int parent;
    int size;
    ElementType value;
};

UnionSet makeEmpty(); 
UnionSet* initUnionSet(int size, ElementType* data);
void printSet(UnionSet* set, int size);
void printArray(ElementType data[], int size);
int find(int index, UnionSet* set);
void pathCompress(int, UnionSet*);

// initialize the union set 
UnionSet* initUnionSet(int size, ElementType* data)
{
    UnionSet* set;  
    int i;

    set = (UnionSet*)malloc(size * sizeof(UnionSet));
    if(!set)
    {
        Error("out of space, from func initUnionSet");        
        return NULL;
    }   

    for(i=0; i<size; i++)
    {
        set[i] = makeEmpty();
        if(!set[i])
            return NULL;
        set[i]->value = data[i];
    }

    return set;
}

// allocate the memory for the single UnionSet and evaluate the parent and size -1
UnionSet makeEmpty()
{
    UnionSet temp;

    temp = (UnionSet)malloc(sizeof(struct UnionSet));
    if(!temp)
    {
        Error("out of space, from func makeEmpty!");        
        return NULL;
    }

    temp->parent = -1;
    temp->size = 1;
    return temp;
}


// merge set1 and set2 by size
void setUnion(UnionSet* set, int index1, int index2)
{
    //judge whether the index1 or index2 equals to -1 ,also -1 represents the root
    if(index1 != -1)
        index1 = find(index1, set);
    if(index2 != -1)
        index2 = find(index2, set);

    if(set[index1]->size > set[index2]->size)
    {
        set[index2]->parent = index1;
        set[index1]->size += set[index2]->size;
    }
    else
    {
        set[index1]->parent = index2;
        set[index2]->size += set[index1]->size;
    }
} 

//find the root of one set whose value equals to given value
int find(int index, UnionSet* set) 
{
    UnionSet temp;  

    while(1)
    {
        temp = set[index];
        if(temp->parent == -1)
            break;
        index = temp->parent;
    }

    return index;       
}   

// conducting path compression towards union set with given index
void pathCompress(int index, UnionSet* set)
{   
    int root;
    int i;
    int parent;

    //1st step: find the top root contains the element under index  
    root = find(index, set);

    //2nd step: path compression begins
    i = set[index]->parent;
    set[index]->parent = root;
    while(i != -1) 
    {       
        parent = set[i]->parent;                
        if(parent == root)
            break;
        set[i]->parent = root;
        i = parent;
    }
}

int main()
{
    int size;
    UnionSet* unionSet;
    ElementType data[] = {110, 245, 895, 658, 321, 852, 147, 458, 469, 159, 347, 28};

    size = 12;
    printf("\n\t====== test for conducting path compression towards union set by size ======\n");
    //printf("\n\t=== the initial array is as follows ===\n");
    //printArray(data, depth); 

    printf("\n\t=== the init union set are as follows ===\n");
    unionSet = initUnionSet(size, data); // initialize the union set over
    //printSet(unionSet, size);

    printf("\n\t=== after union(0, 1) + union(2, 3) + union(4, 5) + union(6, 7) + union(8, 9) + union(10 ,11) ===\n");
    setUnion(unionSet, 0, 1);
    setUnion(unionSet, 2, 3);
    setUnion(unionSet, 4, 5);
    setUnion(unionSet, 6, 7);
    setUnion(unionSet, 8, 9);   
    setUnion(unionSet, 10, 11); 
    //printSet(unionSet, size);

    printf("\n\t=== after union(1, 3) + union(5, 7) + union(9, 11) ===\n");
    setUnion(unionSet, 1, 3);
    setUnion(unionSet, 5, 7);
    setUnion(unionSet, 9, 11);
    //printSet(unionSet, size);  

    printf("\n\t=== after union(3, 7) + union(7, 11) ===\n");
    setUnion(unionSet, 3, 7);
    setUnion(unionSet, 7, 11);  
    printSet(unionSet, size); 

    printf("\n\t=== after pathCompress(0, unionSet) + pathCompress(8, unionSet) ===\n");
    pathCompress(0, unionSet) ;
    pathCompress(8, unionSet);
    printSet(unionSet, size); 

    return 0;
}

void printArray(ElementType data[], int size)
{
    int i;

    for(i = 0; i < size; i++)    
        printf("\n\t data[%d] = %d", i, data[i]);                    
    printf("\n\n");
} 

void printSet(UnionSet* set, int size)
{
    int i;
    UnionSet temp;

    for(i = 0; i < size; i++)
    {       
        temp = set[i];
        printf("\n\t parent[%d] = %d", i, temp->parent);                
    }
    printf("\n");
}

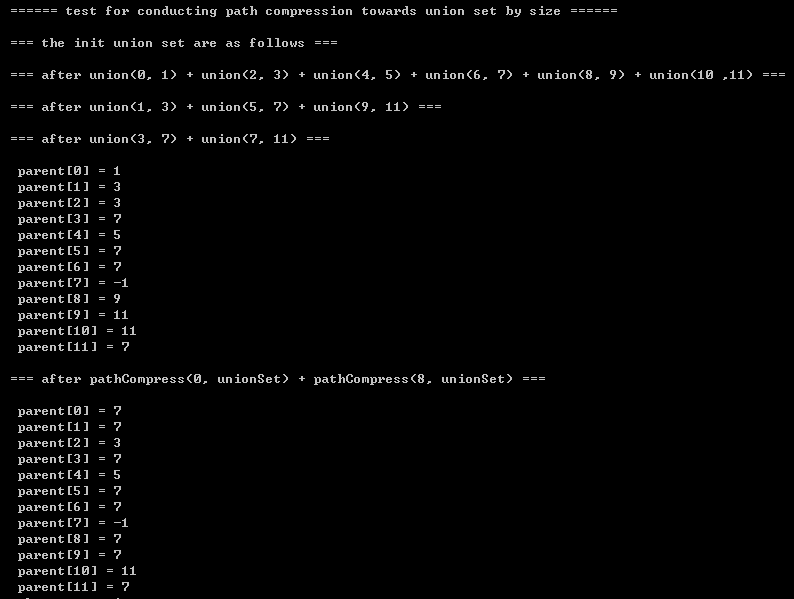
2.3）printing results：