LBP(local binary pattern)是一种用来描述图像局部纹理特征的算子。原始的LBP于1994年提出,它反映内容是每个像素与周围像素的关系。后被不断的改进和优化,分别提出了LBP旋转不变模式、LBP均匀模式等。
一:原始的LBP
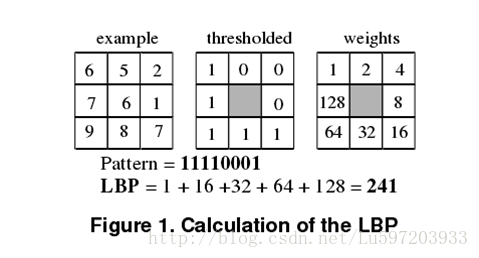
给出一个简单的案例计算LBP:如下图,周围8个像素点比中间点像素值大(或者相等)的记为1,小的记为0,这样就得到二值图,然后按顺时针方向得到二进制串10001111
这样中间点的像素值就用241来代替。注意这里的计算LBP的顺序并没有硬性要求,只是一个量化公式,在同一处理中保持相同的顺序即可。
下面给出LBP的计算公式:
二、旋转不变的LBP模式<LBPROT>
原始的LBP不具有旋转不变性,这样我们就提出了旋转不变的LBP模式。旋转不变的LBP计算公式如下:
这样计算出来的LBP共有36种,分布情况如下面两幅图:
其中白点代表1,黑点代表0。
三:均匀LBP模式
旋转LBP模式同样存在缺陷,大量的实验证明LBP模式的36种情况在一幅图像中分布出现的频率差异较大,得到的效果并不是很好。因此人们提出了均匀LBP模式即uniform LBP。
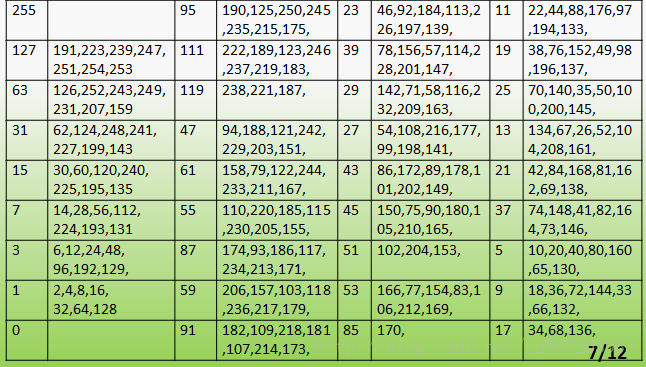
均匀模式就是一个二进制序列从0到1或是从1到0的变过不超过2次(这个二进制序列首尾相连)。比如:10100000的变化次数为3次所以不是一个uniform pattern。所有的8位二进制数中共有58(变化次数为0的有2种,变化次数为1的有0种,变化次数为2的有56种)个uniform pattern.为什么要提出这么个uniform LBP呢,因为研究者发现他们计算出来的大部分值都在这58种之中,可达到90%以上,所以他们把值分为59类,58个uniform pattern为一类,其它的所有值为第59类。59=(2+0+56)+1,这样直方图从原来的256维变成59维。起到了降维的作用。
计算公式:
应用:
在模式识别如判断两幅图片的相似性时,我们可以统计这两幅图像的LBP特征的直方图。这样,在原始的LBP模式中,统计的直方图可以当做一个256维的向量。直接这样判断,很多时候会因为“位置没有对准”而产生很大的误差。大量研究表明,此时我们可以将一幅图片划分为若干的子区域,对每个子区域内的每个像素点都提取LBP特征,然后,在每个子区域内建立LBP特征的统计直方图。如此一来,每个子区域,就可以用一个统计直方图来进行描述;整个图片就由若干个统计直方图组成。比如将一幅图像划分为10*10个区域,这样得到向量的维数就是256*10*10。而针对uniform LBP,此时向量的维数就是59*10*10, 从而达到降维的目的。
目前,LBP局部纹理提取算子,已经成功应用在指纹识别、字符识别、人脸识别、车牌识别等领域。
Code:
原始的LBP:
- void LBP(Mat &image, Mat &result)
- {
- for(int y = 1; y < image.rows-1; y ++)
- {
- for(int x = 1; x < image.cols-1; x++)
- {
- uchar neighbor[8] = {0};
- neighbor[0] = image.at<uchar>(y-1, x-1);
- neighbor[1] = image.at<uchar>(y-1, x);
- neighbor[2] = image.at<uchar>(y-1, x+1);
- neighbor[3] = image.at<uchar>(y, x+1);
- neighbor[4] = image.at<uchar>(y+1, x+1);
- neighbor[5] = image.at<uchar>(y+1, x);
- neighbor[6] = image.at<uchar>(y+1, x-1);
- neighbor[7] = image.at<uchar>(y, x-1);
- uchar center = image.at<uchar>(y, x);
- uchar temp = 0;
- for(int k = 0; k < 8; k++)
- {
- temp += (neighbor[k] >= center)* (1<<k); // 计算LBP的值
- }
- result.at<uchar>(y,x) = temp;
- }
- }
- }
- int main()
- {
- Mat image = imread("F:\\lena.png", 0);
- if(!image.data)
- {
- cout << "Fail to load image" << endl;
- return 0;
- }
- Mat result;
- result.create(Size(image.cols, image.rows), image.type());
- LBP(image, result);
- namedWindow("result", 0);
- imshow("result", result);
- waitKey(0);
- return 0;
- }
- // 计算跳变次数
- int getHopCount(int i)
- {
- int a[8] = {0};
- int cnt = 0;
- int k = 7;
- while(i)
- {
- a[k] = i&1;
- i = i >> 1;
- --k;
- }
- for(k = 0; k < 7; k++)
- {
- if(a[k] != a[k+1])
- {
- ++cnt;
- }
- }
- if(a[0] != a[7])
- {
- ++cnt;
- }
- return cnt;
- }
- // 降维数组 由256->59
- void lbp59table(uchar *table)
- {
- memset(table, 0, 256);
- uchar temp = 1;
- for(int i = 0; i < 256; i++)
- {
- if(getHopCount(i) <= 2) // 跳变次数<=2 的为非0值
- {
- table[i] = temp;
- temp ++;
- }
- }
- }
- void uniformLBP(Mat &image, Mat &result, uchar *table)
- {
- for(int y = 1; y < image.rows-1; y ++)
- {
- for(int x = 1; x < image.cols-1; x++)
- {
- uchar neighbor[8] = {0};
- neighbor[0] = image.at<uchar>(y-1, x-1);
- neighbor[1] = image.at<uchar>(y-1, x);
- neighbor[2] = image.at<uchar>(y-1, x+1);
- neighbor[3] = image.at<uchar>(y, x+1);
- neighbor[4] = image.at<uchar>(y+1, x+1);
- neighbor[5] = image.at<uchar>(y+1, x);
- neighbor[6] = image.at<uchar>(y+1, x-1);
- neighbor[7] = image.at<uchar>(y, x-1);
- uchar center = image.at<uchar>(y, x);
- uchar temp = 0;
- for(int k = 0; k < 8; k++)
- {
- temp += (neighbor[k] >= center)* (1<<k); // 计算LBP的值
- }
- result.at<uchar>(y,x) = table[temp]; // 降为59维空间
- }
- }
- }
- int main()
- {
- uchar table[256];
- lbp59table(table);
- Mat image = imread("F:\\lena.png", 0);
- if(!image.data)
- {
- cout << "Fail to load image" << endl;
- return 0;
- }
- Mat result;
- result.create(Size(image.cols, image.rows), image.type());
- uniformLBP(image, result, table);
- namedWindow("uniformResult", 0);
- imshow("uniformResult", result);
- waitKey(0);
- return 0;
- }
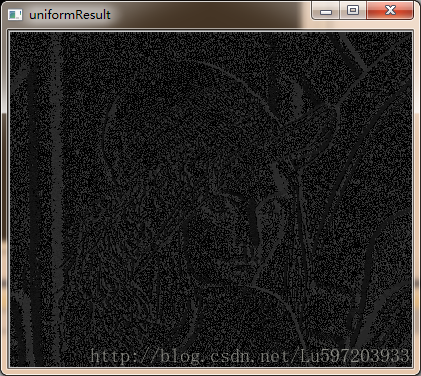
Result:
原图:
原始LBP:
uniform LBP:
参考文献:文章:Multiresolution Gray-Scale and Rotation Invariant Texture Classificationwith Local Binary Patterns
作者:小村长 出处:http://blog.csdn.net/lu597203933 欢迎转载或分享,但请务必声明文章出处。 (新浪微博:小村长zack, 欢迎交流!)
- 上一篇:Opencv2系列学习











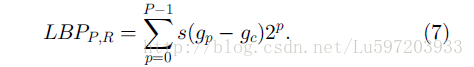
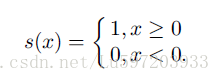


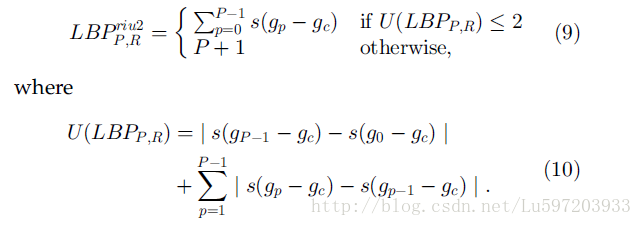
















 1607
1607

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








