主成分分析与隐变量模型

$\,\,\,\,\,\,\,\,$用于聚类的无监督方法——将数据对象分割成有限数目的不相关组，使得同组中的数据对象具有某些相似性。现在引入第二类无监督方法，这种方法通常被归类于投影技术
$\,\,\,\,\,\,\,\,$用于处理高维的数据集，以及如何通过将数据集投影到低维空间对数据进行可视化或者特征选择。这些技术用于处理更大规模的隐变量模型

---

---

参数的数量随着维度M的增加而增加，我们将M维数据投影到D维的同时，希望在某种程度上保留感兴趣的属性

---

---

方差——感兴结构的代表
对数据进行投影操作时，我们希望尽可能保留数据中感兴趣的结构
数据在每个一维空间的方差可以通过下式计算：
$\sigma^2=\frac{1}{N}\sum_{n=1}^N (x_{n}-\mu_{x})^2$
如果想要表达数据的聚类结构，在使方差最大的方向上对数据进行投影更能保留这一结构特征
基于这个原因，当考虑投影方向时，方差是一个很好的最大化度量标准。因此在大多流行的投影技术中，如主成分分析，使用方差作为最大化度量的标准。

---

---

主成分分析

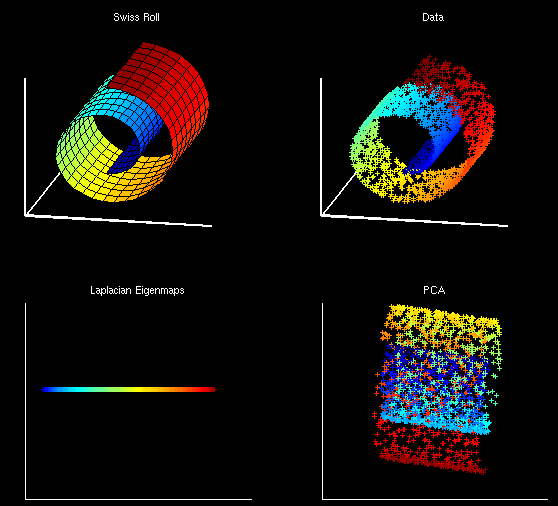
主成分分析（PCA）可能是目前应用最为广泛的一种统计技术，用于将高维数据投影到低维空间。在机器学习中，该技术大多应用于数据可视化和特征选择。PCA定义了一组线性投影：每个投影维度都是原始数据维度的一个线性组合

---

---

为了简化模型，我们构造 $\bar{y}=\frac1N\sum_{n=1}^Ny_{n}=0$

从投影D=1维开始。
$x_{n}=w^Ty_{n}$
$\sigma_{x}^2=\frac1N\sum_{n=1}^N(x_{n}-\bar{x})^2$

得到：
$\sigma_{x}^2=w^TCw$
C是样本协方差矩阵，定义为
$C=\frac1N\sum_{n=1}^N(y_{n}-\bar{y})(y_{n}-\bar{y})^T$

---

---

结合条件 $w^Tw=1$,利用拉格朗日方法
最大化： L=wTCw−λ(w