感知机模型、学习算法、收敛性证明

1、感知机

学习资料：《统计学习方法》，cs229讲义，其他。

感知机是用来进行二类分类的分类模型，而感知机的学习过程就是求出将训练数据进行线性划分的分离超平面过程。下面会给出感知机模型，接着进行学习，最后证明算法的收敛性。

1.1、感知机模型

看下面的图，有两类点，记为-1和+1(负累和正类)，我们需要求一条直线（超平面，用$wx+b=0$来表示）来将它们进行划分。我们最后需要得到参数$w$和$b$，参数求解的过程就是感知机学习过程了。

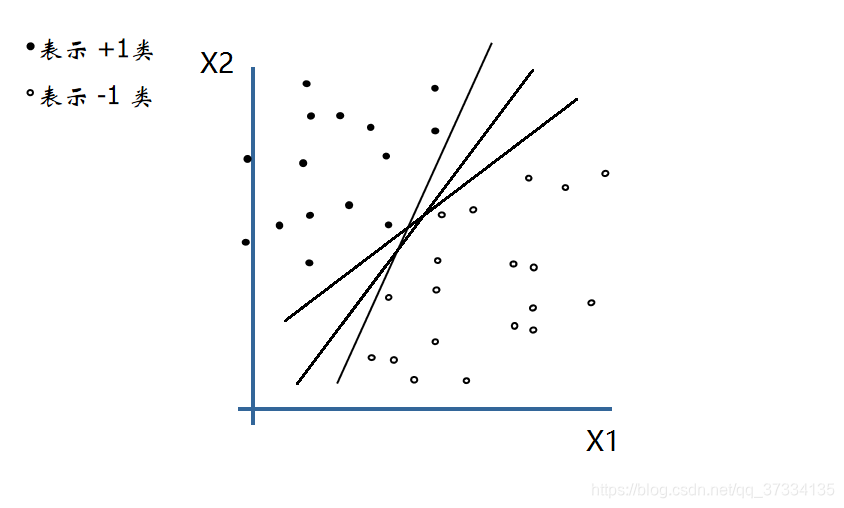
假设输入空间$X$是m维向量，输出空间 Y = { + 1 , − 1 } Y=\{+1,-1\} Y={+1,−1}。输入 x = { x 1 , x 2 , . . . , x m } x=\{x^1,x^2,...,x^m\} x={x1,x2,...,xm}表示实例的特征向量；输出$y$表示实例的类别。那么感知机模型表示如下：

$f(x)=sign(wx+b)$

其中$w$称为权值，$b$称为偏置，$wx=w^1{x}^1+w^2{x}^2+...+w^m{x}^m$，当$wx+b>0$时候$sign(wx+b)=+1$,当$wx+b<0$ 时候 $sign(wx+b)=-1$。

现在要做的是求出这样的超平面$wx+b=0$将空间分成正类和负类，接下来进行模型的学习，求解参数$w$和$b$。

1.2、感知机的学习算法

先给出数据集线性可分的定义：

给定一个数据集 T = { ( x 1 , y 1 ) , . . . , ( x n , y n ) } T=\{(x_1,y_1),...,(x_n,y_n)\} T={(x1​,y1​),...,(xn​,yn​)}，其中$x_i$ 是m维向量（m个特征）, y i = { + 1 , − 1 } y_i=\{+1,-1\} yi​={+1,−1}表示类别，如果存在某个超平面$S$
$wx+b=0$
能够将训练集的正实例点和负实例点正确的划分到超平面两侧，即：对于$y=+1$的实例有$w{x}_i+b>0$，对于$y=-1$的实例有$w{x}_i+b<0$，写到一起也就是$y_i(w{x}_i+b)>0$那么就说数据集$T$是线性可分的。

如果给定数据集是线性可分的，那么我们就可以去求这样的超平面 $wx+b=0$，参数$w,b$求解过程也就成了感知机学习过程。我们定义损失函数，通过最小化损失函数值来进行参数的求解。

定义一个点$x_i$到超平面$wx+b=0$的距离：

$\frac{1}{||w||}|w{x}_i+b|$

其中$||w||$是向量$w$的$L_2$范数，举个例子来说，假设超平面表示为$x_1+2x_2+3=0$那么点(1,-2)刚好在上面，而 $(1,1)$带入$x_1+x_2+3$中结果是6，而权重和偏置变成了原来两倍那么$(1,1)$的距离就成了原来的2倍，所以我们使用了距离除以$L_2$范数进行距离的固定化，这样权重和偏置就算成倍增加那么距离也不会变了。这里叫做集合间隔，而不进行标准化的叫做函数间隔。

对于误分类的数据$(x_i,y_i)$，满足$y_i(w{x}_i+b)<0=>-y_i(w{x}_i+b)>0$ ，所以该误分类的点到超平面的距离为:

$-\frac{1}{||w||}{y}_i(w{x}_i+b)$

$\frac{1}{||w||}$可以直接去掉，只要响应的变化内部系数即可，所以所有误分类的点$x_i\in M$到超平面的距离之和为：

$J(w,b)=-\sum _{x_i\in M}{y}_i(w{x}_i+b)$

这就是我们的损失函数（也称做感知机学习的经验风险函数），我们的学习要求使得这个损失函数值最小，显然损失函数的值是大于等于0，只有当超平面将数据集正确划分了，那么就是没有误分类点此时损失函数值就是0。

超平面是连续可导的，所以损失函数也是连续可导，这里要求最小值，所以可以使用梯度下降（比如随机梯度下降）

$w_j:=w_j-\alpha \frac{\partial J(w,b)}{\partial w_j}$ for every j（表示第j个特征）
$b:=b-\alpha \frac{\partial J(w,b)}{\partial b}$

将损失函数带入求导可得：

$w_j:=w_j+\alpha \sum _{x_i\in M}{y}_i{x}_i^j$
$b:=b+\alpha \sum _{x_i\in M}{y}_i$
由于是使用随机梯度下降，那么伪代码我们写成下面的形式

f o r i = i 1 − &gt; i M { w j : = w j + α y i x i j ( 针 对 没 个 j 同 时 进 行 ) ， b : = b + α y i } for i = i_1 -&gt; i_M \{w_j:= w_j + \alpha y_i x_i^j(针对没个j同时进行)，b:=b+\alpha y_i\} fori=i1​−>iM​{wj​:=wj​+αyi​xij​(针对没个j同时进行)，b:=b+αyi​}

具体的算法如下：

1. 选取初始值 $w_0,b_0$
2. 训练集中选取数据$(x_i,y_i)$
3. 找误分类点,即$y_i(w{x}_i+b)<=0$，那么进行上面的$w$和$b$的更新操作，转到步骤2。直到没有误分类点为止。

1.3、算法的收敛性

对于上面的算法会不会存在，一直找不到这样的超平面导致会一直循环下去呢？答案是不会，也就是说经过有限次迭代可以得到一个将训练集正确划分的超平面，也就是说该算法具有收敛性。

为方便起见，进行如下的转换:
$\overline{w}=(w^T,b)$,$\overline{x}=(x^T,1{)}^T$，为了方便起见后面将$T$给去掉了。
那么$w\cdot x+b=0$就可以表示成$\overline{w}\cdot \overline{x}=0$

下面来进行证明收敛性

给定训练集 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } \{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\} {(x1​,y1​),(x2​,y2​),...,(xn​,yn​)}是线性可分的。

（1）、证明存在满足条件$||{\overline{w}}_e||=1$的超平面 ${\overline{w}}_e\cdot \overline{x}=w_e\cdot x+b_e=0$，将训练集正确分开，且存在$\gamma >0$，对所有的 $i=1,2,\dots ,n$都有

$y_i({\overline{w}}_e\cdot {\overline{x}}_i)=y_i(w_e\cdot x_i+b_e)>=\gamma$

证明： 由于训练集线性可分，自然就存在超平面 $S$将其正确划分，对于该超平面我们只需要规范一下，或者说同比例增加或者减少参数大小，是的满足$\overline{w}=1$即可，那么该平面就是我们想要的，记做 ${\overline{w}}_e\cdot \overline{x}=w_e\cdot x+b_e=0$。此时必然满足

$y_i({\overline{w}}_e\cdot {\overline{x}}_i)=y_i(w_e\cdot x_i+b_e)>0$，我们将$\gamma$ 记做 $\min y_i(w_e\cdot x_i+b_e)$，所以就得到对任意 $i=1,2,\dots ,n$, 都有 $y_i({\overline{w}}_e\cdot {\overline{x}}_i)=y_i(w_e\cdot x_i+b_e)>=\gamma$

（2）、令$R=\underset{i\in [1,n]}{\max }||{\overline{x}}_i||$ ，则前面提到的感知机算法的误分类次数$k$（或者说参数的迭代的轮次）满足如下不等式

$k<=(\frac{R}{\gamma }{)}^2$

补充：如果满足了(2)那么就说明了算法的收敛性，也就是一定的迭代次数后能得到满足要求的超平面。下面开始证明

假设初始参数${\overline{w}}_0=0$，如果实例被误分类那么需要继续更新参数。对于第$k-1$次参数${\overline{w}}_{k-1}$，对应的误分类实例为${\overline{x}}_i$，由于是误分类很自然的有$y_i({\overline{w}}_{k-1}\cdot {\overline{x}}_i)=y_i(w_{k-1}\cdot x_i+b_{k-1})<0$

根据前面写的随机梯度下降得到的公式如下（将所有的特征$j$全部写到了一起，所以没有了$w_j$）：

$w_k=w_{k-1}+\alpha y_i{x}_i$
$b_k=b_{k-1}+\alpha y_i$

$k-1$表示上一轮，$k$表示当前，两个写到一起就是

${\overline{w}}_k={\overline{w}}_{k-1}+\alpha y_i{\overline{x}}_i$

（2.1）、证明${\overline{w}}_e\cdot {\overline{w}}_k>=k\alpha \gamma$

证明：${\overline{w}}_e\cdot {\overline{w}}_k={\overline{w}}_e({\overline{w}}_{k-1}+\alpha y_i{x}_i)={\overline{w}}_e\cdot {\overline{w}}_{k-1}+\alpha y_i{\overline{w}}_e{x}_i>={\overline{w}}_e\cdot {\overline{w}}_{k-1}+\alpha \gamma >={\overline{w}}_e\cdot {\overline{w}}_{k-2}+2\alpha \gamma >=...>={\overline{w}}_e\cdot {\overline{w}}_0+k\alpha \gamma =k\alpha \gamma$

（2.2）、证明 $||{\overline{w}}_k|{|}^2<=k{\alpha }^2{R}^2$

证明：$||{\overline{w}}_k|{|}^2={\overline{w}}_k\cdot {\overline{w}}_k={\overline{w}}_{k-1}\cdot {\overline{w}}_{k-1}+2\alpha y_i{\overline{w}}_{k-1}{\overline{x}}_i+{\alpha }^2||{\overline{x}}_i|{|}^2<=||{\overline{w}}_{k-1}|{|}^2+{\alpha }^2{R}^2<=...<=k{\alpha }^2{R}^2$

根据(2.1)和(2.2)得到 $k\alpha \gamma <={\overline{w}}_e\cdot {\overline{w}}_k<=||{\overline{w}}_e||\cdot ||{\overline{w}}_k||=||{\overline{w}}_k||<=\sqrt{k}\alpha R$
$=>k^2{\alpha }^2{\gamma }^2<=k{\alpha }^2{R}^2$，最后得到 $k<=(\frac{R}{\gamma }{)}^2$