KNN算法中常用的距离计算公式

　　KNN，英文全称为K-nearst neighbor，中文名称为K近邻算法，它是由Cover和Hart在1968年提出来的。
　　KNN算法流程：
　　输入：训练数据集　　

$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$
　　其中， $x_i \in \mathcal{X} \subseteq R^n$为实例的特征向量， $y_i \in \mathcal{Y}=\{c_1,c_2,...,c_k\}$为实例的类别， $i=1,2,...,N$；实例特征向量 $x$;
　　输出: 实例$x$所属的类 $y$
　　(1) 根据给点的距离度量，在训练集$T$中找出与 $x$最近邻的$k$个点，涵盖着 $k$个点的领域，记为$N_k(x)$;
　　(2) 在 $N_k(x)$中根据分类决策规则(如多数表决)，决定 $x$的类别$y$:
　　 $y=arg \mathop{\; max}_{c_j} {\sum}_{x_i \in N_k(x)} \; I(y_i=c_j) , i=1,2,...,N;$
　　
　　在上式中， $I$为指示函数，即当$y_i=c_j$时， $I$为1，否则$I$为0。
　　KNN特殊情况是k=1的情形，称为最近邻算法。对于输入的实例点(特征向量) $x$，最近邻算法将训练数据集中与$x$最近邻点的类作为 $x$的类。
　　在KNN算法中，常用的距离有三种，分别为曼哈顿距离、欧式距离和闵可夫斯基距离。
　　设特征空间$\mathcal{X}$是n维实数向量空间 $R_n$, $x_i,x_j \in \mathcal{X}, \quad x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T$, $x_j=(x_j^{(1)},x_j^{(2)},...,x_j^{(n)})^T$, $x_i,x_j$的 $L_p$距离定义为：
　　 $L_p(x_i,x_j) = (\sum_{l=1}^{n} \; |x_i^{(l)}-x_j^{(l)}|^p)^{\frac{1}{p}}$
　　这里 $p \ge 1$
　　当 $p=1$时，称为曼哈顿距离(Manhattan distance), 公式为：
　　 $L_1(x_i,x_j)= \sum_{l=1}^{n} |x_i^{(l)}-x_j^{(l)}|$
　　当 $p=2$时，称为欧式距离(Euclidean distance)，即
　　 $L_2(x_i,x_j) = (\sum_{l=1}^{n} \; |x_i^{(l)}-x_j^{(l)}|^{2})^{\frac{1}{2}}$
　　当 $p=\infty$时，它是各个坐标距离的最大值，计算公式为：
　　 $L_{\infty}(x_i,x_j)= \mathop{max}_l \; |x_i^{(l)}-x_j^{(l)}|$
　　案例1，已知二维空间的3个点 $x_1=(1,1)^T$, $x_2=(5,1)^T$, $x_3=(4,4)^T$, 试求在 $p$取不同值时，$L_p$距离下 $x_1$的最近邻点。
　　解析：对于 $x_1$与 $x_2,$由于 $x_1$与 $x_2在第1维上的数字分别为1、5，$在第2维上 数字都是1，所以计算 $x_1$与 $x_2$的距离时只需计算 $x_1^{(1)}$和 $x_2^{(1)}$即可， $L_p(x_1,x_2)=4$.
　　对于 $x_1$与 $x_3$, 由于 $x_1$与 $x_3$在第1维上的数字不相同，在第2维上的数字也不相同，则 $x_1$与 $x_3$的曼哈顿距离为:
　　 $L_1(x_1,x_3) =\sum_{l=1}^{n} |x_i^{(l)}-x_j^{(l)}| = \sum_{l=1}^{2} |x_i^{(l)}-x_j^{(l)}| =3+3=6$
　　则 $x_1$与 $x_3$的欧式距离为:
　　 $L_2(x_i,x_j) = (\sum_{l=1}^{n} \; |x_i^{(l)}-x_j^{(l)}|^{2})^{\frac{1}{2}}=(\sum_{l=1}^{2} \; |x_i^{(l)}-x_j^{(l)}|^{2})^{\frac{1}{2}} = 3\sqrt{2}=42.4$
　　则 $x_1$与 $x_3$的 $L_3$距离为:
　　 $L_3(x_i,x_j) = (\sum_{l=1}^{n} \; |x_i^{(l)}-x_j^{(l)}|^3)^{\frac{1}{3}} = 3.78$

　　在Matlab，可以直接求两个向量之间的距离。
　　设$x_a=(1,1)$, $x_a=(4,4)$，向量$x_a, \; x_b$组成矩阵D =[1 1; 4 4]
　　（a）求向量(1,1)、(5,1)的曼哈顿距离

D = [1 1; 4 4];
%%求曼哈顿距离
res = pdist(D, 'cityblock')

　　如图(1)所示：

图(1) 使用pdist( XXX , ‘cityblock’)求曼哈顿距离
　　（b）求向量(1,1)、(5,1)的欧式距离
　　在Minkowski distance公式中，当p=2时，就是欧式距离，而Minikowski的函数为 pdist(XXX, ‘minkowski’,2)，代码如下： 　　

D = [1 1; 4 4]
%%求欧式距离
res = pdist(D, 'minkowski',2)

　　如图(2)所示：

图(2) 使用pdist(XXX, ‘minkowski’,2)求曼哈顿距离
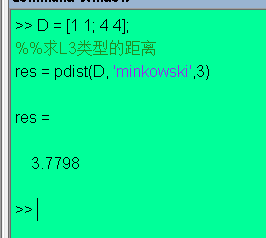
　　（c）求向量(1,1)、(5,1)的 $L_3$距离
　　调用pdist(XXX, ‘minkowski’,3)，代码如下：　　

D = [1 1; 4 4];
%%求L3类型的距离
res = pdist(D, 'minkowski',3)

　　如图(3)所示:

图(3) 求 $L_3$类型的距离