几种常见模式识别算法整理和总结

最新推荐文章于 2024-04-18 19:48:42 发布
最新推荐文章于 2024-04-18 19:48:42 发布
阅读量10w+ 收藏 605
点赞数 56
文章标签： 算法 matrix matlab 数据库 2010 编程
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/scyscyao/article/details/5987581
版权

这学期选了门模式识别的课。发现最常见的一种情况就是，书上写的老师ppt上写的都看不懂，然后绕了一大圈去自己查资料理解，回头看看发现，Ah-ha，原来本质的原理那么简单，自己一开始只不过被那些看似formidable的细节吓到了。所以在这里把自己所学的一些点记录下来，供备忘，也供参考。

 

 

1. K-Nearest Neighbor

K-NN可以说是一种最直接的用来分类未知数据的方法。基本通过下面这张图跟文字说明就可以明白K-NN是干什么的

 

knn

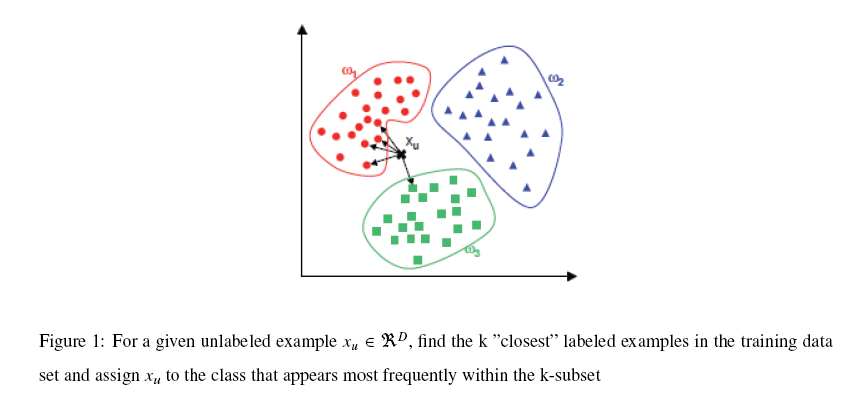
简单来说，K-NN可以看成：有那么一堆你已经知道分类的数据，然后当一个新数据进入的时候，就开始跟训练数据里的每个点求距离，然后挑离这个训练数据最近的K个点看看这几个点属于什么类型，然后用少数服从多数的原则，给新数据归类。一个比较好的介绍k-NN的课件可以见下面链接，图文并茂，我当时一看就懂了

http://courses.cs.tamu.edu/rgutier/cs790_w02/l8.pdf

 

实际上K-NN本身的运算量是相当大的，因为数据的维数往往不止2维，而且训练数据库越大，所求的样本间距离就越多。就拿我们course project的人脸检测来说，输入向量的维数是1024维(32x32的图，当然我觉得这种方法比较silly)，训练数据有上千个，所以每次求距离(这里用的是欧式距离，就是我们最常用的平方和开根号求距法) 这样每个点的归类都要花上上百万次的计算。所以现在比较常用的一种方法就是kd-tree。也就是把整个输入空间划分成很多很多小子区域，然后根据临近的原则把它们组织为树形结构。然后搜索最近K个点的时候就不用全盘比较而只要比较临近几个子区域的训练数据就行了。kd-tree的一个比较好的课件可以见下面链接：

http://www.inf.ed.ac.uk/teaching/courses/inf2b/learnnotes/inf2b-learn06-lec.pdf

当然，kd-tree有一个问题就是当输入维数跟训练数据数量很接近时就很难优化了。所以用PCA(稍后会介绍)降维大多数情况下是很有必要的

 

2. Bayes Classifier
贝叶斯方法一篇比较科普的中文介绍可以见pongba的平凡而神奇的贝叶斯方法:  http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/，实际实现一个贝叶斯分类器之后再回头看这篇文章，感觉就很不一样。
在模式识别的实际应用中，贝叶斯方法绝非就是post正比于prior*likelihood这个公式这么简单，一般而言我们都会用正态分布拟合likelihood来实现。
用正态分布拟合是什么意思呢？贝叶斯方法式子的右边有两个量，一个是prior先验概率，这个求起来很简单，就是一大堆数据中求某一类数据占的百分比就可以了，比如300个一堆的数据中A类数据占100个，那么A的先验概率就是1/3。第二个就是likelihood，likelihood可以这么理解：对于每一类的训练数据，我们都用一个multivariate正态分布来拟合它们(即通过求得某一分类训练数据的平均值和协方差矩阵来拟合出一个正态分布)，然后当进入一个新的测试数据之后，就分别求取这个数据点在每个类别的正态分布中的大小，然后用这个值乘以原先的prior便是所要求得的后验概率post了。
贝叶斯公式中还有一个evidence，对于初学者来说，可能会一下没法理解为什么在实际运算中它不见了。实则上，evidence只是一个让最后post归一化的东西，而在模式分类中，我们只需要比较不同类别间post的大小，归一化反而增加了它的运算量。当然，在有的地方，这个evidence绝对不能省，比如后文提到的GMM中，需要用到EM迭代，这时候如果不用evidence将post归一化，后果就会很可怕。
Bayes方法一个不错的参考网页可见下面链接：


3. Principle Component Analysis
PCA，译为主元分析或者主成份分析，是一种很好的简化数据的方法，也是PR中常见到不能再常见的算法之一。CSDN上有一篇很不错的中文博客介绍PCA，《主元分析(PCA)理论分析及应用》，可以见下面链接：
对于我而言，主元分析最大的意义就是让我明白了线性代数中特征值跟特征向量究竟代表什么，从而让我进一步感受到了线性代数的博大精深魅力无穷。- -|||

PCA简而言之就是根据输入数据的分布给输入数据重新找到更能描述这组数据的正交的坐标轴，比如下面一幅图，对于那个椭圆状的分布，最方便表示这个分布的坐标轴肯定是椭圆的长轴短轴而不是原来的x y。
PCA
那么如何求出这个长轴和短轴呢？于是线性代数就来了：我们求出这堆数据的协方差矩阵(关于什么是协方差矩阵，详见本节最后附的链接)，然后再求出这个协方差矩阵的特征值和特征向量，对应最大特征值的那个特征向量的方向就是长轴(也就是主元)的方向，次大特征值的就是第二主元的方向，以此类推。

关于PCA，推荐两个不错的tutorial:
(1) A tutorial on Principle Component Analysis从最基本的数学原理到应用都有，让我在被老师的讲课弄晕之后瞬间开悟的tutorial:
(2) 里面有一个很生动的实现PCA的例子，还有告诉你PCA跟SVD是什么关系的，对编程实现的帮助很大(当然大多数情况下都不用自己编了):

 http://www.math.ucsd.edu/~gptesler/283/pca_07-handout.pdf

 

4. Linear Discriminant Analysis

LDA，基本和PCA是一对双生子，它们之间的区别就是PCA是一种unsupervised的映射方法而LDA是一种supervised映射方法，这一点可以从下图中一个2D的例子简单看出

lda

图的左边是PCA，它所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上，映射时没有利用任何数据内部的分类信息。因此，虽然做了PCA后，整组数据在表示上更加方便(降低了维数并将信息损失降到最低)，但在分类上也许会变得更加困难；图的右边是LDA，可以明显看出，在增加了分类信息之后，两组输入映射到了另外一个坐标轴上，有了这样一个映射，两组数据之间的就变得更易区分了(在低维上就可以区分，减少了很大的运算量)。


在实际应用中，最常用的一种LDA方法叫作Fisher Linear Discriminant，其简要原理就是求取一个线性变换，是的样本数据中“between classes scatter matrix”(不同类数据间的协方差矩阵)和“within classes scatter matrix”(同一类数据内部的各个数据间协方差矩阵)之比的达到最大。关于Fisher LDA更具体的内容可以见下面课件，写的很不错~

http://www.csd.uwo.ca/~olga/Courses//CS434a_541a//Lecture8.pdf 


 

 

5. Non-negative Matrix Factorization

NMF，中文译为非负矩阵分解。一篇比较不错的NMF中文介绍文可以见下面一篇博文的链接，《非负矩阵分解：数学的奇妙力量》

http://chnfyn.blog.163.com/blog/static/26954632200751625243295/

 

这篇博文很大概地介绍了一下NMF的来龙去脉(当然里面那幅图是错的。。。)，当然如果你想更深入地了解NMF的话，可以参考Lee和Seung当年发表在Nature上面的NMF原文，"Learning the parts of objects by non-negative matrix factorization"

http://www.seas.upenn.edu/~ddlee/Papers/nmf.pdf

读了这篇论文，基本其他任何介绍NMF基本方法的材料都是浮云了。

 

NMF，简而言之，就是给定一个非负矩阵V，我们寻找另外两个非负矩阵W和H来分解它，使得后W和H的乘积是V。论文中所提到的最简单的方法，就是根据最小化||V-WH||的要求，通过Gradient Discent推导出一个update rule，然后再对其中的每个元素进行迭代，最后得到最小值，具体的update rule见下图，注意其中Wia等带下标的符号表示的是矩阵里的元素，而非代表整个矩阵，当年在这个上面绕了好久。。

nmf

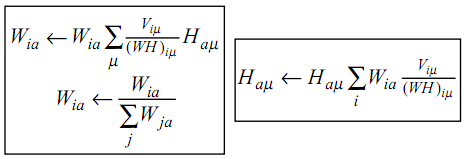
当然上面所提的方法只是其中一种而已，在http://spinner.cofc.edu/~langvillea/NISS-NMF.pdf中有更多详细方法的介绍。

相比于PCA、LDA，NMF有个明显的好处就是它的非负，因为为在很多情况下带有负号的运算算起来都不这么方便，但是它也有一个问题就是NMF分解出来的结果不像PCA和LDA一样是恒定的。

 

6. Gaussian Mixture Model

GMM高斯混合模型粗看上去跟上文所提的贝叶斯分类器有点类似，但两者的方法有很大的不同。在贝叶斯分类器中，我们已经事先知道了训练数据(training set)的分类信息，因此只要根据对应的均值和协方差矩阵拟合一个高斯分布即可。而在GMM中，我们除了数据的信息，对数据的分类一无所知，因此，在运算时我们不仅需要估算每个数据的分类，还要估算这些估算后数据分类的均值和协方差矩阵。。。也就是说如果有1000个训练数据10租分类的话，需要求的未知数是1000+10+10(用未知数表示未必确切，确切的说是1000个1x10标志向量,10个与训练数据同维的平均向量，10个与训练数据同维的方阵)。。。反正想想都是很头大的事情。。。那么这个问题是怎么解决的呢？

这里用的是一种叫EM迭代的方法。


具体使用方法可以参考http://neural.cs.nthu.edu.tw/jang/books/dcpr/doc/08gmm.pdf 这份台湾清华大学的课件，写的真是相当的赞，实现代码的话可以参考：

1. 倩倩的博客http://www.cnblogs.com/jill_new/archive/2010/12/01/1893851.html 和

2. http://www.cs.ru.nl/~ali/EM.m

 

当然 Matlab里一般也会自带GMM工具箱，其用法可以参考下面链接：

http://www.mathworks.com/help/toolbox/stats/gmdistribution.fit.html

 

 

scyscyao
关注
  • 56
    点赞
  • 踩
  • 605
    收藏
    觉得还不错? 一键收藏
  • 27
    评论
模式识别算法
12-13
对模式识别应用的几种算法进行分类整理，分别介绍了各自的优点和不足，对于初学者有个大概的了解比较有用
网管教程 从入门到精通软件篇.txt
04-25
网管教程 从入门到精通软件篇 ★一。★详细的xp修复控制台命令和用法!!! 放入xp（2000）的光盘，安装时候选R，修复！ Windows XP（包括 Windows 2000）的控制台命令是在系统出现一些意外情况下的一种非常有效的诊断和测试以及恢复系统功能的工具。小编的确一直都想把这方面的命令做个总结，这次辛苦老范给我们整理了这份实用的秘笈。 　　Bootcfg 　　bootcfg 命令启动配置和故障恢复（对于大多数计算机，即 boot.ini 文件）。 　　含有下列参数的 bootcfg 命令仅在使用故障恢复控制台时才可用。可在命令提示符下使用带有不同参数的 bootcfg 命令。 　　用法： 　　bootcfg /default　　设置默认引导项。 　　bootcfg /add　　　　向引导列表中添加 Windows 安装。 　　bootcfg /rebuild　　重复全部 Windows 安装过程并允许用户选择要添加的内容。 　　注意：使用 bootcfg /rebuild 之前，应先通过 bootcfg /copy 命令备份 boot.ini 文件。 　　bootcfg /scan　　　 扫描用于 Windows 安装的所有磁盘并显示结果。 　　注意：这些结果被静态存储，并用于本次会话。如果在本次会话期间磁盘配置发生变化，为获得更新的扫描，必须先重新启动计算机，然后再次扫描磁盘。 　　bootcfg /list　　　列出引导列表中已有的条目。 　　bootcfg /disableredirect 在启动引导程序中禁用重定向。 　　bootcfg /redirect [ PortBaudRrate] |[ useBiosSettings] 　　在启动引导程序中通过指定配置启用重定向。 　　范例： bootcfg /redirect com1 115200 bootcfg /redirect useBiosSettings 　　hkdsk 　　创建并显示磁盘的状态报告。Chkdsk 命令还可列出并纠正磁盘上的错误。 　　含有下列参数的 chkdsk 命令仅在使用故障恢复控制台时才可用。可在命令提示符下使用带有不同参数的 chkdsk 命令。 　　vol [drive:] [ chkdsk [drive:] [/p] [/r] 　　参数　　无 　　如果不带任何参数，chkdsk 将显示当前驱动器中的磁盘状态。 drive: 指定要 chkdsk 检查的驱动器。 /p　　 即使驱动器不在 chkdsk 的检查范围内，也执行彻底检查。该参数不对驱动器做任何更改。 /r　　 找到坏扇区并恢复可读取的信息。隐含着 /p 参数。 　　注意 Chkdsk 命令需要 Autochk.exe 文件。如果不能在启动目录（默认为 %systemroot%System32）中找到该文件，将试着在 Windows 安装 CD 中找到它。如果有多引导系统的计算机，必须保证是在包含 Windows 的驱动器上使用该命令。 Diskpart 　　创建和删除硬盘驱动器上的分区。diskpart 命令仅在使用故障恢复控制台时才可用。 　　diskpart [ /add |/delete] [device_name |drive_name |partition_name] [size] 　　参数 无 　　如果不带任何参数，diskpart 命令将启动 diskpart 的 Windows 字符模式版本。 　　/add 　　创建新的分区。 　　/delete 　　删除现有分区。 　　device_name 　　要创建或删除分区的设备。设备名称可从 map 命令的输出获得。例如，设备名称： 　　DeviceHardDisk0 　　drive_name 　　以驱动器号表示的待删除分区。仅与 /delete 同时使用。以下是驱动器名称的范例： 　　D: 　　partition_name 　　以分区名称表示的待删除分区。可代替 drive_name 使用。仅与 /delete 同时使用。以下是分区名称的范例： 　　DeviceHardDisk0Partition1 　　 大小 　　要创建的分区大小，以兆字节 (MB)表示。仅与 /add 同时使用。 　　范例 　　下例将删除分区： diskpart /delete Device HardDisk0 Partition3 diskpart /delete F: 　　下例将在硬盘上添加一个 20 MB 的分区： 　　diskpart /add Device HardDisk0 20 　　Fixboot
模式识别的应用
m0_38012434的博客
02-21 457
总的来说，模式识别在计算机视觉、自然语言处理、医学影像分析、生物特征识别等领域都有广泛的应用，为解决各种实际问题提供了有效的解决方案。模式识别在各种领域都有广泛的应用。
GNU-Makefile中文手册-Ver3.8.pdf
05-27
对“info make”的翻译整理，不是一个纯粹的语言翻译版本，其中对GNU make的一些语法和用法进行了一些详细分析和说明，也加入了一些个人的观点和实践总结。 本书的所有的例子都可以在支持V3.8版本的GNU make的系统中正确执行。 中文于册 伪目标 强制目标(没有命令或依赖的规则) 空目标文件 的特殊目标 多目标 多规则目标 静态模式 静态模式规则的语法 静态模式和隐含规则 双冒号规则 自动产生依赖 第五章:规则的命令 为规则书写命令 命令回显 命令的执行 并发执行命令 命令执行的错误 中断的执行 的递归执行 变量 变量和递归 命令行选项和递归 选项 定义命令包 第六章 中的变量 使用变量 变量的引用 两种变量定义(赋值) 归展开式变量 直接展开式变量 定义一个空格 ”操作符 变量的高级用法 变量的替换引用 变量的套嵌引用 变量取值 如何设置变量 追加变量值 指示符 多行定义 系统环境变量 目标指定变量 模式指定变量 第七章 的条件执行 的条件判断 个例子 条件判断的基本语法 标记测试的条件语句 笫八章:的内嵌函数 的函数 年月日 中文于册 函数的调用语法 文本夂理函数 文件名处理函数 函数 函数 西数 函数 函数 函数 西数 的控制函数 第九章:执行 执行 指定 文件 指定终极日标 替代命令的执行 防止特定文件重建 替换变量定义 使用 进行编译测试 的命令行选项 第十章: 的隐含规则 使用隐含规则 隐含规则的使用 的隐含规则一览 隐含变量 代表命令的变量 命令参数的变量 隐含规则链 模式规 模式规则介绍 模式规则示例 自动化变量 年月日 中文于册 模式的匹配 万用规则 重建内嵌隐含规则 缺省规则 后缀规则 隐含规则搜索算法 笫十一章:使用更新静态库文件 更新静态库文件 库成员作为目标 静态库的更新 更新静态庠的符号索引表 静态库的注意享项 静态库的后缀规则 第十二章: 的特点 的一些特点 源自 的特点 源自其他版本的特点 自身的特点 第十三章和其它版本的兼容 不兼容性 第十四章 的约定 书写约定 基本的约定 规则命令行的约定 代表命令变量 安装目录变量 的标准目标名 安装命令分类 第十五章的常见错误信息 产生的错误信息 附录:关键字索引 可识别的指示符 函数 的自动化变量 环境变量 后序 年月日 中文于册 关于本书 本文瑾献给所有热爱 的程序员!本中文文档版权所有 本文比较完整的讲述 工具,涵盖 的用法、语法。同时重 讨论如何为一个工程编写 作为一个程序员, 工具的使用以及编 写 是必嚅的。系统、详细讲述的中文资料比较少,出于对广大中文 的支持,本人在工作之余,花了个多月时间完成对“ 的翻译整理,完成 这个中文版手册。夲书不是一个纯粹的语言翻译版本,其中对 的一些语法 和用法根据我个人的工作经验进行了一些详细分析和说明,也加入了一些个人的观点和 实践总结。本书的所有的例子都可以在支持版本的 的系统中正确执行。 由于个人水平限制,本文在一些地方存在描述不准确之处。恳请大家在阅读过程中 提出您宝贵的意见,也是对我个人的帮助。我的个人电子邯箱地址: 非常愿意和大家交流!共同学习 阅读本书之前,读者应该对 的工具链和 的一些常用编程工具有一定的 了解。诸如: 等;同时在书写 时,需要能够进行一些 基本的编程。这些工具是维护一个工程的基础。如果大家对这些工具的用法不是 很熟悉,可参考项目资料 阅读本文的几点建议: 如果之前你对 没有了解、当前也不想深入的学习 的读 者。可只阅读本文各章节前半部分的内容(作为各章节的基础知识) 如果你已经对 比较熟悉,你更霄要关心此版本的新增特点、功能、 和之前版本不兼容之处;也可以作为开发过程过程的参考手册。 之前你对 没有概念、或者刚开始接触,本身又想成为一个 下 的专业程序员,那么建议:完整学习本文的各个章节,包括了基础知识和高级 用法、技巧。它会为你在 下的工程开发、工程管理提供非常有用的帮助。 此中文文档当前版本 本文的所有勘误和最新版本可在主 页 上获取!! 谢谢! 徐海兵 年月日 中文于册 第一章:概述 概既述 环境下的程序员如果不会侠用 来构建和管理自己的工程,应该 不能算是一个合柊的专业程序员,至少不能称得上是程序员。在 )环 境下侠用 的 工具能够比较容易的构建一个属于你自己的工程,整个工程的 编译只需要一个命令就可以完成编译、连接以至于最后的执行。不过这需要我们投入 些时间去完成一个或者多个称之为 文件的编写。此文件正是 正常工作 的基础 所要完成的 文件描述了整个工程的编译、连接等规则。其中包括:工程 中的哪些源文件需要编译以及如何编译、需要创建那些库文件以及如何创建这些库文 件、如何最后产生我们想要得可执行文件。尽管看起来可能是很复杂的事情,但是为工 程编写
net学习笔记及其他代码应用
11-16
net的最近面试经典试题ASP.NET面试题集合 1. 简述 private、 protected、 public、 internal 修饰符的访问权限。 答 . private : 私有成员, 在类的内部才可以访问。 protected : 保护成员，该类内部和继承类中可以访问。 public : 公共成员，完全公开，没有访问限制。 internal: 在同一命名空间内可以访问。 2 .列举ASP.NET 页面之间传递值的几种方式。 答. 1.使用QueryString, 如....?id=1; response. Redirect().... 2.使用Session变量 3.使用Server.Transfer 3. 一列数的规则如下: 1、1、2、3、5、8、13、21、34...... 求第30位数是多少， 用递归算法实现。 答：public class MainClass { public static void Main() { Console.WriteLine(Foo(30)); } public static int Foo(int i) { if (i 0 && i <= 2) return 1; else return Foo(i -1) + Foo(i - 2); } } 4.C#中的委托是什么？事件是不是一种委托？ 答 ： 委托可以把一个方法作为参数代入另一个方法。 委托可以理解为指向一个函数的引用。 是，是一种特殊的委托 5.override与重载的区别 答 ： override 与重载的区别。重载是方法的名称相同。参数或参数类型不同，进行多次重载以适应不同的需要 Override 是进行基类中函数的重写。为了适应需要。 6.如果在一个B/S结构的系统中需要传递变量值，但是又不能使用Session、Cookie、Application，您有几种方法进行处理？ 答 ： this.Server.Transfer 7.请编程遍历页面上所有TextBox控件并给它赋值为string.Empty？ 答： foreach (System.Windows.Forms.Control control in this.Controls) { if (control is System.Windows.Forms.TextBox) { System.Windows.Forms.TextBox tb = (System.Windows.Forms.TextBox)control ; tb.Text = String.Empty ; } } 8.请编程实现一个冒泡排序算法？ 答： int [] array = new int ; int temp = 0 ; for (int i = 0 ; i < array.Length - 1 ; i++) { for (int j = i + 1 ; j < array.Length ; j++) { if (array[j] < array) { temp = array ; array = array[j] ; array[j] = temp ; } } } 9.描述一下C#中索引器的实现过程，是否只能根据数字进行索引？ 答：不是。可以用任意类型。 10.求以下表达式的值，写出您想到的一种或几种实现方法： 1-2+3-4+……+m [Page] 答： int Num = this.TextBox1.Text.ToString() ; int Sum = 0 ; for (int i = 0 ; i < Num + 1 ; i++) { if((i%2) == 1) { Sum += i ; } else { Sum = Sum - I ; } } System.Console.WriteLine(Sum.ToString()); System.Console.ReadLine() ; 11.用.net做B/S结构的系统，您是用几层结构来开发，每一层之间的关系以及为什么要这样分层？ 答：一般为3层 数据访问层，业务层，表示层。 数据访问层对数据库进行增删查改。 业务层一般分为二层，业务表观层实现与表示层的沟通，业务规则层实现用户密码的安全等。 表示层为了与用户交互例如用户添加表单。 优点： 分工明确，条理清晰，易于调试，而且具有可扩展性。 缺点： 增加成本。 12.在下面的例子里 using Sy
软件工程-理论与实践(许家珆)习题答案
01-12
习 题 答 案 习题一答案 一、选择题 1. 软件的主要特性是(A B C)。 A) 无形 B) 高成本 C) 包括程序和文档 　　D) 可独立构成计算机系统 2. 软件工程三要素是(C D)。 A) 技术、方法和工具　 B) 方法、工具和过程　 C) 方法、对象和类　 D) 过程、模型、方法 3. 包含风险分析的软件工程模型是(A)。 A) 螺旋模型 B) 瀑布模型 C) 增量模型 D) 喷泉模型 4. 软件工程的主要目标是(C)。 A) 软件需求 　B) 软件设计　 C) 风险分析 　D) 软件实 现 5. 下列属于面向对象开发方法的是(A B C D)。 A) Booch　　 B) UML　 　C) Coad　 　D) OMT 6. 软件危机的主要表现是(B D)。 A) 软件成本太高 B) 软件产品的质量低劣 C) 软件开发人员明显不足 D) 软件生产率低下 7. 软件开发方法的主要工作模型有(A B C) A) 螺旋模型 B) 循环模型 C) 瀑布模型 D) 专家模型 8. 软件工程的目标有(A B C)。 A) 易于维护 B) 低的开发成本 C) 高性能 D) 短的开发期 9. 软件工程学的目的和意义是( )。 A) 应用科学的方法和工程化的规范管理来指导软件开发 B) 克服软件危机 C) 作好软件开发的培训工作 D) 以较低的成本开发出高质量的软件 二、 判断题 1. 软件就是程序，编写软件就是编写程序。(×) 2. 瀑布模型的最大优点是将软件开发的各个阶段划分得十分清晰。(×) 3. 结构化方法的工作模型是使用螺旋模型进行开发。(×) 4. 结构化方法和JSP方法都不适合于大型软件的开发。(√) 5. 原型化开发方法包括生成原型和实现原型两个步骤。(×) 6. 面向对象的开发方法包括面向对象的分析、面向对象的设计和面向对象的程序设计。( √) 7. 软件危机的主要表现是软件的需求量迅速增加，软件价格上升。(×) 8. 软件工具的作用是为了延长软件产品的寿命。(×) 9. 软件工程过程应该以软件设计为中心，关键是编写程序。(×) 10. RCP法与RSP法的主要区别是前者采用循环渐进的开发方式，原型将成为最终的产品，而后者将被废弃。(√) 三、简答题 1. 软件产品的特性是什么？ 答： ●　软件是一种逻辑产品，具有无形性； 　●　软件产品的生产主要是研制； 　●　软件不存在磨损和老化问题，但存在退化问题； 　●　软件产品的生产主要是脑力劳动； 　●　软件产品的成本非常昂贵，其开发方式目前尚未完全摆脱手工生产方式； ● 软件具有“复杂性”，其开发和运行常受到计算机系统的限制。 2. 软件发展有几个阶段？各有何特征？ 答： ① 程序设计阶段。 　　　硬件特征：价格贵、存储容量小、运行可靠性差。 　　　软件特征：只有程序、程序设计概念，不重视程序设计方法。 　　② 程序系统阶段。 　　　硬件特征：速度、容量及工作可靠性有明显提高，价格降低，销售有爆炸性增长 。 　　　软件特征：程序员数量猛增，开发人员素质低。 　　③ 软件工程阶段。 　　　硬件特征：向超高速、大容量、微型化及网络化方向发展。 　　　软件特征：开发技术有很大进步，但未获得突破性进展，软件价格不断上升，未完全摆脱软件危机。 3. 什么是软件危机？其产生的原因是什么？ 答：“软件危机”(Software Crisis)的出现是由于软件的规模越来越大，复杂度不断增 加，软件需求量增大。而软件开发过程是一种高密集度的脑力劳动，软件开发的模式及技术 不能适应软件发展的需要。致使大量质量低劣的软件涌向市场，有的花费大量人力、财力， 而在开发过程中就夭折。软件危机主要表现在两个方面： (1) 软件产品质量低劣，甚至开发过程就夭折。 (2) 软件生产率低，不能满足需要。 4. 什么是软件生存周期模型？它有哪些主要模型？ 答：软件生存周期模型是描述软件开发过程中各种活动如何执行的模型。 主要模型包括：瀑布模型、增量模型、螺旋模型、喷泉模型、变换模型和基于知识的模型。 5. 有哪些主要的软件开发方法？ 答：主要的软件开发方法有：结构化开发方法、Jackson(JSP、JSD)方法、原型化开发方 法、维也纳开发方法(VDM)和面向对象的开发方法。 6. 软件生命期各阶段的任务是什么？ 答：软件生命期瀑布模型分为六个阶段： ● 可行性研究与计划(确定系统的目标和规模，分析项目的可行性)； ● 需求分析与规格说明(明确系统的规格和要求)； ● 设计(包括概要设计和详细设计，将系统分解为模块)； ● 编程(用程序语言实现每个模块，简单容易)； ● 测试(发现并改正错误，分为模块测试、集成测试和系统联调三级)； ● 运行维护(扩充功能、纠错等)。 习题二答案 一、 选择题 1. 需求分析的主要目的是(Ｂ Ｃ)。 A) 系统开发的具体方案 B) 进一步确定用户的需求 C) 解决系统是“做什么的问题” D) 解决系统是“如何做的问题” 2. 需求分析的主要方法有(Ｃ Ｄ)。 A) 形式化分析方法 B) PAD图描述 C) 结构化分析(SA)方法 D) OOA法 3. 面向对象的分析方法主要是建立三类模型，即(Ｄ)。 A) 系统模型、ER模型、应用模型 B) 对象模型、动态模型、应用模型 C) Ｅ-Ｒ模型、对象模型、功能模型 D) 对象模型、动态模型、功能模型 4. ＳＡ法的主要描述手段有(Ｂ)。 A) 系统流程图和模块图 B) ＤＦＤ图、数据词典、加工说明 C) 软件结构图、加工说明 D) 功能结构图、加工说明 5. 画分层ＤＦＤ图的基本原则有(Ａ Ｃ Ｄ)。 A) 数据守恒原则 B) 分解的可靠性原则 C) 子、父图平衡的原则 D) 数据流封闭的原则 6. 在E-R模型中，包含以下基本成分(C)。 A) 数据、对象、实体 B) 控制、联系、对象 C) 实体、联系、属性 D) 实体、属性、联系 7. 画DFD图的主要目的是(A D)。 A) 作为需求分析阶段用户与开发者之间交流信息的工具 B) 对系统的数据结构进行描述 C) 对目标系统的层次结构进行描述 D) 作为分析和设计的工具 8. 数据字典是数据流图中所有元素的定义的集合，一般由以下四类条目组成(C)。 A) 数据说明条目、控制流条目、加工条目、数据存储条目 B) 数据流条目、数据项条目、文件条目、加工条目 C) 数据源条目、数据流条目、数据处理条目、数据文件条目 D) 数据流条目、数据文件条目、数据池条目、加工条目 9. 在需求分析阶段主要采用图形工具来描述的原因是(B C)。 A) 图形的信息量大，便于描述规模大的软件系统 B) 图形工具能够极好地概括描述一个系统的信息，比文字叙述能够更好地表达重 要的细节 C) 图形能够更加直观地描述目标系统，便于用户理解和交流，有利于开发者与用 户之间达成一致的需求 D) 图形比文字描述简单、形象 二、 判断题 1. 在进行了可行性分析后，需求分析就只需要解决目标系统的设计方案。(×) 2. ＳＡ法是面向数据流，建立在数据封闭原则上的需求分析方法。(√) 3. HIPO法既是需求分析方法，又是软件设计方法。(√) 4. 在面向对象的需求分析方法中，建立动态模型是最主要的任务。(×) 5. 加工小说明是对系统流程图中的加工进行说明。(×) 6. 判定表的优点是容易转换为计算机实现，缺点是不能够描述组合条件。(×) 7. 需求分析的主要方法有SD法、OOA法及HIPO法等。(×) 8. 分层的DFD图可以用于可行性分析阶段，描述系统的物理结构。(×) 9. 信息建模方法是从数据的角度来建立信息模型的，最常用的描述信息模型的方法是E-R 图。(√) 　10. 用于需求分析的软件工具，应该能够保证需求的正确性，即验证需求的一致性、完整性、现实性和有效性。(√) 三、 问答题 1. 什么是需求分析？需求分析阶段的基本任务是什么？ 答： 需求分析是当前软件工程中的关键问题，需求分析阶段的任务是：在可行性分析的基础上，进一步了解、确定用户需求。准确地回答 “系统必须做什么？” 的问题。获得需求规格说 明书。还涉及到软件系统的目标、软件系统提供的服务、软件系统的约束和软件系统运行的环境。它还涉及到这些因素和系统的精确规格说明，以及系统进化之间的关系。 需求分析的基本任务包括： (1) 抽取需求 分析现行系统存在需要解决的问题。获取足够多的问题领域的知识，需求抽取的方法一般有问卷法、面谈法、数据采集法、用例法、情景实例法以及基于目标的方法等；还有知识工程方法，例如，场记分析法、卡片分类法、分类表格技术和基于模型的知识获取等 。 (2) 模拟和分析需求 需求分析和模拟又包含三个层次的工作。首先是需求建模。需求模型的表现形式有自然语言、半形式化(如图、表、结构化英语等)和形式化表示等三种。需求概念模型的要求包括实现的独立性:不模拟数据的表示和内部组织等；需求模拟技术又分为企业模拟、功能需求模拟和非功能需求模拟等。 (3) 传递需求 传递需求的主要任务是书写软件需求规格说明。 (4) 认可需求 就是对需求规格说明达成一致，其主要任务是冲突求解，包括定义冲突和冲突求解两方面。常用的冲突求解方法有：协商、竞争、仲裁、强制、教育等，其中有些只能用人的因素去控制。 (5) 进化需求 客户的需要总是不断(连续)地增长，但是一般的软件开发又总是落后于客户需求的增长，如何管理需求的进化(变化)就成为软件进化的首要问题。对于传统的变化管理过程来说，其基本成分包括软件配置、软件基线和变化审查小组。当前的发展是软件家族法 ，即产品线方法。多视点方法也是管理需求变化的一种新方法，它可以用于管理不一致性， 并进行关于变化的推理。 2. M公司的软件产品以开发实验型的新软件为主。用瀑布模型进行软件开发已经有近十年了，并取得了一些成功。若你作为一名管理员刚加入M公司，你认为快速原型法对公司的软件开发更加优越，请向公司副总裁写一份报告阐明你的理由，切记：副总裁不喜欢报告长度 超过一页(B5)。 参考答案提示： 应先简述瀑布模型的缺点，它已不适宜开发实验型的软件。根据快速原型法的特点，说明它特别适合于开发探索型、实验型的软件。 3. 如何画分层数据流图？ 答： 总的原则是：至顶而下，逐层分解(画分层数据流图)。 比较复杂的系统不能画在一张纸上，逐层分解的画法可以控制每一层的复杂度。 顶层：将整个系统作为一个加工，描述系统边界(输入与输出)。 中间层：表示某个加工分解为一组子加工，其中的子加工还需进一步分解。 底层：由不再进行分解的基本加工组成。 4. 加工小说明有哪些描述方法？ 答： ●　结构化语言：介于自然语言和形式语言(如谓词逻辑)之间。 ●　结构化英语：通常由外层和内层结构组成。 ●　汉语的情况：精确、简明扼要、文体可以灵活。 ●　判定表：适用于表述比较复杂的加工逻辑，如具有多项选择条件的操作。 ●　判定树：本质上与判定表相同，图形表示更易于理解。 5. 考察下图中子图、父图的平衡。 图1 图2 参考答案： 图1中子图与父图不平衡。子图是父图中加工2的分解，加工2 有输入数据流M和N，输出数据流T，而子图则只有一个输入数据N，却有两个输出数据流T与S。 图2中子图是父图中加工3的分解，虽然表面上加工3只有一个输入数据流“订货单”，而子图却有三个输入数据流，但是如果“订货单”是由“客户”、“账号”和“数量”三部分组成，即有如下数据条目，订货单=客户+账号+数量（2.2.5数据词典），则子、父图平衡。 6. 画出银行取款过程的DFD图。问题描述为：储户用存折取款，首先填写取款单，根据“ 账卡”中的信息检验取款单与存折，如有问题，将问题反馈给储户，否则，登录“储户存款 数据库”，修改相应数据，并更新“账卡”，同时发出付款通知，出纳向储户付款。 参考答案： 7. 常用的软件需求分析方法有哪些？ 答： 结构化分析方法(SA)、功能分解法、信息建模法、面向对象的分析方法(OOA)。 习题三答案 一、 选择题 1. 模块的基本特征是(A C)。 A) 外部特征(输入/输出、功能) B) 内部特征(输入/输出、功能) C) 内部特征(局部数据、代码) D) 外部特征(局部数据、代码 ) 2. SD方法的设计总则是(C D)。 A) 程序简洁、操作方便 B) 结构清晰、合理 C) 模块内聚性强 D) 模块之间耦合度低 3. 软件设计的主要任务是(A B D)。 A) 将分析阶段获得的需求说明转换为计算机中可实现的系统 B) 完成系统的数据结构和程序结构设计 C) 完成模块的编码和测试 D) 对模块内部的过程进行设计 4. 设计阶段应达到的目标有(Ａ Ｄ)。 A) 提高可靠性和可维护性 B) 提高应用范围 C) 结构清晰 D) 提高可理解性和效率 5. 从工程管理的角度来看，软件设计分两步完成(D)。 A) ①系统分析②模块设计 B) ①详细设计②总体设 计 C) ①模块设计②详细设计 D) ①总体设计②详细设 计 6. 模块独立性准则由以下定性指标来衡量(ＢＤ)。 A) 分解度　　　 B) 耦合度　 　 C) 屏蔽性　　 　D) 内聚性 7. 用户界面设计的任务包括(A B C)。 A) 确定用户界面类型 B) 建立任务模型 C) 建立用户模型 D) 建立功能模型 8. 程序设计语言可以分为(B C D)。 A) 面向过程的语言　　　 B) 机器语言 C) 高级语言　　　 D) 汇编语言　 9. 程序效率包括(A C D)几个方面的内容。 A) 代码效率　　　　 B) 运行效率　　　　C) 存储效率　　 　 D) I/O效率 10. SP方法中的基本控制结构有(A B C)。 A) 顺序结构 B) 选择结构 C) 重复结构 D) GOTO结构 11. 内部文档可用注释语言书写，注释语言分为(A B C D)。 A) 序言性注释 B) 描述性注释 C) 功能性注释 D) 状态性注释 12. 为使程序中数据说明更易于理解和维护，必须遵循以下原则(A B C) 。 A) 数据说明的次序应当规范化 B) 一个语句说明多个变量时，各变量名按字母顺序排列 C) 对于复杂的数据结构，要加注释，说明在程序实现时的特点 D) 定义变量名应按字母顺序排列 13. 源程序的效率与(D)阶段确定的算法的效率直接有关。 A) 概要设计 B) 总体设计 C) 单元设计 D) 详细设计 14. 在详细设计翻译转换成源程序代码后，算法效率反映为对程序的哪几个方面的要求 (C D)。 A) 读写速度 B) 代码长度 C) 存储容量 D) 执行速度 15. 提高程序效率的根本途径在于(B C)。 A) 编程时对程序语句进行调整 B) 选择良好的设计方法 C) 使程序最大限度的简洁 D) 选择良好的数据结构与算法 二、判断题 1. 划分模块可以降低软件的复杂度和工作量，所以应该将模块分得越小越好。 (×) 2. 在网状结构中任何两个模块都是平等的，没有从属关系，所以在软件开发过程中常常被使用。(×) 3. 信息隐蔽原则有利于提高模块的内聚性。(√) 4. 中心变换型的DFD图可看成是对输入数据进行转换而得到输出数据的处理，因此可以使 用事务分析技术得到初始的模块结构图。(×) 5. SD法是一种面向数据结构的设计方法，强调程序结构与问题结构相对应。 (×) 6. 所谓结构冲突，是指输入数据与输出数据之间很少或没有结构上的对应关系。通常解决 的办法是：构造一个或者多个中间结构，在输入和输出结构之间进行转换。(√) 7. 当模块的控制范围是其作用范围的子集时，模块之间的耦合度较低。(×) 8. JACKSON方法是以数据流、数据封闭性准则逐层分解的。(×) 9. 程序设计语言的工程特性包括：可移植性、可重用性、可维护性、局部性和顺序性。(×) 10. 项目应用领域是选择语言的关键因素。(√) 11. FORTRAN、Pascal、C语言、PL/1和汇编语言都是科学工程计算可选用的语言。(×) 12. 要用快速原型法开发软件，应选用4GL语言。(√) 13. 提高程序效率的根本途径是选择良好的设计方法、数据结构与算法。(×) 14. 良好的程序设计风格简单说就是高的编程技巧。(√) 三、简答题 1. 模块内联系和模块间联系有哪些种类? 答：块间联系的各种类型的划分，从以下3方面考虑： ● 按块间联系的方式（可分为直接引用与过程调用）； ● 按块间共用信息的作用（可分为数据型、控制型与混合型）； ● 按块间共用的信息数量多少（信息多联系紧密）。 （1） 块间联系的类型，按照耦合度由大到小分为： 内容型：直接引用另一模块的内部信息； 公共型：两个模块引用共同的全程数据区； 控制型：模块间传送的信息用于控制模块的内部逻辑； 复合型：模块间传送复合的数据结构； 数据型：模块间传送单个数据项。 （2） 块内联系的类型，按照内聚性从小到大分为： 偶然型：模块内部没有必然联系； 逻辑型：逻辑上相似的功能放进一个模块； 瞬时型：将同时执行的语句放在一个模块； 通信型：模块中的各部分引用共同的数据； 顺序型：模块中一部分的输出是另一部分的收入； 功能型： 模块中刚好包含了完成一个基本任务所必需的成分。 2. 分析以下DFD图，说明属于哪种类型的DFD图，并按照相应的变换将其转换为初始的模块 结构图。 参考答案：(略) 3. 下图是修改文件记录的DFD图，请确定其主加工。 解：主加工为：账号、修改、写记录。 4. 按照“降低块间联系，提高块内联系”的设计总则对模块进行修改，具体从哪些方面进 行改进？ 解： (1) 尽可能建立功能模块； (2) 消除重复功能； (3) 模块的作用范围与控制范围，即当作用范围为控制范围的子集时，才能获得较低的块间 联系； (4) 模块的大小适当； (5) 模块的扇入扇出数不宜太多。 5. 根据模块的作用范围与控制范围的原则，判定a、b两图的正确性。 解：显然，图a不满足作用范围应与控制范围的原则，模块F的作用范围不在控制范围之内。 图b的模块设计合理。 6. 图a中，模块G为判定，判断涉及到模块B、F、G，请指出设计中的错误，再根据改进模 块图的基本原则，画出1～2个改进方案(不改变模块G的判断关系)，并说明是按照哪条基本 原则进行改进的。 解：图b为一个改进方案，将模块G的位置提高，使其作用范围为控制范围的子集，减少模块 之间的联系。 7. 编码阶段的主要任务是什，应交付的结果是什么？ 答：编码阶段的主要任务是为每个模块编写程序。即是：将详细设计的结果转换为用某种计 算机语言写的程序——源程序代码。编码阶段应交付的结果是带有“程序内部文档”的、不 再含有语法错误的程序。 8. SP法的自顶向下，逐步求精方法的优点有哪些？ 答：此法符合人们解决复杂问题的普遍规律，可提高软件开发的成功率和生产率；而且用先 全局后局部、先整体后细节、先抽象后具体的逐步求精过程，开发出来的程序具有清晰的层 次结构，因此程序容易阅读和理解。这样，程序自顶向下，逐步细化，分解成一个树型结构 。 因此，在同一层次的节点上做细化工作，相互之间没有联系，它们之间的细化工作相互独立 ；在任何一步发生错误，一般只影响它下层的节点，同一层其他节点不受影响；在以后的测试中，也可以先独立地一个节点一个节点地做，最后再集成。这样，程序清晰和模块化，使 得在修改和重新设计一个软件时，可复用的代码量最大。 9. 为了使程序具有良好的设计风格，应注意哪些方面的问题？ 答：(1) 标识符应按意取名。 标识符即符号名，包括：模块名、常量名、标号名、子程序名、数据区名、缓冲区名等。 这些名字应能反映它所代表的实际东西，应有一定实际意义，使其能够见名知意，有助于对 程序功能的理解。 (2) 程序应加注释，它分为两类：序言性注释和功能性注释。 序言性注释应置于每个模块的起始部分，主要内容有：①说明每个模块的用途，功能；②说明模块的接口即调用格式、参数描述及从属模块的清单；③数据描述；④开发历史 。 功能性注释是嵌在源程序体中的，用于说明其后的程序段或语句的功能以及数据的状态；也就是解释下面要“做什么”，或是执行下面的语句会发生什么情况；而不是解释下面“怎么做”，因为怎么做常常是与程序重复的，且对读者理解程序没有什么帮助。 10. 样评价程序的执行效率？它与程序清晰性的关系是怎样的？ 答：许多程序员往往片面追求效率，其实程序系统的成本不仅包括运行所需的机时，同时还应把程序员及操作员所花费的人力考虑进去。在编程时为追求效率而损害可读性或可靠性，会给以后的维护工作带来困难，所以从整体上看来是不值得的。 此外，还应该认识到，提高程序效率的根本途径在于：选择良好的设计方法、良好的数据结构与算法，而不是靠编程时对程序语句进行调整。 (1) 追求建立在不损害程序可读性或可靠性基础上，要先使程序正确、清晰，再提高程序 效率。 (2) 不能因为贪图效率上的小利，而破坏程序的清晰性。 (3) 让编译程序去作简单的优化。 (4) 提高程序效率的根本途径在于：选择良好的设计方法和良好的数据结构与算法，而不是靠编程时对程序语句做调整。 11. 假定：需要编一个求解一元二次方程根的子程序，加入到现有的子程序库中，供其他程序员使用。要求： (1) 为该子程序写一个序言性注释； (2) 用PASCAL语言或其他语言写出这个子程序(要把根的性质，如：实根、复根、降为一次方程等有区别地通知调用者)，并加上描述性注释。 答案：(略) 习题四答案 一、选择题 1. 面向对象程序设计的基本机制(ABC)。 A) 继承 B) 消息 C) 方法 D) 结构 2. 下列属于面向对象的要素有(BCD)。 A) 分类性 B) 抽象 C) 共享 D) 封装 3. 下列选项中属于面向对象开发方法的有(ACD)。 A) Booch B) CAD C) Coad D) OMT 4. 下列属于Coad方法中面向对象的分析模型的层次有(AB)。 A) 主题层 B) 对象层 C) 应用层 D) 接口层 5. 一个类属性依其特征划分，其类型有(ABCD)。 A) 描述型 B) 定义型 C) 派生型 D) 参考型 6. 在进行面向对象分析时，所采用的模型有(ABD)。 A) 对象模型 B) 动态模型 C) 静态模型 D) 功能模型 7. 状态是对象属性的值的一种抽象，它的性质有(AB)。 A) 时间性 B) 持续性 C) 有序性 D) 有穷性 8. 数据流图中的处理必须用对象中的操作来实现常见的操作有(ABCD)。 A) 查询 B) 动作 C) 活动 D) 访问 9. 建立继承关系时所采用的方式有(AC)。 A) 自顶向下 B) 从内到外 C) 自底向上 D) 从复杂到简单 10. 对象是人们要研究的任何事物主要的对象类型有(ABCD)。 A) 有形实体 B) 作用 C) 事件 D) 性能说明 二、判断题 1. 面向对象的的方法是以类作为最基本的元素，它是分析问题解决问题的核心。(×) 2. 类是指具有相同或相似性质对象的抽象，对象是抽象的类，类的具体化就是对象。(√) 3. 继承性是父类和子类之间共享数据结构和消息的机制，这是类之间的一种关系(×)。 4. 多态性增强了软件的灵活性和重用性，允许用更为明确、易懂的方式去建立通用软件， 多态性和继承性相结合使软件具有更广泛的重用性和可扩充性。(×) 5. 面向对象分析，就是抽取和整理用户需求并建立问题域精确模型的过程。(√) 6. 面向对象的设计的主要目标是提高生产效率，提高质量和提高可维护性。(√) 7. 对象模型表示了静态的、结构化的系统数据性质，描述了系统的静态结构，它是从客观世界实体的对象关系角度来描述，表现了对象的相互关系。(√) 8. 面向对象的分析是用面向对象的方法对目标系统的问题空间进行理解、分析和反映。通过对象层次结构的组织确定解空间中应存在的对象和对象层次结构。(√) 9. 类的设计过程包括：确定类,确定关联类,确定属性,识别继承关系。(√) 10. 复用也叫重用或再用，面向对象技术中的“类”，是比较理想的可重用软构件。有三种重用方式：实例重用、继承重用、多态重用。(√) 11. 主题是一种关于模型的抽象机制，它是面向对象模型的概貌，也是关于某个模型要同时考虑和理解的内容，主题起一种控制作用。(√) 12. 面向对象的分析由对象、结构、继承性和基于消息的通信构成。(×) 13. 支持继承性是面向对象程序设计语言和传统程序设计语言在语言机制方面的根本区别。(√) 14. 面向对象的分析过程主要包括三项内容：理解、表达和验证。(√) 15. 面向对象的设计的主要目标是提高生产效率、提高质量和提高可维护性。(√) 三、 简答题 1． 与传统程序设计模式中的过程调用相比，消息传递机制有何本质区别？ 答： (1) 消息传递必须给出信道的信息，通常要指出明显的接受方。 (2) 由于接受方是一通信实体，具有保持状态的能力，所以同一发送方在不同时刻向同一 接受方发送同样的信息，可因接受方的当前状态不同而得到不同的结果。 (3) 消息传递可以是异步的，发送方可以不必等待接受方返回信息就可以继续执行后面的操作，因而支持程序的并发和分布执行，而过程调用只能是同步的，本质上是串行的。 2． 阐述面向对象的特征，并做简要的解释。 答： (1) 对象惟一性。 每个对象都有自身惟一的标识，通过这种标识，可找到相应的对象。 (2) 分类性。 是指将具有一致的数据结构(属性)和行为(操作)的对象抽象成类。 (3) 继承性。 是父类和子类之间共享数据结构和方法的机制，这是类之间的一种关系。 (4) 多态性。 是指相同的操作或函数，过程作用于多种类型的对象上，并获得不同的结果。 3． Coad方法主要由面向对象分析OOA和面向对象设计OOD。OOA方法分析过程和构造OOA概念模型的顺序由5个层次组成，请简述这5个层次。 答： (1) 发现类及对象。描述如何发现类及对象。从应用领域开始识别类及对象，形成整 个应用的基础，然后，据此分析系统的责任。 (2) 识别结构。该阶段分为两个步骤。第一，识别“一般－特殊”结构，该结构捕获了识别出的类的层次结构；第二，识别“整体－部分”结构，该结构用来表示一个对象如何成为另一个对象的一部分，以及多个对象如何组装成更大的对象。 (3) 定义主题。主题由一组类及对象组成，用于将类及对象模型划分为更大的单位，便于理解。 (4) 定义属性。其中包括定义类的实例(对象)之间的实例连接。 (5) 定义服务。其中包括定义对象之间的消息连接。 4． 面向对象程序设计有哪些优点？ 解：开发时间短、效率高、可靠性高，所开发的程序更强壮。由于面向对象编程的可重用性 ，可以在应用程序中大量采用成熟的类库，从而缩短开发时间，这样程序更易于维护、 更新和升级。继承和封装使得应用程序的修改带来的影响更加局部 化。 5．比较面向对象方法与结构化方法的特点。 解：分析是问题抽象 (做什么)，设计是问题求解 (怎么做)，实现是问题的解 (结果)。任 何方法学对客观世界的抽象和求解过程都是如此。在问题抽象阶段，结构化方法面向过程， 按照数据变换的过程寻找问题的结点，对问题进行分解。因此，与面向对象方法强调的对象 模型不同，描述数据变换的功能模型是结构化方法的重点。如果问题世界的功能比数据更复 杂或者更重要，那么结构化方法仍然应是首选的方法学。如果数据结构复杂且变换不多， 那么如果以过程主导分析和设计，一旦有系统变更就会给下游开发带来极大混乱。 由于对过程的理解不同，面向过程的功能细分所分割出的功能模块有时会因人而异。而面向 对象的对象细分，从同一问题领域的对象出发，不同人得出相同结论的比率较高。 在设计上，结构化方法学产生自顶向下、结构清晰的系统结构。每个模块有可能保持较强的独立性，但它往往与数据库结构相独立，功能模块与数据库逻辑模式间没有映射关系，程序与数据结构很难封装在一起。如果数据结构复杂，则模块独立性很难保证。面向对象方法抽象的系统结构往往并不比结构化方法产生的系统结构简单，但它能映射到数据库结构中，很容易实现程序与数据结构的封装。 在软件工程基本原则中有一条“形式化原则”，即对问题世界的抽象结论应该以形式化语言 (图形语言、伪码语言等)表述出来。结构化方法可以用数据流图、系统结构图、数据辞典、状态转移图、实体关系图来进行系统逻辑模型的描述；而面向对象方法可以使用对象模型图、数据辞典、动态模型图、功能模型图。其中对象模型图近似系统结构图与实体关系图的结合，动态模型图类似状态迁移图，功能模型图类似数据流图。 6．当重要的对象被发现后，通过一组互相关联的模型详细表示类之间的关系和对象的行为，这些模型从四个不同的侧面表示了软件的体系结构、静态逻辑、动态逻辑、静态物理和动态物理。试描述一下这四种特性。 解：静态逻辑模型描述实例化(类成员关系)、关联、聚集(整体/部分)、和一般化(继承)等关系。这被称为对象模型。一般化关系表示属性和方法的继承关系。定义对象模 型的图形符号体系通常是从用于数据建模的实体关系图导出的。对设计十分重要的约束，如 基数(一对一、一对多、多对多)，也在对象模型中表示。 动态逻辑模型描述对象之间的互相作用。互相作用通过一组协同的对象，对象之间消 息的有序的序列，参与对象的可见性定义，来定义系统运行时的行为。 静态物理模型通过模块描述代码的布局。动态物理模型描述软件的进程和线程体系结 构。 习题五答案 一、选择题 1. 下列不是模型元素的是（D）。 A) 关联 B) 聚合 C) 依赖 D) 笔记 2. UML具有扩展性，常见的扩展机制有（BCD）。 A) 修饰 B) 版类 C) 加标签值 D) 约束 3. UML语言支持的建模方式有（ABD）。 A) 静态建模 B) 动态建模 C) 模块化建模 D) 功能建模 4. 下列各种图可用于动态建模的有（ACD）。 A) 状态图 B) 类图 C) 序列图 D) 活动图 5. 下列属于状态的组成部分的有（AB）。 A) 名称 B) 活动 C) 条件 D) 事件 6. UML中包括的事件有（ABCD）。 A) 条件为真 B) 收到另一对象的信号 C) 收到操作调用 D) 时间表达式 7. 属性的可见性有（ABD）。 A) 公有的 B) 私有的 C) 私有保护的 D) 保护的 8. 用例之间的关系有（BCD）。 A) 友元 B) 扩展 C) 使用 D) 组合 9. 应用于通用化约束的方式有（ABCD）。 A) 完整 B) 不相交 C) 不完整 D) 覆盖 10. 消息的类型有（ABC）。 A) 同步 B) 异步 C) 简单 D) 复杂 二、 判断题 1. UML建模语言是由视图、图、模型元素和通用机制构成的层次关系来描述的。 (√) 2. UML是一种建模语言，是一种标准的表示，是一种方法。 (×) 3. 泳道是一种分组机制，它描述了状态图中对象所执行的活动。 (×) 4. 同步消息和异步消息的主要区别是：同步消息的发送对象在消息发送后，不必等待消息处理，可立即继续执行，而异步消息则发送对象必须等待接收对象完成消息处理后，才能继续执行。 (×) 5. 类图中的角色是用于描述该类在关联中所扮演的角色和职责的。 (√) 6. 类图用来表示系统中类和类与类之间的关系，它是对系统动态结构的描述。 (×) 7. 用例模型的基本组成部件是用例、角色和用例之间的联系。 (√)
模式识别概念
weixin_44734502的博客
09-03 5420
模式识别概念、目的、方法、基本构成、性能测试
模式识别的几种基本算法
woshiliulei0的专栏
06-10 6573
本学期选了模式识别的课程，该期末考试了， 将本课程的几种基本算法整理一下。  1.最近邻算法 （1）最近邻算法：为了判定未知样本的类别，以全部训练样本作为代表点，计算未知样本与所有训练样本的距离，并以最近邻者的类别作为决策未知样本类别的唯一依据。  （2）公式表达：对于S类别问题，每类有Ni个样本，则第i类的识别函数是(i=1,2,…S) 2.
模式识别
知识搬运工的博客
07-08 2032
对于时间和空间中可观察的物体，如果我们可以区分它们是否相同或相似，都可以称之为“模式”（或“模式类”）。模式所指的不是事物本身，而是从事物中获得的信息。因此，模式常常表现为具有时间和空间分布的信息。模式的直观特性包括：可观察性，可区分性，相似性。 模式识别就是对模式的区分和认识，把对象根据其特征归到若干类别中的适当一类。 模式识别并不是根据物体本身来判断的，而是根...
什么是模式识别，模式识别主要识别什么？
热门推荐
数智集的博客
03-20 6万+
模式识别诞生于20实际20年代，随着40年代计算机的出现，50年代人工智能的兴起，模式识别在60年代初迅速发展成为一门学科。简单点说，模式识别是根据输入的原始数据对齐进行各种分析判断，从而得到其类别属性，特征判断的过程。为了具备这种能力，人类在过去的几千万年里，通过对大量事物的认知和理解，逐步进化出了高度复杂的神经和认知系统。举例来说，我们能够轻易的判别出哪个是钥匙、哪个是锁，哪个是自行车、哪个是...
模式识别：第一章 概论
fan1102958151的博客
07-05 1611
模式识别：通过对模式的认识和区分来认识对象，并能够对对象进辨别和分类。
Reversing:逆向工程揭密
06-21
第三卷************** 不错的PDF电子书，共3个分卷，点我名字可以找全 第1部分 逆向101 第1章 基础 3 1.1 什么是逆向工程 3 1.2 软件逆向工程：逆向 4 1.3 逆向应用 4 1.3.1 与安全相关的逆向 5 1.3.2 软件开发中的逆向 8 1.4 底层软件 9 1.4.1 汇编语言 10 1.4.2 编译器 11 1.4.3 虚拟机和字节码 12 1.4.4 操作系统 13 1.5 逆向过程 13 1.5.1 系统级逆向 14 1.5.2 代码级逆向 14 1.6 工具 14 1.6.1 系统监控工具 15 1.6.2 反汇编器 15 1.6.3 调试器 15 1.6.4 反编译器 16 1.7 逆向合法吗？ 17 1.7.1 互操作性 17 1.7.2 竞争 18 1.7.3 版权法 19 1.7.4 商业机密和专利权 20 1.7.5 美国数字千禧版权法 20 1.7.6 DMCA案例 22 1.7.7 许可证协议 23 1.8 代码范例与工具 23 1.9 结论 23 第2章 底层软件 25 2.1 高阶视角 26 2.1.1 程序结构 26 2.1.2 数据管理 29 2.1.3 控制流 32 2.1.4 高级语言 33 2.2 低阶视角 37 2.2.1 底层数据管理 37 2.2.2 控制流 43 2.3 汇编语言101 44 2.3.1 寄存器 44 2.3.2 标志位 46 2.3.3 指令格式 47 2.3.4 基本指令 48 2.3.5 范例 52 2.4 编译器和编译入门 53 2.4.1 定义编译器 54 2.4.2 编译器架构 55 2.4.3 列表文件 58 2.4.4 专用编译器 59 2.5 执行环境 60 2.5.1 软件执行环境（虚拟机） 60 2.5.2 现代处理器的硬件执行环境 63 2.6 结论 68 第3章 Windows基础知识 69 3.1 组件及基本架构 70 3.1.1 简要回顾 70 3.1.2 特征 70 3.1.3 支持的硬件 71 3.2 内存管理 71 3.2.1 虚拟内存和分页 72 3.2.2 工作集 74 3.2.3 内核内存和用户内存 74 3.2.4 内核内存空间 75 3.2.5 区段对象 77 3.2.6 VAD树 78 3.2.7 用户模式的内存分配 78 3.2.8 内存管理API 79 3.3 对象与句柄 80 命名对象 81 3.4 进程与线程 83 3.4.1 进程 84 3.4.2 线程 84 3.4.3 运行状态切换 85 3.4.4 同步对象 86 3.4.5 进程初始化顺序 87 3.5 应用程序编程接口 88 3.5.1 Win32 API 88 3.5.2 本地API 90 3.5.3 系统调用机制 91 3.6 可执行文件格式 93 3.6.1 基本概念 93 3.6.2 映像区段（Image Sections） 95 3.6.3 区段对齐（Section Alignment） 95 3.6.4 动态链接库 96 3.6.5 头部 97 3.6.6 导入与导出 99 3.6.7 目录 99 3.7 输入与输出 103 3.7.1 I/O系统 103 3.7.2 Win32子系统 104 3.8 结构化异常处理 105 3.9 结论 107 第4章 逆向工具 109 4.1 不同的逆向方法 110 4.1.1 离线代码分析 110 4.1.2 现场代码分析 110 4.2 反汇编器——ILDasm 110 4.3 调试器 116 4.3.1 用户模式调试器 118 4.3.2 内核模式调试器 122 4.4 反编译器 129 4.5 系统监控工具 129 4.6 修补工具 131 Hex Workshop 131 4.7 其他类型的逆向工具 133 可执行程序转储工具 133 4.8 结论 138 第2部分 应用逆向 第5章 未公开的技术 141 5.1 逆向和互操作性 142 5.2 基本原则 142 5.3 定位未公开的API函数 143 我们要找什么？ 144 5.4 案例研究：NTDLL.DLL中的 5.4 Generic Table API 145 5.4.1 RtlInitializeGenericTable 146 5.4.2 RtlNumberGenericTableElements 151 5.4.3 RtlIsGenericTableEmpty 152 5.4.4 RtlGetElementGenericTable 153 5.4.5 RtlInsertElementGenericTable 168 5.4.6 RtlLookupElementGenericTable
数据分析.doc
12-23
数据分析 定义：是指用适当的统计分析方法对收集来的大量数据进行分析，将它们加以汇总和理 解并消化，以求最大化地开发数据的功能，发挥数据的作用。数据分析是为了提取有用 信息和形成结论而对数据加以详细研究和概括总结的过程。 目的：把隐藏在一大批看似杂乱无章的数据背后的信息集中和提炼出来，总结出所研究 对象的内在规律，帮助管理者进行判断和决策。 作用：现状分析、原因分析和预测分析 步骤：明确分析目的与框架、数据收集、数据处理、数据分析、数据展现和撰写报告等 6个阶段。 1、明确分析目的与框架 一个分析项目，你的数据对象是谁？分析目的是什么？要解决什么业务问题？目的明确 之后，就可以梳理分析思路整理分析框架。不同的项目对数据的要求，使用的分析手段 是不一样的。所以这些是进行数据分析的方向和前提。 2、数据收集 数据收集是按照确定的数据分析目的和框架内容，有目的的收集、整合相关数据的一个 过程，它是数据分析的一个基础。 3、数据处理 数据处理是指对收集到的数据进行加工、整理，以便开展数据分析，它是数据分析前必 不可少的阶段。这个过程是数据分析整个过程中最占据时间的，也在一定程度上取决于 数据仓库的搭建和数据质量的保证。数据处理主要包括数据清洗、数据转化、数据提取 和数据计算等处理方法。 4、数据分析 数据分析是指通过分析手段、方法和技巧对处理过好的数据进行探索、分析，提取有价 值的信息，从中发现因果关系、内部联系和业务规律。 这个阶段就要涉及到工具和方法的使用。其一要熟悉常规数据分析方法，如方差、回归 、因子、聚类、分类、时间序列等，这些我在学校可以学习。其二是熟悉数据分析工具 ，Excel最常见，还有专业的分析软件，如数据分析工具SPSS/SAS/R/Matlab等，便于进 行一些专业的统计分析、数据建模等。 5、数据展现 一般情况下，数据分析的结果都是通过图、表的方式来呈现，借助数据展现手段，能更 直观的让数据分析师表述想要呈现的信息、观点和建议。 常用的图表包括饼图、折线图、柱形图/条形图、散点图、雷达图等、金字塔图、矩阵图 、漏斗图、帕雷托图等。 6、撰写报告 最后阶段，就是撰写数据分析报告，这是对整个数据分析成果的一个呈现。通过分析报 告，把数据分析的目的、过程、结果及方案完整呈现出来，以供商业目的提供参考。 一份好的数据分析报告，首先需要有一个好的分析框架，并且图文并茂，层次明晰，能 够让阅读者一目了然。另外，数据分析报告需要有明确的结论、建议和解决方案，不仅 仅是找出问题，后者是更重要的，否则称不上好的分析，同时也失去了报告的意义。 数据挖掘（Data Mining） 数据挖掘是知识发现（KDD）的一个关键步骤。一般是指从数据库的海量数据中通过算法 揭示出隐含的、先前未知的并有潜在价值的信息的过程。它是一种决策支持过程，主要 基于人工智能、机器学习、模式识别、统计学、数据库、可视化技术等。 数据挖掘的定义分为技术上的定义和商业定义： 1.技术上的定义及含义 数据挖掘就是从大量的、不完全的、有噪声的、模糊的、随机的实际应用数据中，提 取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程。这个定义 包括好几层含义：数据源必须是真实的、大量的、含噪声的；发现的是用户感兴趣的知 识；发现的知识要可接受、可理解、可运用；并不要求发现放之四海皆准的知识，仅支 持特定的发现问题。 2.商业角度的定义 按企业既定业务目标，对大量的企业数据进行探索和分析，揭示隐藏的、未知的或验 证已知的规律性，并进一步将其模型化的先进有效的方法。 数据挖掘任务有两类： 一：描述性挖掘任务：刻画数据库中数据的一般特性； 二：预测性挖掘任务：在当前数据的基础上进行推断，以进行预测。 数据挖掘常用的方法： 利用数据挖掘进行数据分析常用的方法主要有分类、回归分析、聚类、关联规则、特征 、变化和偏差分析、Web页挖掘等， 它们分别从不同的角度对数据进行挖掘。 1、分类 分类是找出数据库中一组数据对象的共同特点并按照分类模式将其划分为不同的类，其 目的是通过分类模型，将数据库中的数据项映射到某个给定的类别。它可以应用到客户 的分类、客户的属性和特征分析、客户满意度分析、客户的购买趋势预测等，如一个汽 车零售商将客户按照对汽车的喜好划分成不同的类，这样营销人员就可以将新型汽车的 广告手册直接邮寄到有这种喜好的客户手中，从而大大增加了商业机会。 2、回归分析 回归分析方法反映的是事务数据库中属性值在时间上的特征，产生一个将数据项映射到 一个实值预测变量的函数，发现变量或属性间的依赖关系，其主要研究问题包括数据序 列的趋势特征、数据序列的预测以及数据间的相关关系等。它可以应用到市场营销的各 个方面，如客户寻求、保持和预防客户流失活动、产品生命周期分析、销售趋势
会计理论考试题
03-07
第一套 选择题 1.计算机感染病毒后会产生各种现象，以下不属于病毒现象的是__D__。 A、文件占用的空间变大 B、发生异常蜂鸣声 C、屏幕显示异常图形 D、机内的电扇不转 2. Windows98支持下面___C__网络协议。 A、Net BEUI B、IPX/SPX C、TCP/IP D、Banyan VINES 3.为了方便人们记忆；阅读和编程，把机器语言进行符号化，相应的语言称为__D__。 A、数据库系统 B、高级语言 C、源程序 D、汇编语言 4. 应用程序窗口缩成图标后，___A____是不正确的说法。 A、应用程序停止运行 B、应用程序继续运行 C、应用程序图标就放到了任务栏上 D、单击该图标，窗口就还原了 5.窗口右上角的"X"按钮是___C___。 A、最小化 B、最大化 C、关闭 D、选择 6.为了以最佳方式、最少的重复，为多种应用服务，把数据集中起来以一定的组织方式存在计算机的外存储器中，就构成 __D___ 。 A、FoxBASE B、DOS C、数据库管理系统 D、数据库 7.用紧急启动盘(ESD)启动计算机后，屏幕上出现的信息是___B____。 A、Windows98桌面 B、A＞ C、Windows98资源管理器 D、C＞ 8.关于文件的含义，比较正确的说法应该是 ___A____ 。 A、记录在存储介质上的一组相关信息的集合 B、记录在磁盘上的一组相关信息的集合 C、记录在磁盘上的一组相关程序的集合 D、记录在存储介质上的一组相关程序的集合 9.___B___是Windows管理文件的特征，与MS-DOS的目录类似。 A、快捷键 B、文件夹 C、任务条 D、开始菜单 10.CAI是指__C___。 A、计算机辅助设计 B、计算机辅助制造 C、计算机辅助教学 D、计算机辅助管理 11.在资源管理器中删除文件的操作，错误的是选中文件后， ___A____。 A、在“编辑”菜单中选“删除”命令 B、按Delete键 C、单击右键，选“删除”命令 D、在文件菜单中选“删除”命令 12.机器语言是__C___。 A、源程序 B、用符号代替的高级语言 C、CPU能接受的基本指令 D、接近自然语言的计算机指令 13.下列关于计算机病毒的说法中，正确的是 __A___ 。 A、计算机病毒通常是一段可运行的程序 B、反病毒软件可清除所有病毒 C、加装防病毒卡的微机不会感染病毒 D、病毒不会通过网络传染 14.在Windows98中，如果删除了软盘上的文件，则该文件在Windows98中___A____。 A、不可恢复 B、可以在“回收站”中找到 C、可以恢复 D、可以在“我的公文包”中找到 15.下列软件中不属于系统软件的是 ___D__ 。 A、Windows B、Visual FoxPro C、UCDOS D、WPS97 16.应用软件在计算机普及中起重要作用，下列 ___D__ 都属于应用软件。 A、WPS、DOS、Lotusl-2-3 B、WIndows95、Word、Excel C、UNIX、AutoCAD、PoewPoint D、Word、Lotus 1-2-3、AutoCAD 17.编译软件属于 ___C___ 。 A、数据库管理系统 B、工具软件 C、系统软件 D、应用软件 18.计算机病毒最大的危害是__D____。 A、计算机病毒具有传染性 B、计算机病毒会传染给人类 C、计算机病毒具有破坏性 D、计算机病毒具有传染性和破坏性 19.系统软件与应用软件的相互关系是 __D___ 。 A、前者以后者为基础 B、每一类都以另一类为基础 C、每一类都不以另一类为基础 D、后者以前者为基础 20.计算机辅助设计软件主要用于___B___。 A、文字处理 B、制图和设计 C、实时控制 D、科学计算 21.计算机操作系统的作用是 __D___ 。 A、控制计算机的硬件设备 B、执行用户编写的源程序 C、对各种数据进行操作 D、控制和管理系统的软硬件资源 22.在硬盘上找某个文件，但不知在哪个文件夹中，下列___B____方法较快。 A、打开“我的电脑”，选C盘，再按文件夹查找 B、在“开始”菜单中选择“查找”命令 C、在资源管理器的“工具”菜单中单击“查找”命令 D、在写字板的“编辑”菜单中选择“查找”命令 23.如果要把C盘某个文件夹中的一些文件复制到C盘的另外一个文件央中，在选定文件后，若采用拖放操作，可以用___B___目标的方法。 A、直接拖至 B、Ctrl十拖至 C、Alt十拖至 D、单击 24.Windows98中的磁盘的根文件夹是___B___。 A、在“文件”菜单中选择“新建”命令产生 B、格式化磁盘时，系统自动产生 C、在桌面上单击右键，再选择“新建”命令产生 D、在“编辑”菜单中选择“复制”命令产生 25.Windows98对话框的____C____是给用户提供输入信息的。 A、列表框 B、复选框 C、文本框 D、数值框 26.在Windows98中，如果要输入GB2312-80规定以外的汉字，应当____C____。 A、从Windows98的CD盘上安装GBK汉字输入法 B、从软件厂商购买GBK汉字输入法 C、选择全拼输入法来输入汉字 D、在控制面板中选“输入法”，选择CBK汉字输入法 27.要想在文章中输入希腊字母“π”，应___B___。 A、用英文字母“PI”代替B、右击“输入法状态”窗口中的软键盘按钮，然后选择希腊字母键盘 C、用电报码输人法输人 D、在“画笔”中，画出该字，再粘贴到文章中 28.Windows98中的文件系统结构是___C__形状。 A、网状 B、层次 C、树形 D、链状 29.显示卡速度对Windows98的系统性能影响的因素有___A____。 A、Windows98的GUI特点 B、背景图案 C、屏幕保护程序 D、画笔 30.下列计算机设备中，属于输入设备的是__D___。 A、音箱 B、绘图仪 C、打印机 D、扫描仪 31.启动Windows98中文版后，下列中___C___的图标不是常见的图标。 A、我的电脑 B、回收站 C、资源管理器 D、收件箱 32.多媒体电脑是指 __B___ 。 A、专供家庭娱乐用的电脑 B、能处理文字、图形、影像与声音等信息的电脑 C、装有CD—ROM光驱的电脑 D、价格较贵的电脑，是联网的电脑 33.在声音的数字化过程中，采样频率越高，声音的 _A_ 越好。 A、保真度 B、失真度 C、噪音 D、精度 34.对话框常见的组成元素不含___A___。 A、菜单栏 B、复选栏 C、标签 D、滚动条 35.有关Windows屏幕保护程序的说法，正确的是___A____。 A、可以减少屏幕损耗 B、可以节省计算机内存 C、可以保障系统安全 D、可以增加动感 36.记录在存储介质上的一组相关信息的集合称为 __D_ 。 A、程序 B、磁盘 C、软件 D、文件 37.在资源管理器中，双击扩展名为“.TXT”的文件，Windows98会自动打开___B___。 A、写字板 B、记事本 C、画笔 D、剪贴板 38.下列软件中，___C___都属于系统软件。 A、DOS、WPS、Windows B、AutoCAD、Windows NT、Word C、UNIX、DOS、WindoWs D、UNIX、C、MIS 39.在资源管理器中删除硬盘上的文件后，错误的说法是___B____。 A、被删除的文件放到“回收站”中了 B、被删除的文件将无法恢复 C、用户可以从“回收站”中恢复被删除的文件 D、一旦“回收站”被清空，被删除的文件将无法恢复 40.用高级语言编写的源程序，必须经过__B___处理，计算机才能执行。 A、汇编 B、解释或编译 C、解释 D、编译 判断题 1.计算机的常用输入设备有键盘和鼠标器。（ Y ） 2.软盘要远离如电话、录音设备等热源、磁源。（ Y ） 3.硬盘格式化分二个阶段,低级格式化和高级格式化。（ N ） 4.硬盘格式化分三个阶段,其先后顺序为低级格式化、分区、高级格式化。（ Y ） 5.西文工作方式下不可输入汉字。（ Y ） 6.微机的键盘是一种分离式的智能键盘,通过电缆与显示器连接。（ N ） 7.写保护口用于保护存储在软盘片上的信息,避免误写入信息或计算机病毒的侵入。（ Y ） 8.常见的形码汉字输入技术有表形码和五笔字型码。（ N ） 9.汉字语音识别输入技术属于音形码汉字输入技术。（ N ） 10.计算机的常用输出设备有打印机和显示器。（Y ） 11.微机中内存储器指的就是只读存储器(ROM)。（ N ） 12.常见的形码汉字输入技术有全拼码和双拼码。（ N ） 13.微机的键盘是一种分离式的智能键盘,通过电缆与主机连接。（ Y ） 14.计算机的常用输出设备有打印机和键盘。（ N） 15.汉字语音识别输入技术属于汉字智能输入技术。（ Y ） 16.硬盘安装在主机箱内,一般用符号C:表示,称为C盘。（ Y ） 17.供软盘驱动器定位确定所需的读写位置的是索引孔。（ Y ） 18.供软盘驱动器定位确定所需的读写位置的是读写窗口。（ N ） 19.软盘插入软盘驱动器后,驱动器的读写就通过读写窗口存取信息。（ Y ） 20.计算机的常用输入设备有打印机和键盘。（ N ） 第二套 选择题 1.PC机中 Intel8088、80286、80386、80486，PemiumPⅡ、PⅢ是指_D_的不同型号。 A、显示器 B、内存储器 C、外存储器 D、微处理器 2.用高级语言来编写的程序 ___D___ 。 A、称为编译软件 B、经编译后，才称为源程序 C、其运行速度远比机器语言编写的程序要快 D、需要转换成机器语言后，计算机中的CPU才能执行 3.计算机病毒是一种对计算机系统具有破坏性的 ___D___ 。 A、高级语言编译程序 B、生物病毒 C、操作系统 D、计算机程序 4.把高级语言的源程序变为目标程序要经过 ___D__ 。 A、编译 B、编辑 C、汇编 D、解释 5.声音与视频信息在计算机内是以 ___D___ 表示的。 A、模拟信息 B、模拟信息或数字信息 C、数字形式D、二进制形式的数字 6.在Windows98中，要恢复回收站中的文件，只要___B____。 A、双击该文件 B、用鼠标把该文件施出回收站 C、单击该文件 D、A、B、C均可 7.在Windows98刚启动时任务栏上不显示的是___C___。 A、“开始”按钮 B、输入法提示 C、“我的电脑”图标 D、时钟显示 8.在Windows98中，图标不可以代表___D____。 A、程序 B、文件 C、文件夹 D、打印机信息 9.计算机病毒是指__D____。 A、生物病毒 B、细菌 C、被损坏的程序 D、特制的小程序 10.文字处理系统是一种 __C__ 。 A、系统软件 B、管理软件 C、应用软件 D、编辑程序 11.Visual Basic 5.0是一种 __C__ 。 A、自然语言 B、机器语言 C、汇编语言 D、高级语言 12.汇编语言是一种 ___C__ 。 A、机器语言 B、高级语言 C、低级语言 D、目标程序 13.PowerPoint是著名的___A___，可用以制作计算机化的演示材料。 A、简报软件 B、报表软件 C、文字处理软件 D、绘图软件 14.选择“重新启动计算机并切换到MS-DOS方式”，在DOS提示符下键入“VER”，屏幕显示____D____。 A、DOS6.22 B、DOS7.0 C、Windows3.2 D、Windows98 15.计算机病毒主要破坏计算机系统的 ___C__ 。 A、显示器 B、软盘 C、软件资源 D、硬盘 16.___A____是我国公安部开发的一种检测和消除计算机病毒的杀毒软件。 A、Kill B、Scan C、Vsafe D、KV300 17.计算机软件包括____C____。 A、用户程序 B、程序 C、程序及其文档 D、指令 18.假设发现某微机的硬盘C感染上了病毒，现有1张含有清病毒软件的系统盘(软盘)，在下面列出的不同操作方法中，较为有效的清除病毒的方法是 ___C___。 A、不关机直接运行软盘中的清病毒软件 B、用硬盘重新自举后运行软盘中的清病毒软件 C、用含有清病毒软件的系统盘重新自举后，再运行软盘中的清病毒软件 D、A．B．C均可 19.下列软件中，不属于应用软件的是 ___D___ 。 A、字表处理软件 B、财务管理软件 C、股市分析软件D、高级语言编译程序 20.磁盘扫描程序(scandisk)可以检测和修复多种逻辑和物理错误，包括__C___。 A、文件名错误 B、磁盘扇区错误 C、文件交叉链接错误 D、文件目录错误 21.从软件归类来看，DOS属于 __A_ 。 A、系统软件 B、应用软件 C、字表处理软件 D、数据库管理系统 22.要把分别用“记事本”、“写字板”和“画笔”建立的三个文件拼接成一个文件，该文件应放在___D___中。 A、记事本 B、写字板 C、画笔 D、资源管理器 23.Windows98的“编辑”菜单中的“粘贴”功能有时是灰色的，只有当__A___，该功能才可使用。 A、剪贴板中有内容 B、选中对象 C、按鼠标右键 D、按鼠标左键 24.Windows98的很多窗口中都有“编辑”菜单，该菜单中的“剪切”和“复制”功能有时是灰色的，只有当___B____后，这两个功能才可使用。 A、剪贴板中有内容 B、选中对象 C、按鼠标右键 D、按鼠标左键 25.Windows98的____A___可以跟踪、监视系统性能。 A、注册表编辑器 B、用户外观文件 C、系统策略编辑器 D、系统监视器 26.有关计算机病毒的传播途径，不正确的说法是 ___D___ 。 A、共用软盘 B、软盘复制 C、借用他人的软盘 D、和带毒盘放在一起 27.Windows98的“帮助”信息是一种___B____技术。 A、文字处理 B、超文本 C、网络 D、联想 28.在Windows98中，32位应用程序理论上能使用的内存最大容量为___C____。 A、2GB B、32MB C、4GB D、2TB 29.计算机病毒的特点 ___A___ 。 A、传播性、潜伏性、破坏性 B、传播性、破坏性、易读性 C、潜伏性、破坏性、易读性 D、传播性、潜伏性、安全性 30.计算机病毒主要造成 ___D__ 。 A、磁盘损坏 B、计算机用户的伤害 C、CPU的损坏 D、程序和数据的损坏 31.在Windows98中，应用程序窗口标题栏最右方的是__C__。 A、最小化 B、最大化 C、关闭 D、还原 32.中文Word是一种___B____。 A、电子表格软件 B、文字处理软件 C、绘图软件 D、网络通信软件 33.系统软件中最重要的是___D___。 A、数据库管理系统 B、诊断程序 C、语言处理程序 D、操作系统 34.某单位的财务管理软件属于 ___B__ 。 A、工具软件 B、应用软件 C、系统软件 D、字表处理软件 35.计算机感染病毒的可能途径是___B___。 A、从键盘上输入数据 B、运行未经审查的软件 C、软盘表面不洁 D、电源不稳 36.多媒体应用必须解决大容量存储器问题，采用__C_是一个较好的解决方案。 A、大容量硬盘 B、大容量软盘 C、CD光盘 D、大容量磁带 37.对计算机用户来讲，最容易接受的是___D____。 A、机器语言 B、汇编语言 C、低级语言 D、高级语言 38.下列软件中，不属于系统软件的是 ___D___ 。 A、操作系统 B、诊断程序 C、编译程序 D、用高级语言编写的程序 39.构成机器语言的是 __B__ 。 A、ASCII码 B、二进制编码 C、十进制编码 D、汉字国际码 40.AutoCAD是一种_____C____。 A、电子表格软件 B、文字处理软件 C、绘图软件 D、网络通信软件 判断题 1.显示器有单色显示器和彩色显示器二种。（ Y ） 2、1个英文字母占1个字节,1个汉字占2个字节。（ Y ） 3.软件在社会信息化和人类文化的发展中具有重要作用。（ Y ） 4.我们把计算机向使用者传递处理结果的设备称为输出设备。（ Y ） 5.只有显示器提供的分辨率大于或等于显示卡提供的屏幕分辨率时,才认为是显示器与显示卡配合正确。（ Y ） 6.一个良好的操作姿势可以使操作员舒适而持久地工作,同时也有利于按键的准确性和快速性。（ Y ） 7.显示器正常工作的前提是要求显示器与显示卡配合正确。（ Y ） 8.Num Lock是带指示灯的数字锁定键,当指示灯亮时,表示光标键有效,数字键无效（ N ） 9.字母的大小写状态由Caps Lock键控制,这是一个带指示灯的锁定键。指示灯亮表示字母为小写状态。（ Y ） 10.为了便于了解程序所需的说明性资料就是文档。（ Y ） 11.显示器是一种重要的人机交互设备,使用计算机离不开使用显示器。（ Y ） 12.操作键盘的要领是:眼睛看显示器,手指管键盘,大脑统指挥,各行其职,通力合作。（ Y ） 13.软件是用户与硬件之间的接口界面。（ Y ） 14.发展计算机科学技术,软件和硬件是不可缺少的两个重要方面。（ Y ） 15.鼠标器是一种输入设备,主要用于光标定位或完成某种特定的输入。（ Y ） 16.程序是对所要解决问题的各个对象和处理过程的描述。（ Y ） 17.全拼拼音输入法要求通过西文键盘逐个字母输入汉字的拼音,再从提示行所显示的同音字中选取所需要的汉字。（ Y ） 18.常见的音码汉字输入技术有全拼码和智能ABC码。（ Y ） 19.点阵打印机是通过针状打印头在电磁铁吸合驱动下,通过对色带撞击,在打印纸上留下字符。（ Y ） 20.Num Lock是带指示灯的数字锁定键,当指示灯亮时,表示数字键有效,光标键无效（ Y ） 第三套 选择题 1.某用户在word中建立了一个文档，并用文件名new word document存盘，在DOS提示符下，该文件名将转变为____C____。 A、newword.doc B、newwor~1.txt C、newwor~1.doc D、什么也没有 2.目前Pentium机的CPU能够同时处理的二进制数据的位数是___C___。 A、16 B、24 C、32 D、64 3.计算机系统中包含了多种存储器，其中 __D__ 是外存储器。 A、寄存器 B、ROM C、RAM D、磁盘 4.Windows98是一种___C__操作系统。 A、单用户单任务 B、多用户单任务 C、抢占式多任务 D、非抢占式多任务 5.___A___是直接运行在裸机上的最基本的系统软件，它负责对各类资源进行统一控制、管理、调度和监督。 A、操作系统 B、语言处理程序 C、数据库管理系统 D、工具软件 6.在“我的电脑”中，用鼠标__C___图标的方法，可打开一个文件或文件夹。 A、单击 B、Ctrl+单击 C、双击 D、右击 7.利用键盘，按__B___可以实行中西文输入方式的切换。 A、Alt+空格键 B、Ctrl+空格键 C、Alt+Esc D、Shift+空格键 8.窗口与对话框在外观上的最大区别在于____A___。 A、是否有菜单栏 B、是否具有标签 C、是否具有“×” D、选择的项目是否很多 9.汇编语言源程序经 ___D___汇编得到机器指令形式的目标代码。 A、C编译程序 B、FORTRAN编译程序 C、PASCAL编译程序 D、汇编程序 10.选择Windows窗口菜单命令一般____C___选项。 A、用鼠标右键单击 B、用鼠标右键双击 C、用鼠标左链单击 D、用鼠标左键双击 11.计算机硬件唯一能直接理解的语言是 ___A___ 。 A、机器语言 B、汇编语言 C、C语言 D、FORTRAN语言 12.防病毒卡能 ___D__ 。 A、自动发现并阻止任何病毒的入侵 B、自动清除已感染的所有病毒 C、杜绝病毒对计算机的侵害 D、自动发现大部分病毒的入侵并及时阻止或提醒用户 13.微机硬件系统中地址总线的宽度对__B___影响最大。 A、存储器的访问速度 B、可访问存储器的空间大小 C、存储器的字长 D、存储器的稳定性 14.在资源管理器中，要选择连续的多个文件，应____C____。 A、连续单击要选择的对象 B、先单击第一个对象，按住[Ctrl]键，再单击最后一个对象 C、先单击第一个对象，按住[Shift]键，再单击最后一个对象 D、按住[Ctrl]键，先单击第一个对象，再单击最后一个对象 15.计算机的内存储器是指___C____。 A、RAM和寄存器 B、RAM和磁盘 C、RAM和ROM D、ROM和磁盘 16.现在使用的计算机，其工作原理是 ___C___ 。 A、自动操作 B、逻辑判断 C、存储程序和程序控制 D、识别控制代码 17.系统总线上的信号，有 ___D___ 。 A、地址信号 B、数据信号、控制信号 C、控制信号 D、数据信号、控制信号、地址信号 18.外存中的数据与指令必须先读入___C___，然后计算机才能进行处理。 A、CPU B、ROM C、RAM D、Cache 19.下列关于存储器的叙述中，正确的是 __C___ 。 A、外存储器能与CPU直接交换数据 B、衡量主存储器的主要技术指标是字长 C、外存储器能与主存储器成批交换数据 D、内存储器不能与CPU直接交换数据 20.在Windows98中文版中，___D___不是合法的文件名形式。 A、My.system.two.txt B、昨天 今天 明天.DOC C、AAA D、A>B.EXE 21.计算机病毒的特点有以下几种描述，其中 ___B____是不正确的。 A、破坏性 B、偶然性 C、传染性 D、潜伏性 22.关于“窗口”与“对话框”在外观上区别，以下说法不正确的是__B____。 A、窗口可以改变尺寸 B、对话框不能改变尺寸，窗口与对话框都具有“最小化”按钮 C、窗口与对话框都具有“×”按钮 D、窗口与对话框都具有选择项目 23.窗口常见的组成元素有__D____。 A、对话框 B、复选栏 C、标签 D、菜单栏、滚动条 24.在Windows98中的窗口有___D____。 A、文档窗口 B、应用程序窗口 C、对话框 D、A或B 25.21世纪的计算机将向巨型化、多媒体及 __D___ 方向发展。 A、微型化 B、智能化 C、网络化 D、微型化、智能化、网络化 26.要在桌面上改变快捷键的图标，应___B___。 A、把新图标拖到快捷键上 B、右击快捷键，单击“属性”，然后选择“改变图标” C、在“资源管理器”中，选择“编辑”，然后选择“选项” D、删除快捷键，然后建一个新的快捷键图标 27.下列有关Windows剪贴板的说法，正确的是___A____。 A、剪贴板是一个在程序或窗口之间传递信息的临时存储区 B、没有剪贴板查看程序，剪贴板不能工作 C、剪贴板内容不能保留 D、剪贴板每次可以存储多个信息 28.FoxBase是一种 ___C___数据库管理系统。 A、层次型 B、网状型 C、关系型 D、树型 29.FORTRAN语言主要应用在 ___A___ 中。 A、科学计算 B、信息处理 C、实时控制 D、计算机和辅助设计 30.下面__A__组设备包括：输入设备、输出设备和存储设备。 A、鼠标器、绘图仪、光盘 B、磁盘、鼠标器、键盘 C、CRT、CPU、ROM D、磁带、打印机、激光打印机 31.要把当前窗口的信息复制到剪贴板上，应按___B___。 A、Prt Scr B、Alt+Prt Scr C、“粘贴”按钮 D、“复制”按钮 32.计算机的运算精度通常取决于 ___C__ 。 A、计算机的内存容量 B、计算机的硬盘容量 C、计算机的字长 D、计算机的程序 33.Excel是一种____A___。 A、电子表格软件 B、文字处理软件 C、绘图软件 D、网络通信软件 34.计算机软件可以被粗略地分成两类，即 ____B____ 。 A、系统软件和文字处理软件 B、应用软件和系统软件 C、绘图软件和文字处理软件 D、绘图软件和系统软件 35.高级语言采用解释方式时的执行速度与采用编译方式时的执行速度相比，下列__A__是正确的。 A、相等 B、前者快 C、前者慢 D、不能确定 36.CD—ROM光盘在CD—ROM驱动器上___C___。 A、能读能写 B、只能写入 C、只能读出 D、不能写入但能修改 37.Windows管理内存的能力与MS—DOS相比较，下列__C___是正确的。 A、相等 B、后者大 C、前者大 D、不能确定 38.CD—ROM是 ___C__ 。 A、CD写入器 B、CD刻录机 C、只读光盘 D、换盘机 39.UNIX操作系统于___B___年代在美国电话与电报公司的贝尔实验室中诞生。 A、60 B、70 C、80 D、90 40.微机主要性能指标是 ____C___ 。 A、字长、内存、外设配置、软件配置 B、主频、内存、外设配置、软件配置 C、主频、字长、内存、外设配置、软件配置 D、字长、内存、外设配置、磁盘、软件配置 判断题 1.同一磁盘目录下的文件可以同名。（ N ） 2.高位置1的国标码就是机内码。（ Y ） 3.应用软件一般都是通过系统软件发挥作用。（ Y ） 4.计算机系统中,文件可以是用户自己写的文章或一段程序。（ Y ） 5.应用软件是为特定应用领域专门设计的软件。（ Y ） 6.通配符*只能代替文件名中任意的一个字符。（ N） 7.同一目录下的文件不能同名,但同一目录下的子目录可以同名。（ N ） 8.计算机在运行过程中发生故障,无法正常运行时,通常采用热启动的处理措施。（ Y ） 9.目前,大、中、小型计算机使用的操作系统均为DOS(磁盘操作系统)。（ N ） 10.同一磁盘目录下的文件不能取相同的名字,因为操作系统依靠文件名来管理文件。（ Y ） 11.计算机总线分为三类:地址总线、数据总线和控制总线。它们构成了计算机内部各功能器件的信息通路。（ Y ） 12.通配符*可以代替文件名中任意多个任意字符。（ Y ） 13.通配符?可以代替文件名中一个任意字符。（ Y ） 14.给文件命名时,文件名是不可缺少的,而扩展名可有可无。（ Y ） 15.同时按下Ctrl、Alt、Del三键,可以冷启动。（ Y ） 16.给文件命名时,不仅要有文件名,扩展名也是必不可少的。（ N ） 17.DOS是英文Disk Operating System(磁盘操作系统)的首字缩写。（ Y ） 18.操作系统是一种应用软件,由一组计算机程序组成。（ N ） 19.操作系统是一种系统软件,它统一管理计算机的所有硬件资源和软件资源。（ Y ） 20.文件名中可用的字符为英文字母A-Z及0-9的数字,其他字符均为不合法字符。（ N ） 第四套 选择题 1.Windows98中用于引导用户完成大多数日常操作的菜单在__C___菜单中。 A、资源管理器 B、word C、“开始” D、我的电脑 2.内存中的随机存储器通常是用___A__来表示的。 A、RAM B、EPROM C、Cache D、ROM 3.以下 ___C___ 的说法不正确。 A、软件与硬件一样也是一种商品 B、未经软件著作权人同意，复制其软件的行为是侵权行为 C、复制加密过的软件是违法行为，但不加密的软件不受法律保护 D、我国的软件著作权受《中华人民共和国著作权法》的保护 4.CPU每执行一条 ___B___ ，就完成一个最基本的算术逻辑运算或数据的存取操作。 A、命令行 B、指令 C、程序 D、语句 5.一般来说，Pentium/200／32M微机中的“200”含义是__B____。 A、总线为200位 B、主频为200MHz C、硬盘容量为200M D、字长为200位 6.Windows98中，下列启动帮助系统的方法中，不正确的是___D___。 A、选择“帮助”菜单，然后选择“帮助主题” B、按[F1]功能键 C、单击“开始”按钮，然后单击“帮助” D、选择窗口右上角的“帮助”按钮 7.在Windows98系统中，“帮助”文件一般采用___A__结构。 A、超文本 B、ASCII文本 C、Word中的DOC文本 D、网络 8.以下说法正确的是____A___。 A、用户可以自己定制“开始”菜单、“程序”菜单以及“启动”菜单 B、被放入回收站内的文件不可以被还原 C、用户可以利用“控制面板”中的“字体”来设置汉字输入法特性 D、利用“网上邻居”可以浏览网上其他计算机的所有资源 9.计算机的常用输出设备有____A___ 。 A、显示器、打印机、绘图仪 B、打印机、显示器、鼠标器 C、显示器、ROM、RAM D、键盘、显示器、打印机 10.要实现Windows98的拨号网络功能，应安装___D____。 A、CD-ROM B、声卡解压卡 C、网卡 D、调制解调器 11.计算机的存储体系一般指___C___。 A、驱动器和磁(光)盘片 B、RAM和ROM C、内存和外存 D、硬盘和软盘 12.Windows属于一种__A_方式操作系统。 A、多任务图形 B、单任务图形 C、多任务字符 D、单任务字符 13.Windows98支持____D___的共享，并且具有很好的网络安全性。 A、打印机 B、CD-ROM、传真、调制解调器等设备 C、文件和文件夹 D、三种都是 14.Windows98是___D___软件。 A、数据库管理系统 B、语言处理程序 C、实用程序与工具 D、操作系统 15.有关软盘的描述，___C___是错误的。 A、1.44MB的3.5英寸软盘每面有80磁道，每道18扇区 B、软盘有一系列同心圆周，一个圆周称为1个磁道 C、软盘最里圈的磁道为0磁道 D、每个磁道分为若干个段，每个段称为1个扇区 16.在计算机中要编辑一个已有的磁盘文件，则必须将文件读至_D__。 A、运算器 B、控制器 C、CPU D、内存储器 17.微机中的I／O接口卡位于____A___之间。 A、CPU与外设 B、主存与外存 C、总线与外设 D、输入设备与输出设备 18.下列设备中，属于输出设备的是___D__。 A、扫描仪 B、鼠标器 C、键盘 D、音箱 19.一般来说，机器指令由___D__组成。 A、ASCII码和BCD码 B、地址码和区位码 C、区位码和操作码 D、操作码和地址码 20.下列关于文件和文件夹的说法中，错误的是__C____。 A、在一个文件夹下，可包含一个与之同名的文件夹 B、在一个文件夹下，不能存在两个同名的文件夹 C、文件下不能包含文件夹，但能包含其他文件 D、文件夹下可包含文件和文件夹 21.在3．5英寸的软盘上，有一带活动滑块方形小孔，它的作用是___A___。 A、写保护 B、读保护 C、驱动器孔轴 D、读写保护 22.要将整个屏幕内容复制到剪贴板上，应按__C____。 A、“剪切”按钮 B、“粘贴”按钮 C、[Prt Scr]键 D、“拷贝”按钮 23.计算机中用于连接CPU、内存、I／O设备等部件的设备是__B__。 A、地址线 B、总线 C、控制线 D、数据线 24.以下属于应用软件而不属于通用应用软件的是 ___D__ 。 A、网络与通信软件 B、文字处理软件 C、统计软件 D、民航售票管理信息系统 25.应用软件是___A____ 。 A、用于各领域的专用软件 B、用来编辑源程序的软件 C、用于PC微机上的操作系统 D、PC微机上的数据库管理系统 26.计算机软件受到___B___保护。 A、专利法和教育法 B、专利法和著作权法 C、教育法和著作权法 D、软件保护条例和教育法 27.一般磁盘的磁道是同心圆，而CD—ROM光盘上记录信息的光道是__B____。 A、等高线 B、螺旋线 C、电缆线 D、双绞线 28.目前常用的多用户操作系统为 ___A___ 。 A、UNIX B、DOS C、Windows NT D、UNIX和Windows NT 29.计算机系统是指 ___C___ 。 A、计算机硬件 B、数据库系统和操作系统 C、硬件和软件系统 D、计算机软件 30.计算机外部设备包括 ___C__ 。 A、键盘、光盘和RAM B、ROM、硬盘和显示器 C、打印机、鼠标器和辅助存储器 D、主存储器、硬盘和显示器 31.计算机的硬件由 ___A___ 五部分组成。 A、CPU、总线、主存、辅存和I／O设备 B、CPU、主存、辅存、键盘和I／O设备 C、CPU、总线、主存、打印机和I／0设备 D、CPU、运算器、主存、总线和I／O设备 32.视屏卡主要是用来支持___C___ 。 A、视屏信息的输入 B、视屏信息的输出 C、视屏信息的输入和输出 D、视屏信息的传输 33.一般来说，Pentium/200/32M微机中的32M的含义是___A___。 A、内存为32MB B、软盘为32MB C、型号为32M D、总线字长为32M 34.下列计算机设备中，___C___不是输入设备。 A、扫描仪 B、键盘 C、绘图仪 D、鼠标 35.PentiumⅢ微处理器运算速度快的原因是___D___ 。 A、采用了流水线技术 B、提高了时钟频率 C、优化了指令执行时间 D、三者都是 36.在表示存储器的容量时，如果用1MB作为单位，其准确的含义是__D___。 A、1024B B、1024TB C、1024GB D、1024KB 37.在一台PC机中，最关键的物理部件是___B__。 A、显示器 B、系统板 C、键盘 D、打印机 38.硬盘的容量比软盘大得多，其读写速度比软盘___C____。 A、慢得多 B、差不多 C、快得多 D、不能确定 39.SVGA、EGA、VGA标志着 __D__ 的不同规格和性能。 A、硬盘 B、打印机 C、存储器 D、显示器 40.Windows98的任务栏不可以____A___。 A、和桌面图标一样删除 B、隐藏 C、改变大小 D、移动 判断题 1、磁盘读写时间比平时长,可用的存贮空间突然变小,这些有可能是计算机病毒造成的。Y 2、当你用一张带引导型病毒的系统盘启动计算机时,病毒就随之进入内存,感染硬盘。Y 3、计算机病毒是一种微生物病毒,会通过计算机传播给人类。N 4、硬盘带引导型病毒,当用硬盘启动系统时,病毒就也启动起来进入内存。Y 5、硬盘带引导型病毒,当用硬盘启动系统时,DOS可以正确启动,而不受病毒的危害。N 6、操作文件更快捷的方法是双击要操作的文件，会弹出一个快捷菜单。N 7、贴有写保护的软盘片,在带毒的计算机上运行时,不会染上病毒。Y 8、计算机的硬件系统由运算器、控制器、存储器、输入设备和输出设备五大部件组成。Y 9、文件型病毒主要传染可执行文件,当执行该文件时,病毒首先进入内存,控制系统,伺机进行传播和破坏活动。Y 10、计算机病毒不会造成机器的死机。N 11、所谓恶性病毒,即该病毒发作时将破坏数据,删除文件,使系统瘫痪,但其不占用CPU资源。N 12、病毒会入侵一台单个的计算机系统,而将计算机连网后,就不会再受病毒的侵扰了。N 13、计算机五大部件相互间传递信号由总线来完成。根据信号类型的不同,总线分为二类:地址总线和数据总线。N 14、当你用一张带引导型病毒的系统盘启动计算机时,病毒会进入内存,但不会感染硬盘。N 15、无论是单机系统,还是网络系统,都会受到病毒的侵扰。Y 16、内存突然变小,以前能运行的程序突然不能运行。这种情况表示计算机可能带病毒。Y 17、引导型病毒是在系统引导时就进入内存,从而控制系统,进行传播和破坏活动。Y 18、所谓恶性病毒,即该病毒发作时将破坏数据,删除文件或使整个系统处于瘫痪状态等。Y 19、所谓良性病毒,只占用系统CPU资源和干扰系统工作,并不破坏数据。Y 20、程序装入时间比平时长,程序运行比平时慢,出现这种情况,表示计算机可能有病毒Y 第五套 选择题 1.资源管理器不能管理与访问的计算机资源是__D___。 A、A盘、C盘、打印机、绘图仪 B、桌面上的各种图标 C、连在网络上的计算机 D、连在网络上其他计算机内的显示卡 2.通常下列设备中不能作为输入设备的是 ___B___ 。 A、鼠标 B、显示器 C、键盘 D、扫描仪 3.若要把C盘上的某个文件复制到A盘，选定文件后，最简捷的操作是___A___。 A、将其直接施放到A盘图标 B、按住[Alt]后，将其施放到A盘图标 C、按住[Esc]后，将其施放到A盘图标 D、按住[Shift]后，将其施放到A盘图标 4.下列描述中，正确的是 ___C____ 。 A、激光打印机是击打式打印机 B、软盘驱动器是存储器 C、微机运算速度可用每秒执行指令的条数来表示 D、显示器的显示质量与适配器无关 5.下列设备中，属于计算机输入设备的是___B____。 A、绘图仪 B、扫描仪 C、显示器 D、打印机 6.新软盘使用之前必须__C___。 A、装入引导程序 B、装入DOS C、格式化 D、写保护 7.Windows操作具有__B___的特点。 A、首先选择操作项，然后再选择操作对象 B、首先选择操作对象，然后再选择操作项 C、需将操作对象拖到操作项上 D、需同时操作对象和操作项 8.在计算机中程序主要存放在__B___中。 A、键盘 B、存储器 C、微处理器 D、显示器 9.显示器是计算机的____B___。 A、微处理器 B、输出设备 C、输入设备 D、存储器 10.Windows98的“应用程序窗口”与“文档窗口”，它们存在的关系是__B___。 A、文档窗口打开之后，应用程序窗口才能打开 B、应用程序窗口打开之后，文档窗口才能打开 C、一个文档窗口内，可以打开多个应用程序窗口 D、应用程序窗口中只能打开一个文档窗口 11.3.5英寸高密度软磁盘的容量一般为 ____A__ 。 A、1.44MB B、1MB C、1.2MB D、360KB 12.目前使用的光盘存储器CD-ROM是___A__。 A、只读型 B、一次写入型 C、可抹型 D、读写型 13.在资源管理器中，双击扩展名为“.BMP"的文件，Windows98会自动打开__B__应用程序窗口。 A、写字板 B、画笔 C、记事本 D、剪贴板 14.在菜单命令中，后面跟有__A___，执行时就会有对话框。 A、… B、√ C、• D、? 15.下列关于Windows98的叙述中，不正确的是__C____。 A、Windows98是一个32位、多任务、图形方式的操作系统 B、Windows98的运行无需DOS支持 C、大部分DOS软件不能在Windows98下运行 D、Windows98支持长达255个字节的文件名 16.Windows98提供了各种系统工具来帮助用户管理系统，其中___A__可以检查、诊断和修复各种类型的磁盘损坏和错误。 A、磁盘扫描程序 B、磁盘空间管理 C、磁盘碎片整理程序 D、备份程序 17.打印机属于__B___。 A、输入设备 B、输出设备 C、运算器 D、控制器 18.二进制加法10010100十110010的和为___A___。 A、11000110 B、10100110 C、10110110 D、11100110 19.在微机中，软盘连同其驱动器属于__A____。 A、外存储器 B、输入设备 C、输出设备 D、内存 20.在中文Windows98中，文件名或文件夹____C____。 A、 最多不能超过8个字符 B、可以用任意多个字符 C、不超过255个ASCII字符 D、不可以使用汉字 21.下列设备中不能作为输出设备的是___A___。 A、键盘 B、打印机 C、显示器 D、绘图仪 22.有组织地、动态地存储大量数据，且能高效地使用这些数据的系统是__C___。 A、辅助设计软件 B、应用软件 C、数据库管理系统 D、编译软件 23.以下 ___B__ 中的两个软件都是系统软件。 A、UNIX和 MIS B、Windows和 UNIX C、Windows和 MIS D、WPS和 UNIX 24.CPU的主要功能是___C____。 A、传送信息 B、把数据存入存储器 C、识别指令和执行指令 D、控制输入／输出设备 25.内存中有一小部分用于永久存放专用的数据和程序，CPU对它们只取不存，这一部分称为只读存储器，简称__B___。 A、WPS B、ROM C、DOS D、RAM 26.在Windows98中，选择“重新启动计算机并切换到MS-DOS方式”，使用完MS-DOS方式后，键入___C___命令即可返回到Windows98。 A、DOS B、CAI C、EXIT D、EXEC 27.在计算机性能评测技术中，能相对客观评估系统性能，更接近系统实际运行状况的评估方法是___D__ 。 A、使用icomp指数标准 B、使用Benchmark(基准程序测试)方法 C、使用Qaplus、Norton工具 D、测试CPU、磁盘I／O、显示卡I／O总性能 28.软盘若进行写保护，则___C___。 A、文件能存入，也能取出 B、文件能存入，但不能取出 C、文件不能存入，但能取出 D、文件不能存入，也不能取出 29.一台完整的计算机硬件由 ___D___ 构成。 A、中央处理器、输入设备、输出设备 B、运算器、存储器、输入设备、输出设备 C、CPU、RAM、ROM、总线 D、中央处理器、存储器、输入设备、输出设备 30.软盘驱动器的读写磁头是通过软盘的___D__进行读写信息的。 A、写保护口 B、电子线路 C、护套 D、读写窗口 31.计算机中系统软件一般指 ___C___ 。 A、用于处理大量数据的软件 B、用于输入、存储、编辑文字材料的软件 C、由一系列完成基础工作的指令形成的专门软件 D、专门为某一应用而编制的软件 32.微机中常用的输入设备是 __A___ 。 A、键盘 B、软盘 C、硬盘 D、显示器 33.鼠标器是一种 ___B__ 。 A、输出设备 B、输入设备 C、运算器 D、控制器 34.键盘上的数字、英文字母、标点符号、空格等键，称为__A__。 A、字符键 B、控制键 C、功能键 D、运算键 35.速度快，印字质量好，噪音低，但价格昂贵的打印机是___A____打印机。 A、激光 B、喷墨 C、针式 D、点阵式 36.CGA、VGA、EGA的含义是___D___。 A、微机型号 B、打印机型号 C、显示标准 D、显示器型号 37.80486是32位处理器，“32"指____B___的技术指标。 A、速度 B、字长 C、容量 D、二进制位 38.在微机中，I／O的中文意思是__C__。 A、读写存储器 B、操作系统 C、输入／输出 D、接口电路 39.3．5英寸的软盘，当写保护窗口透光时___C___。 A、只能写不能读 B、既可读又可写 C、只能读不能写 D、不起任何作用 40.关于剪贴板的操作，以下描述正确的是____C____。 A、剪贴板只保留最近一次做“剪切”操作的内容，做两次以上“粘贴”操作后，剪贴板里的信息便丢失 B、剪贴板可保留多次做“剪切”操作的内容，做多次“粘贴”操作后信息仍然保留 C、剪贴板只保留最近一次做"剪切"操作的内容，做多次"粘贴"操作后，剪贴板信息也不会丢失 D、剪贴板是各个应用程序之间传输信息的缓冲区，做多次"粘贴"操作后或者退出Win98之后，剪贴板信息仍然保留 判断题 1.超大规模集成电路的发展使计算机日趋微型化。（ Y ） 2.国标码中收录的一级汉字有3755个,按部首排序（ N ） 3.国标码中收录的一级汉字有3755个,按拼音顺序排序。（ Y ） 4.软盘染上病毒后,进行FORMAT格式化处理,可以消除软盘上的病毒。（ Y ） 5.所谓国标码就是拼音码。（ N ） 6.软盘染上病毒后,进行FORMAT格式化处理,不能消除软盘上的病毒。（ N ） 7.国标码中收录的二级汉字有3008个,按部首排序。（ Y ） 8.为了减少系统运行环境中引导型病毒的侵入,最好用硬盘启动系统。（ N ） 9.防病毒卡是一块插件板,插于计算机内的扩展槽中。它是一种依靠硬件来捕捉病毒,而无须软件配合的防毒技术。（ N ） 10.计算机是高科技的产物。它无所不能,因此人们不必编制程序,计算机也会按人的要求工作。（ N ） 11.Windows中的图标是代表程序、文件、文件夹等各种对象的小图像。（ Y ） 12.计算机病毒防范首先必须以预防为主,即保护传染对象不受病毒的传染。（ N ） 13.所谓国标码就是1981年由国家标准局公布的《信息交换用汉字编码字符集》(GB2312-80)。（ Y ） 14.在“记事本”中保存文档时，如果用户没有指定扩展名，系统将给文件加上扩展名“.TXT"。（ Y ） 15.所谓国标码就是五笔字型码。（ N ） 16.人们通过编制程序来控制计算机,程度设计语言是编制程序时的语法规则。（ Y ） 17.当NumLock批示灯亮时只能输入大写字母。（ N ） 18.计算机的分类指标只依据该计算机的内存和CPU的速度等硬件信息.（ N ） 19.拖动Windows应用程序窗口的标题栏可以在桌面上移动窗口。（ Y ） 20.计算机病毒防范可以从三个方面来进行即:预防、检查和消毒。（ Y ） 第六套 选择题 1.常用工具栏中有一个下拉列表，其作用是___D___。 A、拼写检查 B、显示字体 C、显示字号 D、显示比例 2.下列关于计算机基础知识的叙述中，正确的是___D___。 A、32位微机的字长为两个字节 B、字长是标志计算机运行速度的一项技术指标 C、32MB=32000000B D、计算机系统由硬件和软件两部分组成 3.在微机中，80486通常是指___D___。 A、微机名称 B、主频速度代号 C、存储容量代号 D、微处理器型号 4.在微机中，微处理器的主要功能是进行___D____。 A、算术运算 B、逻辑运算 C、算术及逻辑运算 D、运算及控制 5.在计算机中，RAM指___B___。 A、只读存储器 B、随机存储器 C、内存储器 D、外存储器 6.在微机中存取速度最快的存储器是___C__。 A、硬盘 B、软盘 C、内存 D、光盘 7.内存与光盘相比，主要差别是____A___。 A、存取速度快、容量小 B、存取速度快、容量大 C、存取速度慢、容量大 D、存取速度慢、容量小 8.ROM与RAM的主要不同之处在于____C___不同。 A、存储速度 B、存储介质 C、存储性质 D、存储容量 9.ROM中存储的数据在断电后___B___。 A、部分丢失 B、不会丢失 C、不一定丢失 D、完全丢失 10.鼠标指针指向某个工具栏上的一个按钮时，显示按钮名称的黄色矩形是__C__。 A、标记 B、菜单 C、工具提示信息 D、帮助信息 11.计算机的存储系统一般指___C___。 A、RAM和BOM B、硬盘和软盘 C、内存和外存 D、驱动器和磁(光)盘片 12.双击段落左边的选定栏，则选定了___C____。 A、一行 B、一个字 C、一段 D、一页 13.要选定表格中的一列，可以___A____。 A、在出现向下黑色箭头时，单击左键 B、在出现左箭头光标时，单击左键 C、在"表格"菜单中，按"选定列"子项 D、在出现右箭头光标时，单击左键 14.TrueType字体的主要优点是___C_____。 A、具有艺术字体 B、在屏幕和打印机上具有相同的效果 C、可以无级缩放 D、可以设置成粗体或斜体 15.要使文档中每段的首行自动缩进2个汉字，在选定段落后，可以使用标尺上的___C___。 A、左缩进标记 B、右缩进标记 C、首行缩进标记 D、悬挂缩进标记 16.Word中模式匹配查找中能使用的通配符是__D__。 A、+和- B、/和* C、?和/ D、*和? 17.在Word中，___A____ 实际上对文档的编辑、排版和打印等操作都将产生影响。 A、页面设置 B、字体设置 C、打印预览 D、页码设置 18.对于一张已填制好数据的表格，下列说法中正确的是___D___。 A、若合并两个单元格，则这两个单元格中的数据将被删除 B、若拆分一个单元格，则该单元格中的数据将被删除 C、表格的格式将无法再改变 D、表格中的数据颜色可各不相同 19.用户想要通过页面格式来建立一个商业信函、传真等种类的文档，则可__A___。 A、用"文件"菜单中的"新建"命令，选择相应的模板 B、用"插入"菜单，插入相应模板 C、用"工具"栏上的"新建"按钮，选择相应模板 D、用"编辑"菜单，选择相应的模板 20.把计算机中的数据录入到磁盘上，称为___C___。 A、输入 B、读盘 C、写盘 D、输出 21.连接计算机各部件的一组公共通信线称为总线，它由___D__组成。 A、地址总线和数据总线 B、地址总线和控制总线 C、控制总线和数据总线 D、控制总线、地址总线和数据总线 22.计算机和其他一切计算工具最本质的区别是____D____。 A、能自动运行 B、存储容量大 C、高精度和高速度 D、具有逻辑判断功能 23.新一代计算机最突出的特点是__B___。 A、采用大规模集成电路 B、具有智能 C、具有超高速 D、能理解自然语言 24.人们把以___B___为硬件基本部件的计算机系统称为第三代计算机。 A、ROM B、中小规模集成电路 C、大规模集成电路 D、ROM和RAM 25.在计算机内部一般采用___A___代码表示各种数据。 A、二进制 B、八进制 C、十进制 D、十六进制 26.将二进制数1100100转换成八进制数是___B____。 A、123 B、144 C、80 D、800 27.从目前计算机的发展方向看，小型机将__B___。 A、大型化 B、微型化 C、小型化 D、中型化 28.将二进制数1100100转换成十进制数是___B___。 A、110 B、100 C、101 D、99 29.CPU的中文含义是____C____。 A、运算器 B、控制器 C、中央处理器 D、内存储器 30.通用报表系统中，应具有用户自定义__C___等。 A、数据来源 B、报表项目的算法 C、数据来源、打印格式 D、数据来源、报表项目的算法、打印格式 31.二进制数1011所对应的十进制数是___B___。 A、9 B、11 C、12 D、13 32.完整的计算机系统应包括___C___。 A、主机和外设 B、系统软件和应用软件 C、硬件系统和软件系统 D、存储器、控制器、运算器和输入／输出设备 33.计算机的硬件组成主要包括：总线、中央处理器、输入／输出设备和__D__。 A、内存 B、磁盘 C、光盘 D、存储器 34.微型计算机的运算器、控制器、内存储器的总称是___B___。 A、外设 B、主机 C、CPU D、硬件系统 35.中央处理器主要包括____C____。 A、内存储器和控制器 B、内存储器和运算器 C、运算器和控制器 D、存储器、运算器和控制器 36.微型计算机的核心是___D___。 A、存储器 B、运算器 C、控制器 D、处理器 37.在微机中，运算器的主要功能是_C_。 A、算术运算 B、逻辑运算 C、算术运算和逻辑运算 D、信息处理 38.计算机的存储器是___D___。 A、输入设备 B、输出设备 C、运算装置 D、记忆装置 39.在微机中运行某程序时，若存储容量不够，可解决的正确途径是__D___。 A、增加可使用的外存 B、把软盘换为硬盘 C、把磁盘换为光盘 D、增加可使用的内存 40.下列叙述中不正确的是___B___。 A、32位微机的字长为4个字节 B、内存容量32MB＝32×1000000B C、计算机系统必须由硬件和软件两部分组成 D、计算机程序是各种指令的集合 判断题 1.用于管理计算机资源的软件是操作系统,它负责管理计算机的硬件和调度软件的运行。（ Y ） 2.Windows98中工具栏是由一系列小图标组成，每个小图标对应一个菜单命令。（ Y ） 3.在Windows98中的文件的名字由主文件名与扩展名组成，其中扩展名用来反映文件的类型，因此每一个文件必须指定一个扩展名，没有扩展名的文件是非法的。（ N ） 4.文件夹中还可以包含子文件夹，而最终的文件夹中一般总是有文件的。（ N ） 5.在对话框中，用户可以从一组选项按钮中选两个或两个以上选项。（ Y ） 6.在二进制中：111-101=1（ N ） 7.在Windows98"我的电脑"中可以双击图标把它打开成一个窗口。（ Y ） 8.在Windows98桌面上用鼠标左键单击"我的电脑"图标，就可以打开"我的电脑"窗口。（ N ） 9.要显示窗口中的状态栏，在我的电脑窗口中选中"编辑"菜单中的"状态栏"命令。（ N ） 10.单击"开始"按钮，在菜单中选择"关闭系统"即可退出Windows98。（ N ） 11.在Windows98中文件的扩展名最多由三个字符组成。（ Y ） 12.计算机系统主要由硬件系统和软件系统组成。（ Y ） 13.计算机系统指的就是计算机的硬件,就是看得见,摸得着的实物。（ N ） 14.把鼠标指针移动到文字框中并单击鼠标左键，就可把插入光标移进文字框。（ Y ） 15.启动资源管理器的方法是：单击"开始"按钮，从中选择"资源管理器"，就会看到"资源管理器"窗口。（ N ） 16.计算机以数字形式表示处理信息。（ N ） 17.要选定多个非连续文件或文件夹，可按住Shift键，然后依次单击不连续的各个项。（ N ） 18.删除文件或文件夹最简单的方法是，先选定要删除的文件或文件夹，然后按Delete键。（ N ） 19.要改变一个文件或文件夹的名字，最简单的方法是，选定要更名的文件或文件夹，然后双击该文件或文件夹的名字，出现一个方框，从中输入新的文件或文件夹名。（ N ） 20.在安装中文Windows98后，系统所带的汉字字体只有"宋体"和"黑体"两种字体。（ N ） 第七套 选择题 第1题、Word应用程序窗口中的“标尺”工具栏，一般情况下，可以通过___C___进行设定与取消。 A、“工具”菜单中的“?”命令 B、“文件”菜单中的“标尺” C、“视图”菜单中的“标尺” D、“视图”菜单中的“工具栏” 第2题、一个汉字的___A___不是唯一的。 A、输入码 B、机内码 C、国标码 D、区位码 第3题、在当前文档中，若需插人Windows的图片，应将光标移到插入位置，然后选择___B____。 A、“插入”菜单中的“对象”命令 B、“插入”菜单中的“图片”命令 C、“编辑”菜单中的“图片”命令 D、“文件”菜单中的“新建”命令 第4题、笔记本计算机属于第____ D ___代计算机。 A、一 B、二 C、三 D、四 第5题、根据ISO对数据所下的定义，可认为____ C ___都是数据。 A、声音和磁盘 B、数字和网络 C、数字、图画、声音和活动图像 D、数字、图画和内存 第6题、会计核算软件的会计数据输入可以采用___ D ___形式。 A、键盘手工输入 B、软盘输入、网络传输 C、键盘手工输入、软盘输入 D、键盘手工输入、软盘输入、网络传输等 第7题、会计核算软件应提供符合国家统一___ B ___规定的自动编制会计报表的功能。 A、财经制度 B、会计制度 C、税务制度 D、会计法规 第8题、在Excel97中图表类型有___ B ___种。 A、9 B、14 C、15 D、16 第9题、第一代计算机主要特征是逻辑部件采用___ A ___。 A、电子管 B、晶体管 C、中小规模集成电路 D、大规模和超大规模集成电路 第10题、十进制数12所对应的二进制数是___ C ___。 A、1111 B、1110 C、1100 D、1000 第11题、PC机属于___ C ___。 A、工作站 B、中西文打字机 C、个人计算机 D、计算器 第12题、在撰写长篇文章时，为了保证文章各部分内容格式的一致，最好使用Word的____ B ___功能。 A、节 B、样式 C、模板 D、表格 第13题、双击Word窗口的标题栏时，会产生的效果是使___ D ___。 A、窗口最大化 B、窗口关闭 C、窗口还原 D、窗口最大化或窗口还原 第14题、下面是会计数据处理的一般流程，正确的是___ D ___。 A、会计数据的输入、存储、输出 B、会计数据的输入、存储、处理 C、会计数据的存储、处理、输出 D、会计数据的输入、存储、处理、输出 第15题、在一张表格中，在对同一列三个连续单元格做合并的前提下，然后再拆分此单元格，则行数可选择的数字为___ A ___。 A、1和3 B、2和3 C、1和2 和3 D、以上均不对 第16题、Word应用程序窗口中的各种工具栏可以通过__ A ___进行增减。 A、“视图”菜单中的“工具栏”命令 B、“文件”菜单中的“属性”命令 C、“工具”菜单中的“选项”命令 D、“文件”菜单中的“页面设置”命令 第17题、在Word中，丰富的特殊符号是通过___ C ___输人的。 A、“格式”菜单中的“插人符号”命令 B、专门的符号按钮 C、“插人”菜单中的“符号”命令 D、在“区位码”方式下 第18题、Word的界面并不是一成不变的，下列改变界面的操作中错误的是___ C __。 A、选择“工具”菜单下的“选项…”，可以控制滚动条是否显示 B、选择“工具”菜单下的“自定义…”，可以设置菜单项目对应的快捷键 C、选择“格式”菜单下的“样式…”，可以调出“艺术字”工具箱 D、用鼠标右键单击工具栏任意位置，可以设置工具栏显示项目 第19题、为了便于在文档中查找信息，可以使用___ D ___符号来代表任何一个字符进行匹配。 A、* B、& C、% D、? 第20题、关于操作人员分工的叙述，不正确的是___ D ___。 A、避免与业务无关的人员和无权限的人员进行非法操作 B、严格执行内部控制制度 C、保证系统的安全性和会计数据的保密性 D、减轻个人负担，发挥集体的力量 第21题、多媒体中的文本一般为超文本，它是一种非线性的 __ A ___ 结构。 A、网状 B、层次 C、总线 D、星形 第22题、当今许多西方发达国家，已将计算机广泛应用于___ D ___。 A、会计数据处理 B、会计管理 C、财务管理以及预测和决策 D、会计数据处理、管理、预测和决策 第23题、记帐凭证的编号可以采用___ C ___。 A、手工输入 B、会计软件自动生成 C、手工输入、会计软件自动生成 D、其他方法 第24题、已登帐的记帐凭证，若发现错误，___ B ___直接对该凭证进行修改。 A、审核人员可以 B、不可以 C、可以 D、经批准可以 第25题、ERP是一个___ B ___管理信息系统。 A、制造业 B、有机集成的分布式 C、计算机集成制造 D、计算机辅助设计 第26题、二进制数11101101转换为十六进制数是___ B ___。 A、144 B、ED C、EB D、164 第27题、MRPII即制造资源规划，它包括___ D ___等。 A、营销 B、财务 C、营销、制造 D、营销、制造和财务 第28题、会计报表上的数据如出现错误，应___ B ___报表数据。 A、直接修改 B、间接修改 C、随意修改 D、禁止修改 第29题、计算机用于水电站厂房的设计属于计算机____ B __应用。 A、自动控制 B、辅助设计 C、数值计算 D、人工智能 第30题、计算机数据处理指的是___ C ___ 。 A、数据的录入和打印 B、数据的计算 C、数据的收集、加工、存储和传送的过程 D、数据库 第31题、进行数据恢复后，须重新建立的文件是___ A ___。 A、索引文件 B、随机文件 C、顺序文件 D、磁盘文件 第32题、会计软件产业负责会计软件的___ C ___工作。 A、开发 B、开发、销售 C、开发、销售、售后服务 D、开发、售后服务 第33题、二进制数10100101转换为十六进制数是__ D ___。 A、105 B、95 C、125 D、A5 第34题、计算机发展经历了四代，以前“代”的划分主要根据计算机的___ D __。 A、运算速度 B、应用范围 C、功能 D、主要逻辑元件 第35题、计算机目前应用于财务管理、数据统计、办公自动化、情报检索等领域，这些领域可归结为___ D ___领域。 A、辅助设计 B、实时控制 C、科学计算 D、数据处理 第36题、微机断电后，____ B ___存储器所存数据会全部丢失。 A、ROM B、RAM C、硬盘 D、软盘 第37题、当前使用的微型计算机，其主要元器件是由___ C ___构成的。 A、晶体管 B、小规模集成电路 C、大规模和超大规模集成电路 D、电子管 第38题、下列汉字编码中，用于汉字输出的是___ C ___。 A、区位码 B、国标码 C、字形码 D、机内码 第39题、计算机应用最广泛的领域是___ B ___。 A、辅助设计 B、信息处理 C、过程控制 D、数值计算 第40题、对以下的Windows98与Word操作，描述正确的是___ A ___。 A、从软盘上删除的文件与文件夹，不送到回收站 B、在同一个文件央中，可以创建两个同类型的同名文件 C、删除了某应用程序的快捷键，将删除此应用程序对应的文件 D、不能打开两个Word应用程序窗口 判断题 第1题、会计科目编码是在计算机运用于会计工作以后提出的。（N） 第2题、“画图/椭圆”工具在默认情况下画出的是椭圆。（Y） 第3题、数据保密性是指任何人无法取得会计信息。（N） 第4题、在Windows98中移动文件将会将文件放置到新的位置并且删除旧位置上的原始文件。（Y） 第5题、Windows系统是一个数据管理系统。（N） 第6题、手工会计与电算化会计在信息系统方面的基本功能不一致。（N） 第7题、数据处理是计算机目前应用最多的领域。（Y） 第8题、使用“铅笔”工具作图时，可以选择线的宽度及样式。（N） 第9题、进入写字板后，如果看不到工具条、格式栏和状态栏，则可以在“编辑”菜单中选择相应的项来显示这些栏目。（N） 第10题、科学计算是计算机最早的应用领域。（Y） 第11题、在Windows系统中,对文档窗口的切换可用Alt+Tab进行。（N） 第12题、单机系统独立性强，数据共享性差，但整体工作效率比多机联网系统高。（N） 第13题、手工会计与电算化会计所采用的簿记规则不同。（N） 第14题、计算机内部数字的表示是十进制形式。（N） 第15题、写字板包含剪切、复制和粘贴功能，但不包含查找和替换功能。（N） 第16题、科学计算是计算机目前应用最多的领域。（N） 第17题、记事本是最简单的文本编辑软件，建立的文本文件，不能设置字体与字号。（N） 第18题、附件中的计算器有两种基本类型：标准计算器和科学计算器。（Y） 第19题、在Windows98的MS-DOS方式下，不再可以执行原来DOS系统中的绝大多数命令。（N） 第20题、数据处理是计算机最早的应用领域。（N） 第八套 选择题 1.会计数据输出的常用方式有___D___。 A、显示输出 B、打印输出 C、磁性介质输出 D、A+B+C 2.在Word中，在正文中选定一矩形区域的操作是___A___。 A、先按住[Alt]键，然后拖动鼠标 B、先按住[Ctrl]键，然后拖动鼠标 C、先按住[Shift]键，然后拖动鼠标 D、先按住[Alt]+[Shift]键，然后拖动鼠标 3.设置会计科目编码要求___B___。 A、可以任意设置 B、一级科目编码应按财政部统一规定 C、必须按财政部统一规定 D、各级科目编码长度要相同 4、制定会计核算软件基本功能规范的根据是___D___。 A、《中华人民共和国会计法》和《会计电算化工作规范》 B、《会计电算化工作规范》 C、《会计电算化管理办法》 D、《中华人民共和国会计法》和《会计电算化管理办法》 5、财政部制定的第一个全国性
摄影技巧大汇总 摄影原理 相机操作 拍摄技巧 思维导图.png
05-16
非常详细的资源，历时三天整理。摄影技巧学习 机器上的参数 镜头上的 OIS 相机上的 为什么要用取景器？ 没有取景器的微单拍摄，在以下场景非常苦恼： 1、强光下 2、老花眼，尤其是我这样37岁就开始老花眼的人 3、尤其是长焦拍摄，需要稳定的状态下。单反相机机身和脸部是一个重要的支撑点。 4、液晶取景非常费电，为了抓拍又不能随时关机，得多带几块电池。 除非在看取景器非常困难的情况下需要显示屏辅助取景（比如相机高度已高过头顶或机位很低）一般情况还是看取景器。 1是因为取景器是光学成像，镜头所拍摄的东西通过相机里的反光板能一点不差的传送到眼睛里，显示屏是电子的，从真实度和清晰度都不如取景器。 2显示屏取景更费电，如果出门拍摄一天都用显示器取景会很费电。 3一般单反相机在显示屏模式下按下快门时，快门不是马上释放，而是要有一个1秒钟左右的间隔，如果拍摄移动物体，这个世界可能被摄体已经不在预先构图中预计出现的位置了。 当然，微单用的是电子取景器，这个是要耗电的，不过关掉电子屏还是会节省很多点。 如何关闭自动连接手机传输图像？ 耗电情况如何？ 后期 capture one 后期 导入图片后不能编辑，所有的编辑图标都是灰色的 首选项-图像-打开JPEG编辑、打开tiff编辑、打开png编辑都勾上。 没找着 打开JPEG编辑 然后，查看英文界面发现乃session一词，就是允许用户直接访问硬盘上的图像文件并对其直接操作的意思。 这个功能是C1与LR的最大不同之一，用LR时，不导入就无法对图像进行编辑调整，而C1用户则可在会话的方式下，直接查看硬盘的目录树，在任意位置上打开图像文件。 然后，从目录树里直接选择图像文件并打开编辑，会话是首选。当用此法查看图像时，也会在图像所在的文件夹里同时生成一个CaptureOne子文件夹。 是不是和图层有关？ 也无法联机拍摄？ 是不是xt30不支持 是不是和激活不成功有关？ 重新激活pro模式 c1 的几种模式 Express版本免费提供给Sony用户使用（在Pro for Sony的基础上，对有一些功能进行了阉割）； Pro for Sony为收费版本，功能与Capture One Pro一样，但是只支持Sony机器。 DB版本免费提供给Phase One和Leaf的数码后背用户使用，不支持135系列相机。 Capture One Pro的售价为239欧元/279美刀（国内售价2390元），支持市场上绝大部分的135相机和数码后背（据我的经验来看，只不支持宾得），功能最为齐全。 如何查看已经激活？ 重新安装 Capture One有几个核心功能： 1.最好的Raw格式解析算法 2.最好的联机拍摄（商业摄影师联机拍摄首选） 3.颜色编辑器 4.图层遮罩 5.关键字管理（Capture One Pro 9新功能） 6.与PS、LR相比，Capture One 提供了另外的一套后期思路，在我看来学习Capture One的成本要比LR低，但因为国内相关教程较少，所以Capture One在中国的用户没有LR的多，知名度也没有LR的高。 通俗讲capture one的优势 Capture One 可以创建属于你自己的色彩管理文件 Capture One 可以让你马上看到画面中对焦对实了的部分 有点像观看照片时的峰值 Capture One 可以用色彩编辑器做你想做的关于色彩的一切调节 Capture One 联机拍摄无人能比 还可以用iPad或iPhone无线实时监看画面 拿过去给模特看 做动作或表情调整 ram格式是个什么格式？ affinity photo 拍摄技巧 如何保持手持拍摄？ ①双手握持三点接触法 ②贴身握机发 ③颈部拉直肩带发 能拍一些平移的画面 ④机身防抖 ⑤后期 ⑥人肉独脚架（利用重力下坠） ⑦广角拍摄,短焦开启防抖 ⑧拍成慢动作，也能防抖 用更高的帧数 其他 有时手持拍摄也是有独特的效果的 机器拍摄 画面有点不自然，有点假 光圈快门感光度调节顺序 首先根据需要的景深选择光圈， 用光圈优先模式：这样快门速度就自动了。 这个曝光只能由相机自动决定，差不了太多。 大多数摄影师大多数场景常用光圈优先模式拍摄？ 如何设置为光圈优先？ 根据物体移动速度选快门速度， 快门速度会适合抓拍，或者是记录轨迹 如果用快门优先模式，可以设置相对比较快的快门速度，光圈自动，同样能满足大部分拍摄。 最后根据需要的曝光选感光度。 B什么意思？ 曝光补偿和感光度的区别？ 元素要少！（做减法） 元素统一 云和天空 人为产生的元素 黑夜会弱化掉所有的元素，只留下点亮的那些东西 减法 虚化 虚化了背景，统一了元素 元素划分 调色上做减法 处理前 处理后（去掉了几种颜色） 处理前 处理后 对焦 如何手动对焦？ 想要收获最好的虚化效果，要达到以下三个条件 手动对焦一般都是在一些很极限的情况下才会用了。 不要太在意专业啊、手动啊啥的，千万别以为手动就是专业的，自动对焦本身就是技术的进步，没有那个摄影师会在自动能满足的情况下去考虑手动对焦，除非是职业装13的。 手动对焦适用场合大致如下： 1、弱光环境 很多拍星空的朋友都有这样的体验，当你想拍摄清晰的前景，对远处暗淡的主体对焦时，你半按快门，却发觉相机无法对焦。 在低光低对比的环境下，相机是无法准确对焦的，此时，手动对焦便是最好的选择。 2、微距拍摄 　　近距离拍摄物体，半按快门，图像一直在对焦和失焦之间徘徊，始终无法全按快门拍照，此时是最尴尬的时刻，这是因为景深太浅，导致相机无法自动对焦。 这时使用手动对焦就可以解决大部分问题。 3、主体前有遮挡物 　　在一些场合，你想拍摄的被摄主体前面，有其他物体在前景位置遮挡，比如栏杆，玻璃等等，自动对焦往往就会将焦点放在前景物体上，而不是你想拍摄的主体，此时，用手动对焦能快速解决问题。 4、使用老镜头 　　老镜头多没有自动对焦模式，只支持手动对焦，此时便毫无其他选择了。 5、摄影乐趣 以前很喜欢蔡司镜头，它拍出的图片色彩浓郁，德味甚浓，但蔡司头都是手动头。 犹豫再三，半年前还是禁不住诱惑进了一只蔡司50/1.4镜头。 其后，我多次用它进行街拍或人像拍摄，不得不说，手动对焦的乐趣，是旁人无法体会的。 二、手动对焦方法 1、相机设置：（以尼康相机为例） 1.1.镜头的对焦模式，调为手动，即 “M”档。 1.2.相机的对焦模式，调为手动，即 “M”档。 1.3.另外，我拍摄风光类题材，相机的拍摄模式也是手动“M”档。 2、对焦点选择： 2.1.静态风光摄影中，一般选择全景深的近三分位对焦。 2.2.城市夜景风光，对焦部位尽量选择窗户等相对高光比区域，便于合焦确认。 2.3.强光手电辅助照亮主体，也是手动快速对焦的法宝。 3、手动对焦方法： 3.1.稳定：使用三角架等设备固定相机。 3.2.光圈：一般风光摄影的光圈设置为F8-F16，在对焦时，先把它设置为镜头的最大光圈，以得到最浅景深便于合焦识别。这一步是手动精准对焦的关键！ 3.3.打开相机背屏显示模式： 3.4.选择对焦点： 左右上下移动背屏上的红色方块，来选择对焦点。 3.5.最大限度放大对焦点： 按相机上的放大键，最大限度放大对焦点。 3.6.手动转动镜头的对焦环，调节到对焦点最清晰为止。 3.7.把光圈设置再调整回实拍光圈，即F8-F16。 3.8.手动对焦完毕，可以实拍。 其他的合焦确认方法： 1、相机合焦提示 调节对焦环，观察单反相机目镜，里面有合焦显示提示。尼康相机是白色的圆点，没有合焦时，是向右或向左的白色三角。 2、峰值对焦 峰值对焦是索尼微单相机所具备的一种对焦方式，其原理是将画面对比度最高的区域用高亮的方式显示出来。越是接近合焦，画面上出现的红色（颜色也可设定为其他颜色）颗粒就越是明显。而这些红色的颗粒就是所谓的峰值。 对焦环 如何手动对焦？ 想要收获最好的虚化效果，要达到以下三个条件 手动对焦一般都是在一些很极限的情况下才会用了。 不要太在意专业啊、手动啊啥的，千万别以为手动就是专业的，自动对焦本身就是技术的进步，没有那个摄影师会在自动能满足的情况下去考虑手动对焦，除非是职业装13的。 手动对焦适用场合大致如下： 1、弱光环境 很多拍星空的朋友都有这样的体验，当你想拍摄清晰的前景，对远处暗淡的主体对焦时，你半按快门，却发觉相机无法对焦。 在低光低对比的环境下，相机是无法准确对焦的，此时，手动对焦便是最好的选择。 2、微距拍摄 　　近距离拍摄物体，半按快门，图像一直在对焦和失焦之间徘徊，始终无法全按快门拍照，此时是最尴尬的时刻，这是因为景深太浅，导致相机无法自动对焦。 这时使用手动对焦就可以解决大部分问题。 3、主体前有遮挡物 　　在一些场合，你想拍摄的被摄主体前面，有其他物体在前景位置遮挡，比如栏杆，玻璃等等，自动对焦往往就会将焦点放在前景物体上，而不是你想拍摄的主体，此时，用手动对焦能快速解决问题。 4、使用老镜头 　　老镜头多没有自动对焦模式，只支持手动对焦，此时便毫无其他选择了。 5、摄影乐趣 以前很喜欢蔡司镜头，它拍出的图片色彩浓郁，德味甚浓，但蔡司头都是手动头。 犹豫再三，半年前还是禁不住诱惑进了一只蔡司50/1.4镜头。 其后，我多次用它进行街拍或人像拍摄，不得不说，手动对焦的乐趣，是旁人无法体会的。 二、手动对焦方法 1、相机设置：（以尼康相机为例） 1.1.镜头的对焦模式，调为手动，即 “M”档。 1.2.相机的对焦模式，调为手动，即 “M”档。 1.3.另外，我拍摄风光类题材，相机的拍摄模式也是手动“M”档。 2、对焦点选择： 2.1.静态风光摄影中，一般选择全景深的近三分位对焦。 2.2.城市夜景风光，对焦部位尽量选择窗户等相对高光比区域，便于合焦确认。 2.3.强光手电辅助照亮主体，也是手动快速对焦的法宝。 3、手动对焦方法： 3.1.稳定：使用三角架等设备固定相机。 3.2.光圈：一般风光摄影的光圈设置为F8-F16，在对焦时，先把它设置为镜头的最大光圈，以得到最浅景深便于合焦识别。这一步是手动精准对焦的关键！ 3.3.打开相机背屏显示模式：
数字图像处理车牌定位开题报告
04-25
上述产品中所使用的汽车图像均为灰度图像，而车牌本身是彩色物体，其底色和字符颜色为有限的几种，具有明显的颜色特征，车牌定位及字符的分割和识别没有用到颜色特征，采用彩色图像模式，目前的算法也很少涉及颜色...
华为校招机试 - 扑克牌消除（20240417）
最新发布
伏城之外的博客
04-18 148
已支持（Java & JS & Python & C & C++），实现：栈结构
洛谷【入门1】顺序结构
weixin_69583420的博客
04-12 645
洛谷【入门1】顺序结构——python
C++ | Leetcode C++题解之第27题移除元素
Ddddddd_158的博客
04-14 474
C++ | Leetcode C++题解之第27题移除元素
模式识别算法matlab
11-10
MATLAB是一种常用的科学计算软件，也是模式识别领域中常用的工具之一。MATLAB提供了许多内置的函数和工具箱，可以用于模式识别算法的实现和应用。以下是一些常用的模式识别算法及其在MATLAB中的实现方式：\n\1. K近邻算法：MATLAB中可以使用fik函数实现K近邻分类器的训练和预测。\n\2. 支持向量机算法：MATLAB中可以使用fisvm函数实现支持向量机分类器的训练和预测。\n\3. 决策树算法：MATLAB中可以使用fir函数实现决策树分类器的训练和预测。\n\4. 随机森林算法：MATLAB中可以使用TrBgger函数实现随机森林分类器的训练和预测。\n\5. 神经网络算法：MATLAB中可以使用fforwar函数实现前馈神经网络的训练和预测。\n\以上是一些常用的模式识别算法及其在MATLAB中的实现方式，当然还有其他的算法和函数可以使用。需要根据具体的问题和数据选择合适的算法和工具。\n\

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 27
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值