%hermite.m
%求埃尔米特多项式和误差估计的MATLAB主程序
%输入的量:X是n+1个节点(x_i,y_i)(i = 1,2, ... , n+1)横坐标向量,Y是纵坐标向量,
%以f'(x_i)=y'_i(i = 1,2,...,n+1)为元素的向量Y1;
%x是以向量形式输入的m个插值点,M在[a,b]上满足|f~(2n+2)(x)|≤M
%注:f~(2n+2)(x)表示f(x)的2n+2阶导数
%输出的量:向量y是向量x处的插值,误差限R,2n+1阶埃尔米特插值多项式H_k及其系数向量
%H_c,误差公式wcgs及其系数向量Cw.
function[y,R,Hc,Hk,wcgs,Cw] = hermite(X,Y,Y1,x,M)
n = length(X);
m = length(x);
for t = 1 : m
z = x(t);
H = 0;
q = 1;
c1 = 1;
for k = 1 : n
s = 0;
V = 1;
for i = 1 : n
if k ~= i
s = s + (1/(X(k)-X(i)));
V = conv(V,poly(X(i)))/(X(k)-X(i));
end
end
h = poly(X(k));
g = ([0 1]-2 * h * s);%注意不要写成1-2*h*s,因为是多项式减法,低阶多项式前面必须用零填补,书上的错误,浪费我一晚上时间
G = g * Y(k) + h * Y1(k);
H = H + conv(G,conv(V,V));%hermite插值多项式
b = poly(X(k));
b2 = conv(b,b);
q = conv(q,b2);
end
Hc = H;
Hk = poly2sym(H);
Q = poly2sym(q);
for i = 1 : 2*n
c1 = c1 * i;
end
wcgs = M * Q / c1;
Cw = M * q / c1;
y(t) = polyval(Hc,x(t));
R(t) = polyval(Cw,x(t));
end
%hermite.m
%求埃尔米特多项式和误差估计的MATLAB主程序
%输入的量:X是n+1个节点(x_i,y_i)(i = 1,2, ... , n+1)横坐标向量,Y是纵坐标向量,
%以f'(x_i)=y'_i(i = 1,2,...,n+1)为元素的向量Y1;
%x是以向量形式输入的m个插值点,M在[a,b]上满足|f~(2n+2)(x)|≤M
%注:f~(2n+2)(x)表示f(x)的2n+2阶导数
%输出的量:向量y是向量x处的插值,误差限R,2n+1阶埃尔米特插值多项式H_k及其系数向量
%H_c,误差公式wcgs及其系数向量Cw.
function[y,R,Hc,Hk,wcgs,Cw] = hermite(X,Y,Y1,x,M)
n = length(X);
m = length(x);
for t = 1 : m
z = x(t);
H = 0;
q = 1;
c1 = 1;
for k = 1 : n
s = 0;
V = 1;
for i = 1 : n
if k ~= i
s = s + (1/(X(k)-X(i)));
V = conv(V,poly(X(i)))/(X(k)-X(i));
end
end
h = poly(X(k));
g = ([0 1]-2 * h * s);%注意不要写成1-2*h*s,因为是多项式减法,低阶多项式前面必须用零填补,书上的错误,浪费我一晚上时间
G = g * Y(k) + h * Y1(k);
H = H + conv(G,conv(V,V));%hermite插值多项式
b = poly(X(k));
b2 = conv(b,b);
q = conv(q,b2);
end
Hc = H;
Hk = poly2sym(H);
Q = poly2sym(q);
for i = 1 : 2*n
c1 = c1 * i;
end
wcgs = M * Q / c1;
Cw = M * q / c1;
y(t) = polyval(Hc,x(t));
R(t) = polyval(Cw,x(t));
end
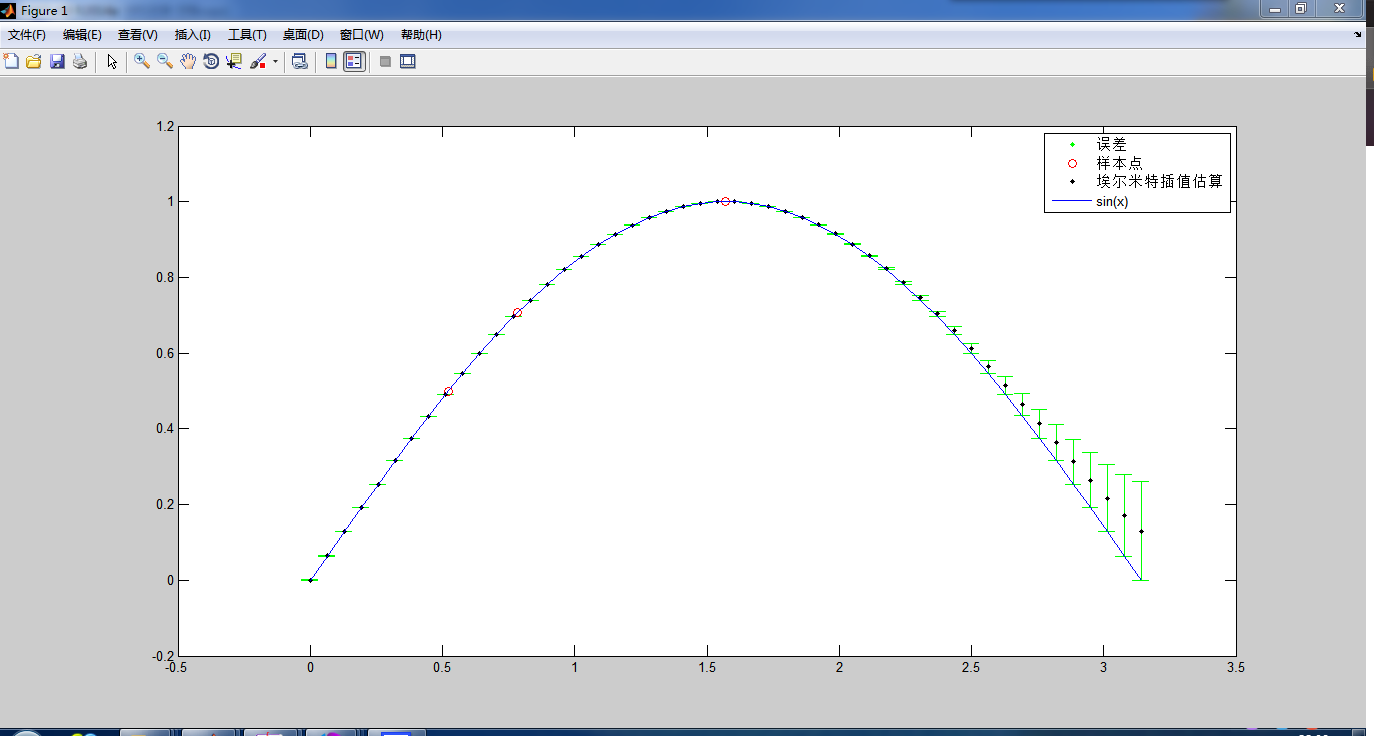
从这图片看要比拉格朗日和牛顿插值要好,不过当插值多了以后,也就是埃尔米特多项式的次数高了以后误差会变得很大的。不信我们来试试。
我们还是用sinx,不过这次我们用5个点。
X 0 pi/6 pi/4 pi/3 pi/2
Y 0 0.5 0.7071 0.8660 1
Y1 1 0.8660 0.7071 0.5 0
>> X = [0 pi/6 pi/4 pi/3 pi/2];Y = [0 0.5 0.7071 0.8660 1];Y1 = [1 0.8660 0.7071 0.5 0];
>> M = 1;
>> x = linspace(0, pi, 50);
>> [y,R,Hc,Hk,wcgs,Cw] = hermite(X,Y,Y1,x,M)
>> y1 = sin(x);
>> errorbar(x,y,R,'.g')
>> hold on
>> plot(X, Y, 'or', x, y, '.k', x, y1, '-b');
>> legend('误差','样本点','埃尔米特插值估算','sin(x)'); 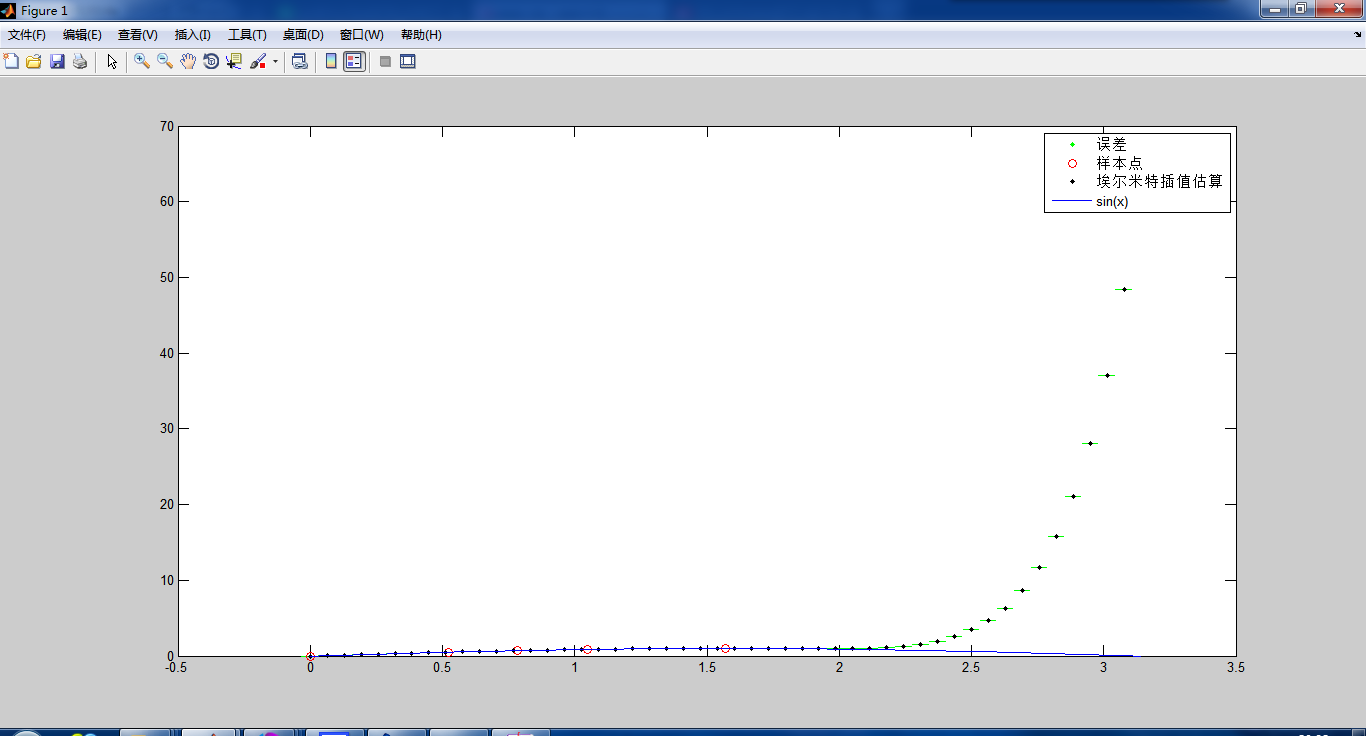
可以看到拟合的多项式从x=2.5开始远远偏离sinx,并且此时误差公式也失效了.这就是我们后面需要讲到的高次插值的振荡问题。
































 1565
1565

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








