降维问题在很久以前就接触了,那时候也会用协方差矩阵实现PCA来实现降维,可以应用在图像压缩和数据维度缩减,减少噪声数据等。但是最近在用sklearn的pca工具实现降维时候发现这儿的pca降得到的维度只能小于等于样本数和维度的最小值( 降维后的维度为k,原始数据样本数为m,维度为n,则k≤min(m,n) )。在这儿就不懂了,其实查了很多资料后也是理解了大部分,但对sklean上降低的维度到样本数和维度以下还是存在疑惑。
首先,心中有疑惑,才有寻求答案的动力,才有探寻真理的动力。
疑惑一:为什么实现pca需要用协方差矩阵?
疑惑二:用svd实现降维和用协方差实现有什么关联?
首先介绍实现pca有两种方案,第一个是特征值分解,第二个是奇异值分解
其中特征值分解是通过协方差矩阵来实现的
pca的实现思路也有两种解释:
1、第一种是最大可分性:使得投影点在超平面上的投影尽可能分开
2、第二种是最近重构性:使得样本点到超平面的距离都足够近
这儿假设数据是
X=m∗n
的,m代表样本数,n代表维度数。那么一般实现pca的流程是这样的
1、对数据标准归一化(去均值,各维度统一方差,将各维度在统一尺度上计算)
2、计算协方差矩阵
C=1/(m−1)XTX
3、计算C的特征向量矩阵和特征值,将特征值对应的特征向量按照特征值由大到小排列得到特征向量矩阵,取前k列特征向量组成投影矩阵
Ureduce
4、计算降维后的数据
Xnew=X∗Ureduce
5、这样就将n维的矩阵降到k维
以上的实现方法是基于特征值分解的,那么为什么pca还可以用svd来实现呢?
SVD(奇异值分解)是对矩阵分解的一种方法,
X=USVT
其中X是m*n的矩阵,U是m*m的矩阵,它是由
XXT的特征向量构成的
,S是m*n维的矩阵,它是一个对角矩阵,V类似于U,它是由
XTX
的特征向量构成的,其中U,V都是酉矩阵(都是实数的话就是正交矩阵)
这儿可以将协方差矩阵C进行奇异值分解来降维,也可以直接对X来奇异值分解降维。
1、对X进行svd,得到的V( XTX 的特征向量矩阵)就是C对应的特征向量矩阵,由于svd得到的奇异值正好是从大到小进行排列,那么这儿得到的U正好是与特征值大小顺序对应构成的特征向量。为什么V是C的Q(特征向量矩阵)呢?
解释:
首先说明 特征分解
XTX=Q⋀Q−1
,其中Q是特征向量矩阵,
⋀
是特征值构成的对角矩阵。
X=USVT
那么
C=XTX=(USVT)TUSVT=VS2VT=VS2V−1
这儿发现
V=Q,⋀=S2
还可以从另一个角度看,V本来就是 XTX 的特征向量矩阵呀
2、对
XTX
进行svd,得到的U就是X的特征向量矩阵。
看完上面用协方差矩阵和
SVD
来实现降维,那么为什么用
SVD
呢?这儿主要是当维度
n
很高时,得到的协方差矩阵是一个
参考文献:
Andrew NG 的CS229
http://justdark.github.io/%E5%8D%9A%E5%AE%A2/2016/11/12/pca_svd_recall/
http://blog.csdn.net/wangjian1204/article/details/50642732
http://blog.csdn.net/babywong/article/details/50085239
2017.11.24更新———————————————–
今天通过python实现了下使用协方差矩阵对cifar中49张图片降维。
import matplotlib.pyplot as plt
import numpy as np
def unpickle(file):
import pickle
with open(file, 'rb') as fo:
dict = pickle.load(fo, encoding='bytes')
return dict
def show(imgs):
matrix=np.zeros(shape=(7*32,7*32,3),dtype=np.uint8)
print(matrix.shape)
print(imgs[0].shape)
index=-1
for i in range(7):
for j in range(7):
index+=1
matrix[i*32:(i+1)*32,j*32:(j+1)*32,:]=imgs[index]
plt.imshow(matrix)
plt.show()
def pca(imgs_raw):
'''
:param imgs: 49*3072
:return:
'''
imgs_raw=imgs_raw.astype(np.float32)
imgs=imgs_raw-np.mean(imgs_raw,axis=0)
cov=np.dot(imgs.T,imgs)/(imgs.shape[0]*imgs.shape[1])
U,S,V=np.linalg.svd(cov)
# 去相关
# imgs=np.dot(imgs,U)
# 降维
imgs_pca=np.dot(imgs,U[:,:30])
imgs_pca_r=np.dot(imgs_pca,U[:,:30].T)
imgs_pca_r+=np.mean(imgs_raw,0)
imgs_pca_r = imgs_pca_r.reshape((len(imgs), 3, 32, 32)).transpose(0, 2, 3, 1)
show(imgs_pca_r)
# imgs = imgs.reshape((len(imgs), 3, 32, 32)).transpose(0, 2, 3, 1)
if __name__ == '__main__':
data_labels=unpickle('H:\\Machine Learning\\'
'deep-learning-master\\deep-learning-master\\image-classification\\cifar-10-batches-py\\data_batch_1')
imgs=data_labels[b'data'][:49]
pca(imgs)
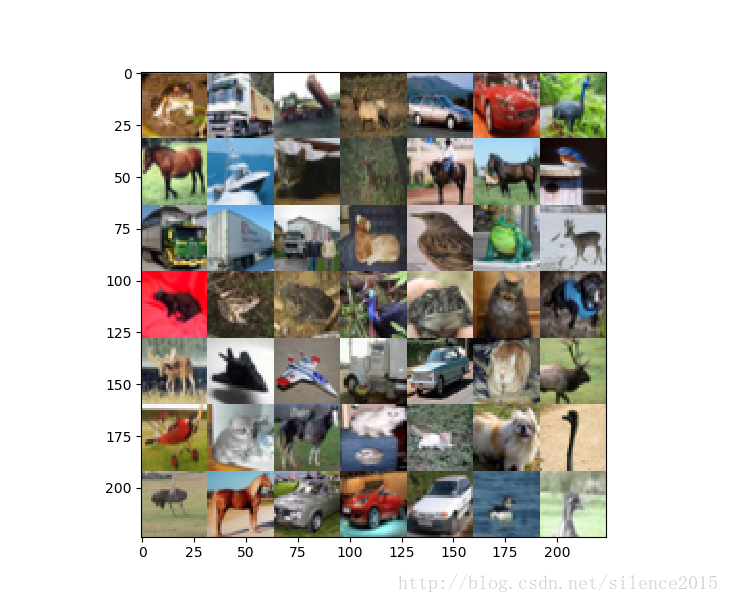
# show(imgs)第一张是原图:
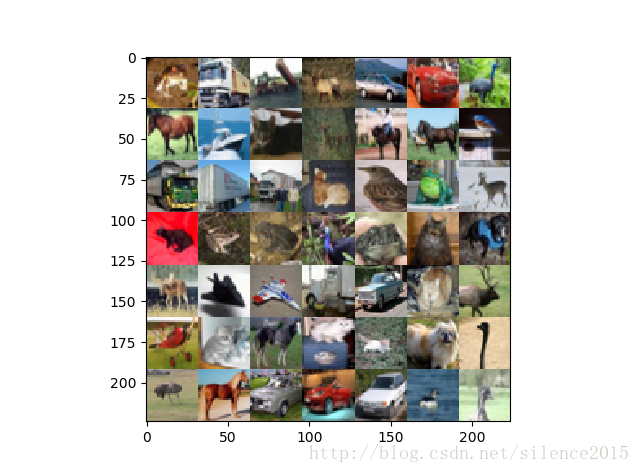
第二张是降维到50维度的样子:
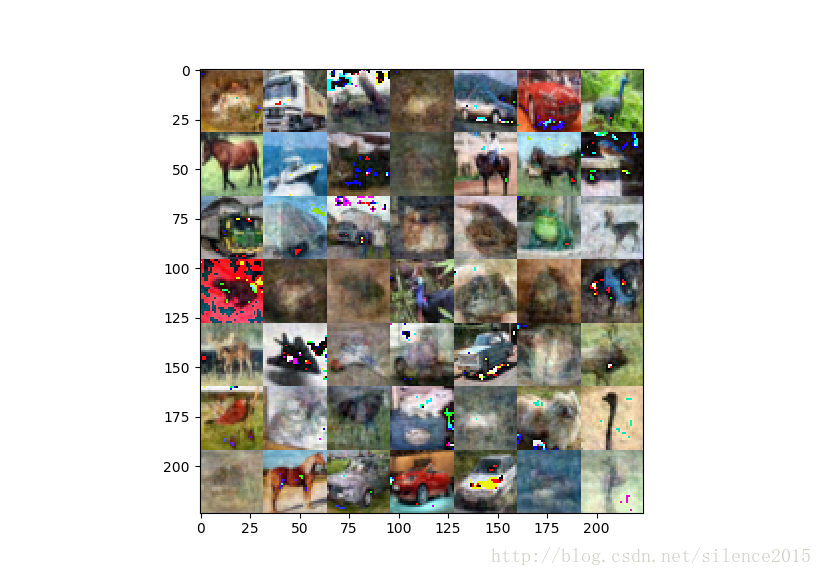
第三张是降维到30维度的样子:























 379
379

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








