分类算法 之 逻辑回归–理论+案例+代码
标签(空格分隔): SPARK机器学习
1. 逻辑回归概述
1.1 概述
逻辑回归与线性回归类似,但它不属于回归分析家族(主要为二分类),而属于分类家族,差异主要在于变量不同,因此其解法与生成曲线也不尽相同。
逻辑回归是无监督学习的一个重要算法,对某些数据与事物的归属(分到哪个类别)及可能性(分到某一类别的概率)进行评估。
1.2 使用
在医学界,广泛应用于流行病学中,比如探索某个疾病的危险因素,根据危险因素预测疾病是否发生,与发生的概率。
比如探讨胃癌,可以选择两组人群,一组是胃癌患者,一组是非胃癌患者。因变量是“是否胃癌”,这里“是”与“否”就是要研究的两个分类类别。自变量是两组人群的年龄,性别,饮食习惯,等等许多(可以根据经验假设),自变量可以是连续的,也可以是分类的。
在金融界,较为常见的是使用逻辑回归去预测贷款是否会违约,或放贷之前去估计贷款者未来是否会违约或违约的概率。
在消费行业中,也可以被用于预测某个消费者是否会购买某个商品,是否会购买会员卡,从而针对性得对购买概率大的用户发放广告,或代金券等等,进行精准营销。
2. 逻辑分布(Logistic distribution)
设X是连续随机变量,X服从逻辑分布式指X具有下列分布函数和密度函数:
2.1 分布函数

上述公式中, 是一个标准化的过程,μ是均值(位置参数,决定分布的位置),
是一个标准化的过程,μ是均值(位置参数,决定分布的位置), 是标准差(形状参数,标准差越大则分布曲线越扁平,分布越不集中)
是标准差(形状参数,标准差越大则分布曲线越扁平,分布越不集中)

上图为逻辑分布函数的图形,是一条S型曲线(sigmoid curve)。该曲线以点(μ,1/2)为中心对称。曲线在中心附近增长速度较快,在两端增长速度较慢,形状参数的值越小,曲线在中心附近增长得就越快。
2.2 密度函数
密度函数是分布函数的一阶求导,公式与图形如下:


3. 二项逻辑回归模型(binomial logistic regression model)
二项逻辑回归模型是一种分类模型,有条件概率分布P(Y/X)表示,X为取数为实数,Y取值为0或1。研究已知X,求Y为1或0的概率。
3.1 二项逻辑回归模型
模型:

上述公式中,分别表示Y=1和Y=0的概率,Y是输出。
其中,x为输入变量,在机器学习中我们一般称之为feature,特征;w和b为参数,是我们接下来要去估计的,w为权值向量,b为偏置向量,w*x为w与x的内积。
根据以上公式,估计出参数后,输入已知的x值,便可以求出Y为1或0的概率了。两个概率相加为1.
逻辑回归会比较两个概率值的大小,然后将实例X分到概率较大的类别中。
简化模型:
有时,为了方便,我们将权值向量与输入向量将以扩充,即
w=(w0,w2,w3,…,wn,b)^T;
x=(x1,x2,x3,…,xn,1)^T.
^T表示矩阵的转置,那么上述模型可以简写为:

通常情况下,为了更简单只管,我们用z=w*x,那么模型也可以表达如下:
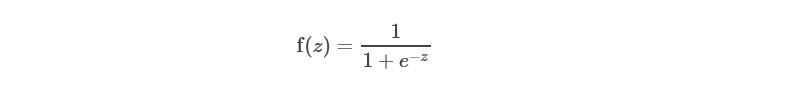
3.2 odds 和 log odds
odds
odds是指事件发生的概率与该事件不发生的概率的比值,如果事件发生的概率为P,不发生的概率为1-P,那么该事件的odds为
odds=




 本文深入介绍了逻辑回归的概念,包括其理论基础、逻辑分布、二项逻辑回归模型和多项逻辑回归模型。此外,还通过Spark MLlib展示了逻辑回归的实际应用,包括数据加载、模型训练、验证和保存。
本文深入介绍了逻辑回归的概念,包括其理论基础、逻辑分布、二项逻辑回归模型和多项逻辑回归模型。此外,还通过Spark MLlib展示了逻辑回归的实际应用,包括数据加载、模型训练、验证和保存。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1030
1030


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







