在数学最优问题中,拉格朗日乘数法(以数学家约瑟夫·路易斯·拉格朗日命名)是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题,其变量不受任何约束。这种方法引入了一种新的标量未知数,即拉格朗日乘数:约束方程的梯度(gradient)的线性组合里每个向量的系数。此方法的证明牵涉到偏微分,全微分或链法,从而找到能让设出的隐函数的微分为零的未知数的值。
定义介绍
设给定二元函数z=ƒ(x,y)和附加条件φ(x,y)=0,为寻找z=ƒ(x,y)在附加条件下的极值点,先做拉格朗日函数
,其中λ为参数。
令F(x,y,λ)对x和y和λ的一阶偏导数等于零,,即
F'x=ƒ'x(x,y)+λφ'x(x,y)=0,
F'y=ƒ'y(x,y)+λφ'y(x,y)=0,
F'λ=φ(x,y)=0
由上述方程组解出x,y及λ,如此求得的(x,y),就是函数z=ƒ(x,y)在附加条件φ(x,y)=0下的可能极值点。
若这样的点唯一,由实际问题,可直接确定此即所求的点。
求极值
求函数f(x,y,z)在条件φ(x,y,z)=0下的极值
方法(步骤)是:
1.做拉格朗日函数L=f(x,y,z)+λφ(x,y,z),λ称拉格朗日乘数
2.求L分别对x,y,z,λ求偏导,得方程组,求出驻点P(x,y,z)
如果这个实际问题的最大或最小值存在,一般说来驻点唯一,于是最值 可求.
条件极值问题也可以化为无条件极值求解,但有些条件关系比较复杂,代换和运算很繁,而相对来说,“拉格朗日乘数法”不需代换,运算简单一点.这就是优势.
条件φ(x,y,z)一定是个等式,不妨设为φ(x,y,z)=m
则再建一个函数g(x,y,z)=φ(x,y,z)-m
g(x,y,z)=0,以g(x,y,z)代替φ(x,y,z)
在许多极值问题中,函数的自变量往往要受到一些条件的限制,比如,要设计一个容积为 V的长方体形开口水箱,确定长、宽和高, 使水箱的表面积最小. 设水箱的长、宽、高分别为 x,y,z, 则水箱容积V=xyz
焊制水箱用去的钢板面积为 S=2xz+2yz+xy
这实际上是求函数 S 在 V 限制下的最小值问题。
这类附有条件限制的极值问题称为条件极值问题,其一般形式是在条件
<!--EndFragment-->
限制下,求函数F的极值
条件极值与无条件极值的区别
条件极值是限制在一个子流形上的极值,条件极值存在时无条件极值不一定存在,即使存在二者也不一定相等。
例如,求马鞍面 z=x.^2-y.^2+1 被平面XOZ 平面所截的曲线上的最低点。
从其几何图形可以看出整个马鞍面没有极值点,但限制在马鞍面被平面 平面所截的曲线上,有极小值 1,这个极小值就称为条件极值。
必要条件
设在约束条件之下求函数的极值。满足约束条件的点 是函数的条件极值点, 且在该点函数满足隐函数存在条件时, 由方程定隐函数 , 于是点就是一元函数的极限点, 有
代入 , 就有
( 以下 均表示相应偏导数在点 的值 . )
Lagrange乘数法 :
由上述讨论可见 , 函数 在约束条件之下的条件极值点应是方程组
的解.
引进所谓Lagrange函数
( 称其中的实数 为Lagrange乘数 )
则上述方程组即为方程组
因此,解决条件极值通常有两种方法
1)直接的方法是从方程组(1)中解出 并将其表示为 代入 消去 成为变量为 的函数将问题化为函数无条件极值问题;
2)在一般情形下,要从方程组(1)中解出 来是困难的,甚至是不可能的,因此上面求解方法往往是行不通的。通常采用的拉格朗日乘数法,是免去解方程组(1)的困难,将求 的条件极值问题化为求下面拉格朗日函数的稳定点问题,然后根据所讨论的实际问题的特性判断出哪些稳定点是所求的极值的。
3)在给定的条件下,若是可以将未知数代换或是解出,则可以将条件极值转化为无条件极值,从而避免引入拉格朗日乘数的麻烦。
注意:▽φ(x,y,z)=0 且 φ(x,y,z)=0的点不会被该方法计算到,因此,若求最大值或最小值时,应把这些点列出来并单独计算。
例题一
抛物面被平面 截成一个椭圆. 求该椭圆到坐标
原点的最长和最短距离.
例3求函数 在条件
下的极小值. 并证明不等式 , 其中 为任意正常数 .
以上面水箱设计为例,看一看拉格朗日乘数法求解条件极值的过程
解: 这个问题的实质是求函数
在条件下的最小值问题, 应用拉格朗日乘法,令
L='2*(x*z+y*z)+x*y+v*(x*y*z-V)';
dLdx=diff(L,'x')
dLdy=diff(L,'y')
dLdz=diff(L,'z')
dLdv=diff(L,'v')
dLdx =2*z+y+v*y*z
dLdy =2*z+x+v*x*z
dLdz =2*x+2*y+v*x*y
dLdv =x*y*z-V
令 L 的各偏导等零,解方程组求稳定点
s1='2*z+y+v*y*z';
s2='2*z+x+v*x*z';
s3='2*x+2*y+v*x*y';
s4='x*y*z-V';
[v,x0,y0,z0]=solve(s1,s2,s3,s4)
v =
[ -2*2^(2/3)/V^(1/3)]
[ -8*(-1/4*2^(1/3)*V^(1/3)+1/4*i*3^(1/2)*2^(1/3)*V^(1/3))^2/V]
[ -8*(-1/4*2^(1/3)*V^(1/3)-1/4*i*3^(1/2)*2^(1/3)*V^(1/3))^2/V]
x0 =[ 2^(1/3)*V^(1/3)]
y0 =[ 2^(1/3)*V^(1/3)]
z0 =[ 1/2*2^(1/3)*V^(1/3)]
这里显然只有实数解才有意义,所以 L 的稳定点只有下面一个
又已知所求的问题确实存在最小值,从而解出的稳定点就是最小值点,即水箱长宽与为高的2倍时用钢板最省。
例题二
再看一个条件极值求解问题
抛物面 被平面 截成一个椭圆,求这个椭圆到坐标原点的最长最短距离。(x73)
解 这个问题的实质是求函数
在条件 与 下的最大、最小值问题,应用拉格朗日乘法,令
L='x^2+y^2+z^2+v*(x^2+y^2-z)+h*(x+y+z-1)';
dLdx=diff(L,'x')
dLdy=diff(L,'y')
dLdz=diff(L,'z')
dLdv=diff(L,'v')
dLdh=diff(L,'h')
dLdx =2*x+2*v*x+h
dLdy =2*y+2*v*y+h
dLdz =2*z-v+h
dLdv =x^2+y^2-z
dLdh =x+y+z-1
s1='2*x+2*v*x+h';
s2='2*y+2*v*y+h';
s3='2*z-v+h';
s4='x^2+y^2-z';
s5='x+y+z-1';
[h,v,x0,y0,z0]=solve(s1,s2,s3,s4,s5);
x0,y0,z0
x0 =
[ 3/4-1/4*i*13^(1/2)]
[ 3/4+1/4*i*13^(1/2)]
[ -1/2+1/2*3^(1/2)]
[ -1/2-1/2*3^(1/2)]
y0 =
[ 3/4+1/4*i*13^(1/2)]
[ 3/4-1/4*i*13^(1/2)]
[ -1/2+1/2*3^(1/2)]
[ -1/2-1/2*3^(1/2)]
z0 = -1/2, -1/2, 2-3^(1/2), 2+3^(1/2)
即 的稳定点有两个
因为函数 在有界闭集 上连续,必有最大值和最小值,而求得的稳定点又恰是两个,所以它们一个是最大点,另一个是最小,其最大
最小值为。(x73)
x1=-1/2+1/2*3^(1/2);
x2=-1/2-1/2*3^(1/2);
y1=-1/2+1/2*3^(1/2);
y2=-1/2-1/2*3^(1/2);
z1=2-3^(1/2);
z2=2+3^(1/2);
f1=(x1^2+y1^2+z1^2)^(1/2)
f2=(x2^2+y2^2+z2^2)^(1/2)
f1 = 0.5829 ; f2 = 4.2024










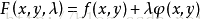
















 1182
1182

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










