机器学习入门（十四）：SVM——直观理解拉格朗日乘子法

上一篇，我们获得了线性可分 SVM 的目标函数：一个带约束条件的求极值问题。

而拉格朗日乘子法，恰恰是一种多元函数在变量受到条件约束时，求极值的方法。正好可以用来解决 SVM 的目标函数最优化。

我们在此不做严格的拉格朗日乘数法正确性的数学证明，而是以最简单的函数形式为例，从直观带大家来领略整个方法的每一个步骤。

换句话说，本文是帮我们积累一些对于“为什么将目标函数转化成拉格朗日函数再最优化是可行的”这件事的感性认识。

可视化函数及其约束条件

我们用二元函数——也就是自变量为2维的函数——来做个例子（为了看着更习惯一点，我们直接用 x、y 作为自变量的两个维度）。

（被约束的）函数

我们之前有过可视化函数本身的经验。此处我们先要可视化一个二元函数 f(x,y)。

用一个大家熟悉的表达方式：z=f(x,y) 。这就涉及了3个变量：x、y 和 z。

如果在三维直角坐标系中将 f(x,y) 做出图来——把 f(x,y) “画出图来”——会是一个三维空间的曲面——这样一个函数实际上表达了 x、y、z 三者之间的关系。

比如下面几幅图，分别对应不同的 f(x,y)：

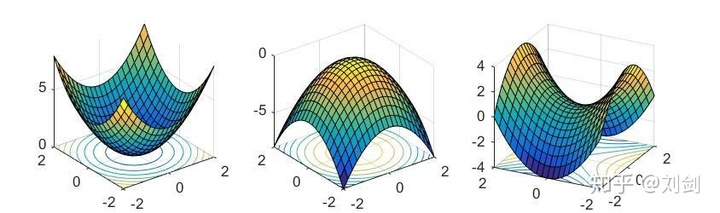
图 1

（函数的）约束条件

函数 f(x,y) 的约束条件为：g(x,y)=0。

g(x,y)=0 又可以写成：y=h(x) 的形式——它所表达的是 x 与 y 两者之间的相互关系！

y=h(x)，如果在二维直角坐标中作图，形状应该是一条曲线。

注意：直线也属于广义的曲线；平面也属于曲面。我们说的曲线是包括直线的，曲面则包括平面。

约束条件对函数的约束

那么，一个二维图形对一个三维图形的约束从何体现呢？让我们这样做：

1. 在自己的头脑中建立一个三维直角坐标系，有 x 轴、y 轴、z 轴， 它们互相垂直。
2. f(x,y) 对应图形是三维坐标系里面的一个曲面——一个（可能是奇形怪状的）“体”的“外皮”。
3. 在 z=0 的平面上，把 y=h(x) 的图形（一条曲线）画出来。
4. 将第 3 步做出的那条曲线沿着平行 z 轴的方向平移，它平移过的轨迹也形成了一个曲面，这个曲面和 z=f(x,y) 形成的曲面会相交，交叠的部分是一条三维空间中的曲线。
5. 换个角度考虑，第 4 步形成的曲线，其实就是 g(x,y)=0 在 z=0 平面上形成的曲线，在 z=f(x,y) 形成的曲面上的投影。

一个例子

图2是一个将上面 1-5 步骤综合起来的实例：