本篇承接上一篇文章,主要讲解最大流问题的Ford-Fulkerson解法。可是说这是一种方法,而不是算法,因为它包含具有不同运行时间的几种实现。该方法依赖于三种重要思想:残留网络,增广路径和割。本文将会详细介绍这些内容,下一篇文章我们提供一种该方法的Java实现。
在介绍着三种概念之前,我们先简单介绍下Ford-Fulkerson方法的基本思想。首先需要了解的是Ford-Fulkerson是一种迭代的方法。开始时,对所有的u,v属于V,f(u,v)=0(这里f(u,v)代表u到v的边当前流量),即初始状态时流的值为0。在每次迭代中,可以通过寻找一个“增广路径”来增加流值。增广路径可以看做是从源点s到汇点t之间的一条路径,沿该路径可以压入更多的流,从而增加流的值。反复进行这一过程,直到增广路径都被找出为止。
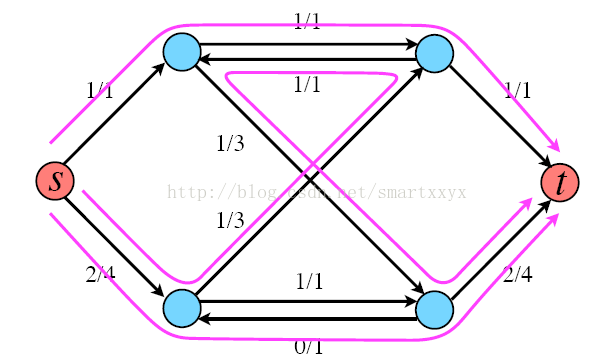
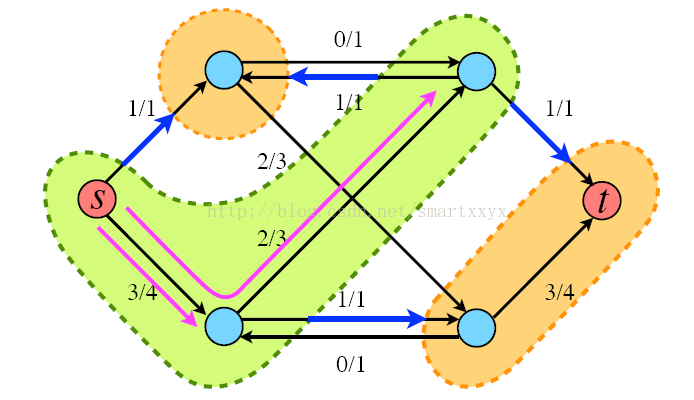
举个例子来说明下,如图所示,每条红线就代表了一条增广路径,当前s到t的流量为3。
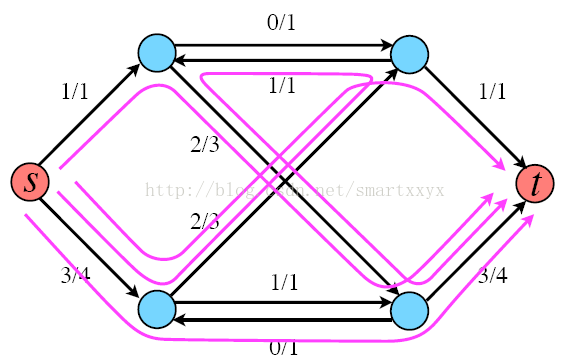
当然这并不是该网络的最大流,根据寻找增广路径的算法我们其实还可以继续寻找增广路径,最终的最大流网络如下图所示,最大流为4。
接下来我们就介绍如何寻找增广路径。在介绍增广路径之前,我们首先需要介绍残留网络的概念。
一、残留网络
顾名思义,残留网络是指给定网络和一个流,其对应还可以容纳的流组成的网络。具体说来,就是假定一个网络G=(V,E),其源点s,汇点t。设f为G中的一个流,对应顶点u到顶点v的流。在不超过C(u,v)的条件下(C代表边容量),从u到v之间可以压入的额外网络流量,就是边(u,v)的残余容量(residual capacity),定义如下:
r(u,v)=c(u,v)-f(u,v)
举个例子,假设(u,v)当前流量为3/4,那么就是说c(u,v)=4,f(u,v)=3,那么r(u,v)=1。
我们知道,在网络流中还有这么一条规律。从u到v已经有了3个单位流量,那么从反方向上看,也就是从v到u就有了3个单位的残留网络,这时r(v,u)=3。可以这样理解,从u到v有3个单位流量,那么从v到u就有了将这3个单位流量的压回去的能力。
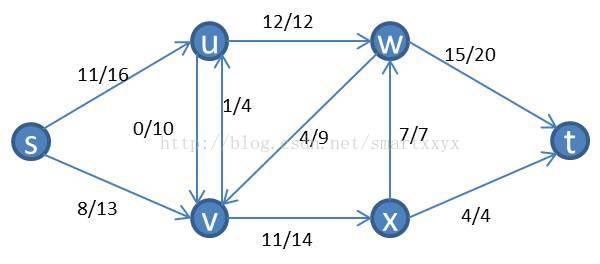
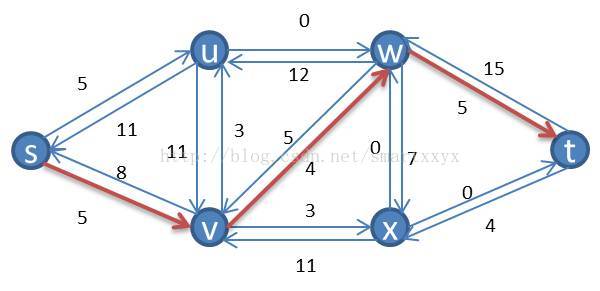
我们来具体看一个例子,如下图所示一个流网络
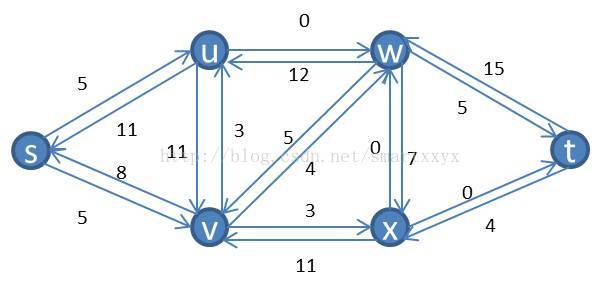
其对应的残留网络为:
二、增广路径
在了解了残留网络后,我们来介绍增广路径。已知一个流网络G和流f,增广路径p是其残留网络Gf中从s到t的一条简单路径。形象的理解为从s到t存在一条不违反边容量的路径,向这条路径压入流量,可以增加整个网络的流值。上面的残留网络中,存在这样一条增广路径:
其可以压入4个单位的流量,压入后,我们得到一个新的流网络,其流量比原来的流网络要多4。这时我们继续在新的流网络上用同样的方法寻找增广路径,直到找不到为止。这时我们就得到了一个最大的网络流。
三、流网络的割
上面仅仅是介绍了方法,可是怎么证明当无法再寻找到增广路径时,就证明当前网络是最大流网络呢?这就需要用到最大流最小割定理。
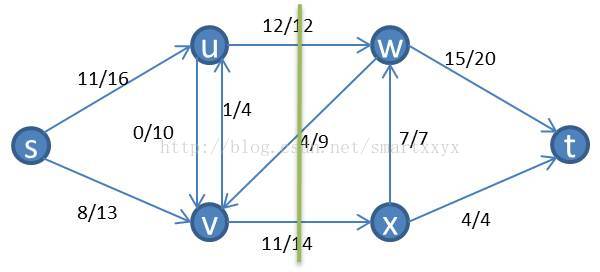
首先介绍下,割的概念。流网络G(V,E)的割(S,T)将V划分为S和T=V-S两部分,使得s属于S,t属于T。割(S,T)的容量是指从集合S到集合T的所有边(有方向)的容量之和(不算反方向的,必须是S-àT)。如果f是一个流,则穿过割(S,T)的净流量被定义为f(S,T)(包括反向的,SàT的为正值,T—>S的负值)。将上面举的例子继续拿来,随便画一个割,如下图所示:
割的容量就是c(u,w)+c(v,x)=26
当前流网络的穿过割的净流量为f(u,w)+f(v,x)-f(w,v)=12+11-4=19
显然,我们有对任意一个割,穿过该割的净流量上界就是该割的容量,即不可能超过割的容量。所以网络的最大流必然无法超过网络的最小割。
可是,这跟残留网络上的增广路径有什么关系呢?
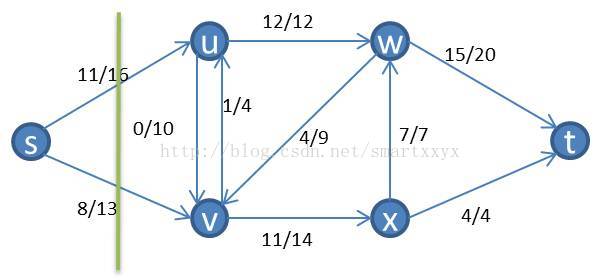
首先,我们必须了解一个特性,根据上一篇文章中讲到的最大流问题的线性规划表示时,提到,流网络的流量守恒的原则,根据这个原则我们可以知道,对网络的任意割,其净流量的都是相等的。具体证明是不难的,可以通过下图形象的理解下,
和上面的割相比,集合S中少了u和v,从源点s到集合T的净流量都流向了u和v,而在上一个割图中,集合S到集合T的流量是等于u和v到集合T的净流量的。其中w也有流流向了u和v,而这部分流无法流向源点s,因为没有路径,所以最后这部分流量加上s到u和v的流量,在u和v之间无论如何互相传递流,最终都要流向集合T,所以这个流量值是等于s流向u和v的值的。将s比喻成一个水龙头,u和v流向别处的水流,都是来自s的,其自身不可能创造水流。所以任意割的净流量都是相等的。
万事俱备,现在来证明当残留网络Gf中不包含增广路径时,f是G的最大流。
假设Gf中不包含增广路径,即Gf不包含从s到v的路径,定义S={v:Gf中从s到v存在一条通路},也就是Gf中s能够有通路到达的点的集合,显然这个集合不包括t,因为s到t没有通路。这时,我们令T=V-S。那么(S,T)就是一个割。如下图所示:
那么,对于顶点u属于S,v属于T,有f(u,v)=c(u,v)。否则(u,v)就存在残余流量,因而s到u加上u到v就构成了一条s到v的通路,所以v就必须属于S,矛盾。因此这时就表明当前流f是等于当前的割的容量的,因此f就是最大流。
接下来的文章我们再给出Java实现。
参考:《算法导论》《组合数学》







 本文详细阐述了Ford-Fulkerson最大流问题的解法,包括残留网络、增广路径和割的概念,并通过实例解释了寻找增广路径的过程。文章进一步解释了最大流最小割定理,证明了当残留网络中不再存在增广路径时,当前流即为最大流。最后,提供了Java实现的概述。
本文详细阐述了Ford-Fulkerson最大流问题的解法,包括残留网络、增广路径和割的概念,并通过实例解释了寻找增广路径的过程。文章进一步解释了最大流最小割定理,证明了当残留网络中不再存在增广路径时,当前流即为最大流。最后,提供了Java实现的概述。
















 22
22

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








