优化算法：牛顿法

我们在接触具体的机器学习算法前，其实很有必要对优化问题进行一些介绍。 
随着学习的深入，笔者越来越发现最优化方法的重要性，学习和工作中遇到的大多问题都可以建模成一种最优化模型进行求解，比如我们现在学习的机器学习算法，大部分的机器学习算法的本质都是建立优化模型，通过最优化方法对目标函数（或损失函数）进行优化，从而训练出最好的模型。
最常见的最优化方法有梯度下降法、牛顿法和拟牛顿法、共轭梯度方向法等。 
在大学课程中，数值分析是计算机或数学相关专业一门比较重要的一门课程，笔者也在大学时自学过相关课程，其介绍的诸多对理论的计算机实现方法，对现在的学习依然发挥着很大的作用。
当然优化算法只是数值分析课程中涉及一部分内容，这一节主要介绍和回顾牛顿法。

牛顿法

上节介绍的梯度下降法（最速下降法）只用到了目标函数的一阶导数，牛顿法是一种二阶优化算法，相对于梯度下降算法收敛速度更快。
首先，选择一个接近函数$f(x)$零点的$x_0$，计算相应的$f(x_0)$ 和切线斜率$f ' (x_0)$。然后我们计算穿过点$(x_0, f(x_0))$ 并且斜率为$f '(x_0)$的直线和 $X$轴的交点的$x$坐标，也就是求如下方程的解：
$f(x_0)+f'(x_0)*(x-x_0)=0$
我们将新求得的点的$x$坐标命名为$x_1$，通常$x_1$会比$x_0$更接近方程$f(x) = 0$的解。因此我们现在可以利用$x_1$开始下一轮迭代。迭代公式可化简为如下所示：
$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$

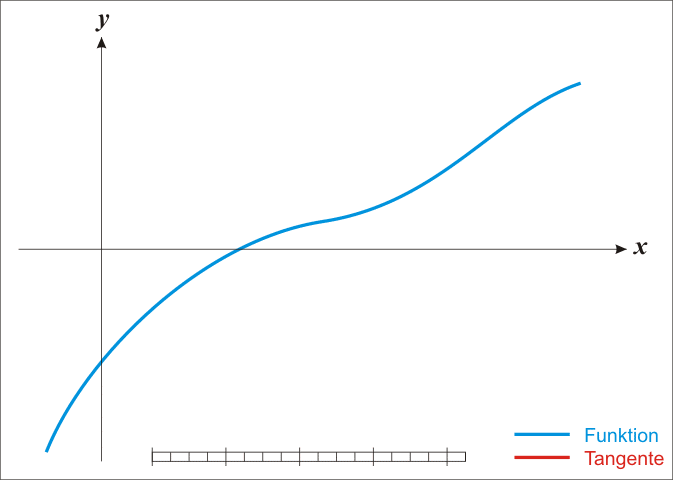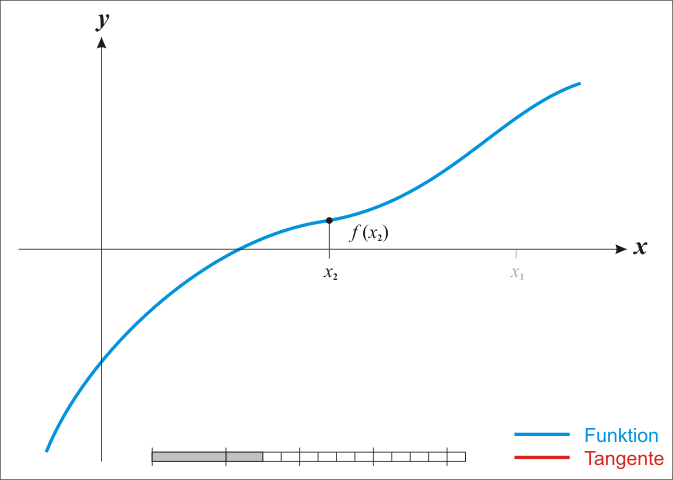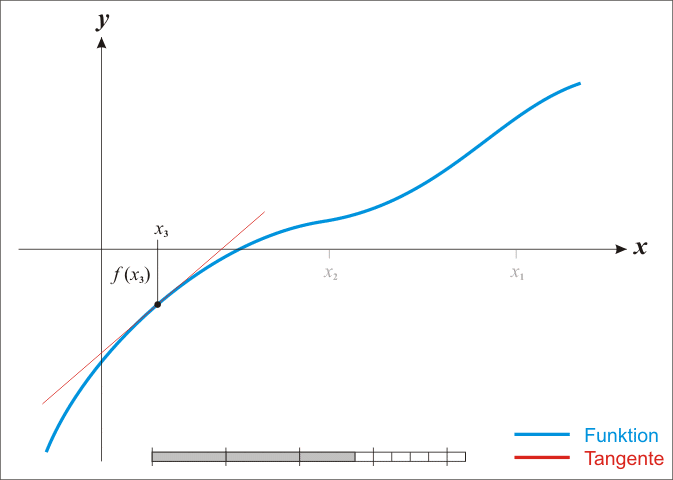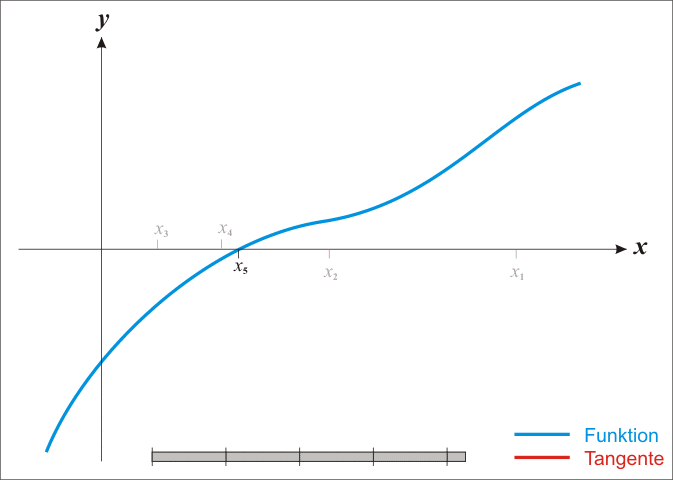
牛顿法是基于当前位置的切线来确定下一次的位置，所以牛顿法又被很形象地称为是”切线法”。牛顿法的搜索路径（二维情况）如下图所示：

缺点

牛顿法也有很大的缺点，就是每次计算都需要计算Hessian矩阵的逆，因此计算量较大。

拟牛顿法

拟牛顿法在一定程度上解决了牛顿法计算量大的问题。其本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。（在多变量的情况下，如果目标矩阵的Hessain矩阵非正定，牛顿法确定的搜索方向并不一定是目标函数下降的方向）
拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化，构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法，尤其对于困难的问题。另外，因为拟牛顿法不需要二阶导数的信息，所以有时比牛顿法更为有效。如今，优化软件中包含了大量的拟牛顿算法用来解决无约束，约束，和大规模的优化问题。

拟牛顿法的Matlab实现：

#函数名：quasi_Newton(f,x0,error), 
#参数：f:待求梯度函数   x0:初始点   error：允许误差 
#主程序： 
function A=quasi_Newton(f,x0,error) 
     [a,b]=size(x0); 
     G0=eye(b); 
     initial_gradient=gradient_my(f,x0,b); 
     norm0=0; 
     norm0=initial_gradient*initial_gradient'; 
     syms step_zzh; 
     A=[x0]; 
     search_direction=-initial_gradient; 
     x=x0+step_zzh*search_direction; 
     f_step=subs(f,findsym(f),x); 
     best_step=golden_search(f_step,-15,15); 
     x_1=x0+best_step*search_direction; 
     A=[A;x_1]; 
     k=1; 
while norm0>error 
     ox=x_1-x0; 
     og=gradient_my(f,x_1,b)-initial_gradient; 
     G1=G0+(ox'*ox)/(ox*og')-(G0*og'*og*G0)/(og*G0*og'); 
     if  k+1==b 
         new_direction=-gradient_my(f,x_1,b); 
     else 
         new_direction=-(G1*(gradient_my(f,x_1,b))')'; 
     end 
     x=x_1+step_zzh*new_direction; 
     f_step=subs(f,findsym(f),x); 
     best_step=golden_search(f_step,-15,15) 
     x_2=x_1+best_step*new_direction 
     A=[A;x_2]; 
     initial_gradient=gradient_my(f,x_1,b); 
     norm0=initial_gradient*initial_gradient'; 
     x0=x_1;x_1=x_2; 
     G0=G1; 
     k=k+1; 
end