漫步数学分析三十二——可微映射的连续性

对于单变量实值函数而言，$f:(a,b)\to R$在$x_0$处可微，那么

$$\begin{align*} \lim_{x\to x_0}(f(x)-f(x_0)) &=\lim_{x\to x_0}\left(\frac{f(x)-f(x_0)}{x-x_0}\right)\cdot(x-x_0)\\ &=f^\prime(x_0)\cdot\lim_{x\to x_0}(x-x_0)=f^\prime(x_0)\cdot0=0 \end{align*}$$

所以$\lim_{x\to x_0}(f(x)-f(x_0))=0$，这就意味着$f$在$x_0$处连续。

这些想法可以推广到更一般的情况：$f:A\subset R^n\to R^m$，从而引出下面的定理。

$\textbf{定理3}$ 假设$A\subset R^n$是开集且$f:A\to R^m$在$A$上可微，那么$f$是连续的。事实上，对于每个$x_0\in A$存在一个常数$M>0,\delta_0>0$使得$\Vert x-x_0\Vert<\delta_0$意味着$\Vert f(x)-f(x_0)\Vert\leq M\Vert x-x_0\Vert$。(这就是利普希茨(Lipschitz)性质)

前面我们讨论的都是实值函数的特殊情况，$f:R^n\to R$，函数$c:R\to R^m$也是重要的，这里的$c$表示$R^m$中的曲线或路径，这种情况下$Dc(t):R\to R^m$ 用向量

$$\begin{pmatrix} \frac{dc_1}{dt}\\ \cdot\\ \cdot\\ \cdot\\ \frac{dc_m}{dt} \end{pmatrix}$$

表示，其中$c(t)=(c_1(t),\ldots,c_m(t))$。这个向量用$c^\prime(t)$表示并称为曲线的切向量或速度向量，如果注意到$c^\prime(t)=\lim_{h\to 0}(c(t+h)-c(t))/h$并利用事实：$[c(t+h)-c(t)]/h$是近似曲线切线的一条弦，那么我们将看到$c^\prime(t)$应该表示精确的且向量(如图1)。 用移动的质点来说的话，$(c(t+h)-c(t))/h$ 是速度的近似，因为它是位移/时间，所以$c^\prime(t)$是瞬时速度。

严格来讲我们应该讲$c^\prime(t)$表示成列向量，因为矩阵$Dc(t)$矩阵是一个$3\times 1$矩阵。然而这样的话排版比较麻烦，所以我们以后写$c^\prime(t)$时表示行向量。

$\textbf{例1：}$证明$f:R\to R,x\mapsto|x|$是连续的但在0处不可微。

$\textbf{解：}$对于$x\geq0,f(x)=x$，对于$x<0,f(x)=-x$，所以$f$在$(0,\infty),(-\infty,0)$上是连续的。因为$\lim_{x\to 0}f(x)=0=f(0)$，那么$f$在0处也是连续的，所以$f$在所有点处均连续。最后，$f$在0处不可微，因为如果可微的话，那么

$$\lim_{x\to0}\frac{f(x)-f(0)}{x-0}=\lim_{x\to 0}\frac{f(x)}{x}$$

将会存在，但是当$x>0$时，$f(x)/x$为+1，当$x<0$时，$f(x)/x$为-1，从而极限不可能存在。

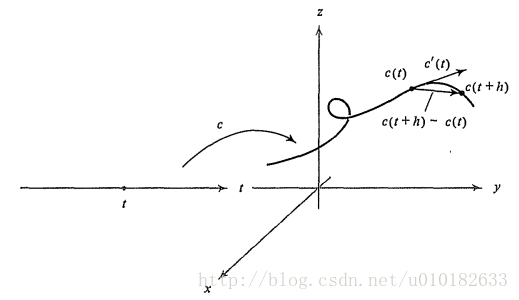
图1

$\textbf{例2：}$函数的导数一定连续吗？

$\textbf{解：}$答案为否，但是实例不是很明显。也许最简单的例子是

$$f(x)= \begin{cases} x^2\sin(\frac{1}{x}),&x\neq 0\\ 0,&x=0 \end{cases}$$

如图2所示。

为了证明零处不可微，我们需要说明

$$\text{当}x\to 0\text{时},\frac{f(x)}{x}\to 0$$

事实上，当$x\to 0$时$|f(x)/x|=|x\sin(1/x)|\leq|x|\to 0$，从而$f^\prime(0)$存在且是零，故$f$在0处可微。接下来，根据基本微积分内容

$$f^\prime(x)=2x\sin\left(\frac{1}{x}\right)-\cos\left(\frac{1}{x}\right),\quad x\neq 0$$

当$x\to 0$时第一项$\to 0$但是第二项在$+1,-1$之间震荡，所以$\lim_{x\to 0}f^\prime(x)$不存在，从而$f^\prime$存在但是不连续。

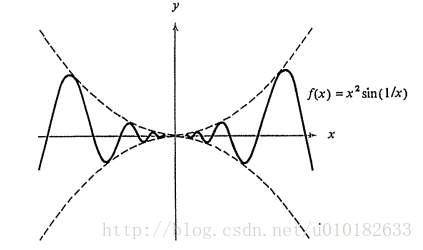
图2

$\textbf{例3：}$令 $c(t)=(t^2,t,\sin t)$，找出 $c(t)$在点 $c(0)=(0,0,0)$处的切向量。

$\textbf{解：}$$c^\prime(t)=(2t,1,\cos t)$，令$t=0,c^\prime(0)=(0,1,1)$，即$c(t)$在点$(0,0,0)$处的切向量。