无监督聚类算法该如何评价

       学过机器学习的小伙伴应该都很清楚：几乎所有的机器学习理论与实战教材里面都有非常详细的理论化的有监督分类学习算法的评价指标。例如：正确率、召回率、精准率、ROC曲线、AUC曲线。但是几乎没有任何教材上有明确的关于无监督聚类算法的评价指标！

       那么学术界到底有没有成熟公认的关于无监督聚类算法的评价指标呢？本文就是为了解决大家的这个疑惑而写的，并且事先明确的告诉大家，关于无监督聚类算法结果好坏的评价指标不仅有，而且还挺多的。接下来我会一一详述！

1、有类标的情况

       既然聚类是把一个包含若干文档的文档集合分成若干类，像上图如果聚类算法应该把文档集合分成3类，而不是2类或者5类，这就设计到一个如何评价聚类结果的问题。下面介绍几种聚类算法的评价指标，看下图：

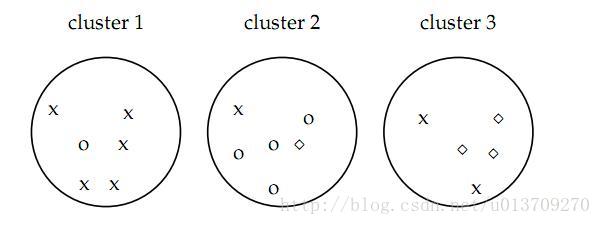
      如图，认为x代表一类文档，o代表一类文档，方框代表一类文档，完美的聚类显然是应该把各种不同的图形放入一类，事实上我们很难找到完美的聚类方法，各种方法在实际中难免有偏差，所以我们才需要对聚类算法进行评价看我们采用的方法是不是好的算法。

1.1 Purity方法

       purity方法是极为简单的一种聚类评价方法，只需计算正确聚类的文档数占总文档数的比例：

$$purity(\Omega , C)=\frac{1}{N}\sum_k \max_j|\omega_k \cap c_j|$$

       其中$Ω = \{ ω_1, ω_2, . . . , ω_k\}$ 是聚类的集合$ω_k$表示第k个聚类的集合。$C = \{c_1, c_2, . . . , c_j\}$是文档集合，$c_j$表示第j个文档。N表示文档总数。

如上图的:

$$purity = ( 3+ 4 + 5) / 17 = 0.71$$

其中第一类正确的有5个，第二个4个，第三个3个，总文档数17。

       purity方法的优势是方便计算，值在0～1之间，完全错误的聚类方法值为0，完全正确的方法值为1。同时，purity方法的缺点也很明显它无法对退化的聚类方法给出正确的评价，设想如果聚类算法把每篇文档单独聚成一类，那么算法认为所有文档都被正确分类，那么purity值为1！而这显然不是想要的结果。

1.2 RI方法(Rand index兰德指数)

      RI方法实际上这是一种用排列组合原理来对聚类进行评价的手段，公式如下：

$$RI=\frac{TP+FP}{TP+FP+TN+FN}$$

      其中TP是指被聚在一类的两个文档被正确分类了，TN是只不应该被聚在一类的两个文档被正确分开了，FP只不应该放在一类的文档被错误的放在了一类，FN只不应该分开的文档被错误的分开了。对上图

$$TP＋FP ＝ C(2,6) + C(2,6) + C(2,5) = 15 + 15 + 10 = 40$$

其中$C(n,m)$是指在m中任选n个的组合数。

$$TP = C(2,5) + C(2,4) + C(2,3) + C(2,2) = 20$$

$$FP = 40 - 20 = 20$$

相似的方法可以计算出:

$$TN = 72\qquad FN = 24$$

所以:

$$RI ＝ ( 20 + 72) / ( 20 + 20 + 72 +24) = 0.68$$

1.3 F值方法

这是基于上述RI方法衍生出的一个方法，

$$P=\frac{TP}{TP+FP}$$

$$R=\frac{TP}{TP+FN}$$

$$F_\beta=\frac{(\beta^2+1)PR}{\beta^2P+R}$$

       RI方法有个特点就是把准确率和召回率看得同等重要，事实上有时候我们可能需要某一特性更多一点，这时候就适合F值方法

2、无类标的情况

       对于无类标的情况，没有唯一的评价指标。对于数据 凸分布 的情况我们只能通过 类内聚合度、类间低耦合 的原则来作为指导思想，如下如：

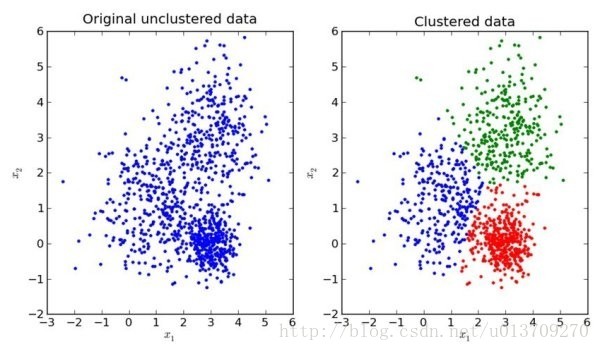
       当然，有这些还不够，对于如下图所示的数据在N维空间中的不是 凸分布 的情况下，此时我们就需要采用另外的一些评价指标。典型的无监督聚类算法也很多，例如基于局部密度的LOF算法，DBSCAN算法等，在此种情况下的聚类效果就非常的优秀。

2.1 Compactness(紧密性)(CP)

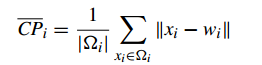
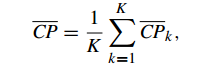
       CP计算每一个类各点到聚类中心的平均距离CP越低意味着类内聚类距离越近。著名的 K-Means 聚类算法就是基于此思想提出的。

缺点：没有考虑类间效果

2.2 Separation(间隔性)(SP)

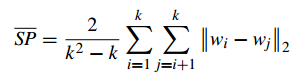
SP计算 各聚类中心两两之间平均距离，SP越高意味类间聚类距离越远

缺点：没有考虑类内效果

2.3 Davies-Bouldin Index(戴维森堡丁指数)(分类适确性指标)(DB)(DBI)

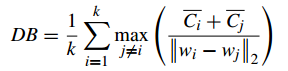
DB计算 任意两类别的类内距离平均距离(CP)之和除以两聚类中心距离求最大值。DB越小意味着类内距离越小 同时类间距离越大

缺点：因使用欧式距离 所以对于环状分布 聚类评测很差

2.4 Dunn Validity Index (邓恩指数)(DVI)

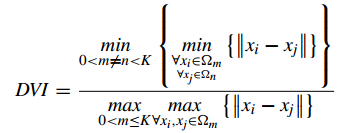
DVI计算 任意两个簇元素的最短距离(类间)除以任意簇中的最大距离(类内)。 DVI越大意味着类间距离越大 同时类内距离越小

缺点：对离散点的聚类测评很高、对环状分布测评效果差

对机器学习，人工智能感兴趣的小伙伴，请关注我的公众号：

参考文献：

1. Yanchi Liu, Zhongmou Li, Hui Xiong, Xuedong Gao, Junjie Wu:
   Understanding of Internal Clustering Validation Measures. 911-916

2. http://blog.csdn.net/u012102306/article/details/52423074