图的割点算法vs图的割边算法

图的割点

在一个无向连通图中，如果删除某个顶点后，图不再连通（即任意两点之间不能相互到达），我们称这样的顶点为割点（或者称割顶）。

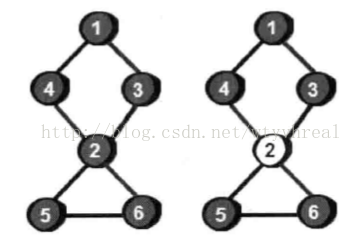
上图中的2号顶点就是割点，因为删除2号后，4,5不通，1,6也不通。

很容易想到的方法是：依次删除每一个顶点，然后用dfs或者bfs来检查图是否依然连通。如果删除某个顶点后，导致图不再连通，那么刚才删除的顶点就是割点。

这种方法的时间复杂度是O(N(N+M))。

下面寻找复杂度低的方法来解决。

dfs遍历上图后，如下图，圆圈中数字是顶点编号，圆圈右上角的数表示这个顶点在遍历时是第几个被访问到的，叫做“时间戳”。