背包问题——“完全背包”最优方案总数分析及实现

 -----Edit by ZhuSenlin HDU

        本人博文《背包问题——“完全背包”详解及实现（包含背包具体物品的求解）》中已详细谈过完全背包问题，同时在博文《背包问题——“01背包”最优方案总数分析及实现》中也总结过01背包的最优方案总数的实现。这里我们模仿01背包最优方案总数方法给出完全背包的最优方案求解方法。

   

        重写完全背包的动态规划的状态及状态方程：

        完全背包是在N种物品中选取若干件（同一种物品可多次选取）放在空间为V的背包里，每种物品的体积为C₁，C₂，…，C_n，与之相对应的价值为W₁,W₂，…，W_n.求解怎么装物品可使背包里物品总价值最大。

   

        设物品种类为N，背包容量为V，每种物品的体积为C[i]，价值为W[i]。

子问题定义：F[i][j]表示前i种物品中选取若干件物品放入剩余空间为j的背包中所能得到的最大价值。

       状态方程为：

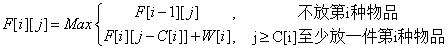                                     (2-2)

 

         在文章《背包问题——“01背包”最优方案总数分析及实现》中曾定义G[i][j]代表F[i][j]的方案总数。这里我们也做相同的定义，那么最终的结果应该为G[N][V]。

   

        由01背包转变到完全背包后G[i][j]该怎么求？

        对于01背包来说，G[i][j]求法如下（摘自：《背包问题——“01背包”最优方案总数分析及实现》）：

        如果F[i][j]=F[i-1][j]且F[i][j]!=F[i-1][j-C[i]]+W[i]说明在状态[i][j]时只有前i-1件物品的放入才会使价值最大，所以第i件物品不放入，那么到状态[i][j]的方案数应该等于[i-1][j]状态的方案数即G[i][j]=G[i-1][j]；

        如果F[i][j]=F[i-1][j-C[i]]+W[i] 且F[i][j]!=F[i-1][j]说明在状态[i][j]时只有第i件物品的加入才会使总价值最大，那么方案数应该等于[i-1][j-C[i]]的方案数，即G[i][j]=G[i-1][j-C[i]]；

        如果F[i][j]=F[i-1][j-C[i]]+W[i] 且F[i][j]=F[i-1][j]则说明即可以通过状态[i-1][j]在不加入第i件物品情况下到达状态[i][j]，又可以通过状态[i-1][j-C[i]]在加入第i件物品的情况下到达状态[i][j]，并且这两种情况都使得价值最大且这两种情况是互斥的，所以方案总数为G[i][j]=G[i-1][j-C[i]]+ G[i-1][j]。

 

        对于完全背包，我们也可以根据其状态方程来进行条件判断：

        如果F[i][j] = F[i-1][j]且F[i][j] != F[i][j-C[i]]+W[i]，说明背包总不存在第i种物品，也就是说背包种物品仍由前i-1种物品组成，那么应该有G[i][j] = G[i-1][j]；

        如果F[i][j] = F[i][j-C[i]]+W[i]且F[i][j] != F[i-1][j]，则说明背包中必定存在第i种物品使背包达到[i][j]状态的最大值，G[i][j] = G[i][j-C[i]]；

        如果F[i][j] = F[i][j-C[i]]+W[i]且F[i][j] = F[i-1][j]，则说明背包中存在i与不存在i都可以达到最大值，那么这个方案数应该由两者叠加，因为这两种情况是互斥的，即G[i][j] = G[i-1][j]+G[i][j-C[i]]。

        伪代码如下（注意和01背包情况的区分）：

  F[0][] ← 0

  F[][0] ← 0

  G[][ ] ← 1

  for i ← 1 to N

      do for j ← 1 to V

          F[i][j] ← F[i-1][j]

          G[i][j] ← G[i-1][j]

          if (j >= C[i])

              if (F[i][j] < F[i][j-C[i]]+W[i])

                  then F[i][j] ← F[i][j-C[i]]+W[i]

                       G[i][j] ← G[i][j-C[i]]

              else if (F[i][j] = F[i][j-C[i]]+W[i])

                  then G[i][j] ← G[i-1][j]+G[i][j-C[i]]

  return F[N][V] and G[N][V]

同样，上述方法在保存状态F[][]及G[][]时需要O(NV)的空间复杂度，下面我们对空间复制度进行优化。

 

压缩空间复杂度为O(V)

F[i][j]与G[i][j]只分别与F[i-1][]和G[i-1][]的状态有关，所以我们可以用两个一维数组F[]和G[]来替换二维数组F[][]和G[][]。

直接给出伪代码：

  F[] ← 0

  G[] ← 1

  for i ← 1 to N

      do for j ← C[i] to V

          if (F[j] < F[j-C[i]]+W[i])

              then F[j] ← F[j-C[i]]+W[i]

                   G[j] ← G[j-C[i]]

          else if (F[j] = F[j-C[i]]+W[i])

              then G[j] ← G[j]+G[j-C[i]]

  return F[V] and G[V]

和01背包的最优方案总数相比上述伪代码只是调换了一下C[i]与V的遍历顺序，具体思想请看博文《背包问题——“完全背包”详解及实现（包含背包具体物品的求解）》

 

下面对数据表给出以上两种不同空间复杂度的详细代码：

完全背包数据表（背包容量为10）

物品号i	1	2	3
体积C	2	2	2
价值W	5	5	5

因为完全背包的方案一般较多，这里只列举3种物品，方便大家验证。

 

#include <iostream>
#include <cstring>
#include "CreateArray.h"	//该头文件用于动态创建和销毁二维数组，读者自己实现

using namespace std;

//时间复杂度O(VN),空间复杂度为O(VN)

int Package02Optimal(int Weight[], int Value[], int nLen, int nCapacity)
{
	int** MaxValueTable = NULL;
	int** OptimalTable = NULL;
	CreateTwoDimArray(MaxValueTable,nLen+1,nCapacity+1);	//创建最大价值表
	CreateTwoDimArray(OptimalTable,nLen+1,nCapacity+1);	//创建最优方案总数表

	//initiallize all OptimalTable[][] with 1
	for(int i = 0; i <= nLen; i++)
		for(int j = 0; j <= nCapacity; j++)
			OptimalTable[i][j] = 1;
	
	for(int i = 1; i <= nLen; i++)
	{
		for(int j = 1; j <= nCapacity; j++)
		{
			MaxValueTable[i][j] = MaxValueTable[i-1][j];
			OptimalTable[i][j] = OptimalTable[i-1][j];
			if(j >= Weight[i-1])
			{
			   	if(MaxValueTable[i][j] < MaxValueTable[i][j-Weight[i-1]]+Value[i-1])
				{
					MaxValueTable[i][j] = MaxValueTable[i][j-Weight[i-1]]+Value[i-1];
					OptimalTable[i][j] = OptimalTable[i][j-Weight[i-1]];
				}
				else if(MaxValueTable[i][j] == (MaxValueTable[i][j-Weight[i-1]]+Value[i-1]))
				{
					OptimalTable[i][j] = OptimalTable[i-1][j]+OptimalTable[i][j-Weight[i-1]];
				}
			}
		}
	}

	cout << endl << "OptimalCount:" << OptimalTable[nLen][nCapacity] << endl;

	int nRet = MaxValueTable[nLen][nCapacity];
	DestroyTwoDimArray(MaxValueTable,nLen+1);	//销毁最大价值表，防止内存泄露
	DestroyTwoDimArray(OptimalTable,nLen+1);	//销毁最优方案表，防止内存泄露
	return nRet;
}

//时间复杂度O(VN),空间复杂度为O(V)

int Package02Optimal_Compress(int Weight[], int Value[], int nLen, int nCapacity)
{
	int * MaxValueTable = new int [nCapacity+1];
	memset(MaxValueTable,0,(nCapacity+1)*sizeof(int));

	//initiallize all OptimalTable[] with 1
	int* OptimalTable = new int[nCapacity+1];
	for(int i = 0; i <= nCapacity; i++)
		OptimalTable[i] = 1;
	
	for(int i = 0; i < nLen; i++)
	{
		for(int j = Weight[i]; j <= nCapacity; j++)
		{
			if(MaxValueTable[j] < MaxValueTable[j-Weight[i]]+Value[i])
			{
				MaxValueTable[j] = MaxValueTable[j-Weight[i]]+Value[i];
				OptimalTable[j] = OptimalTable[j-Weight[i]];
			}
			else if(MaxValueTable[j] == MaxValueTable[j-Weight[i]]+Value[i])
				OptimalTable[j] = OptimalTable[j-Weight[i]]+OptimalTable[j];
		}
	}

	cout << endl << "OptimalCount:" << OptimalTable[nCapacity] << endl;

	int nRet = MaxValueTable[nCapacity];
	delete [] OptimalTable;
	delete [] MaxValueTable;
	return nRet;
}

//测试代码

int main()
{
	//int Weight[] = {3,2,5,1,6,4};
	//int Value[] =  {6,5,10,2,16,8};
	int Weight[] = {2,2,2};
	int Value[] =  {5,5,5};
	int nCapacity = 10;
	cout << "MaxValue:" << Package02Optimal(Weight,Value,sizeof(Weight)/sizeof(int),nCapacity) << endl;
	cout << "MaxValue:" << Package02Optimal_Compress(Weight,Value,sizeof(Weight)/sizeof(int),nCapacity) << endl;
	return 0;
}

以上部分内容参考《背包九讲》