机器学习基础(林軒田)笔记之六
Theory of Generalization(机器学习的一般化)
一.Restriction of Break Point(断点的限制)
首先,回顾上一节课中所讲述的成长函数和断点机制。
成长函数:假设空间在N个样本点上能够产生的最大二分类的数量;
断点机制:不能满足完全分类的样本点个数,完全二分类可以有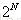

下面假设分类的最小断点数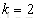
下图中为N=1,2的时的情况;

下面几个图为N=3时的情况;
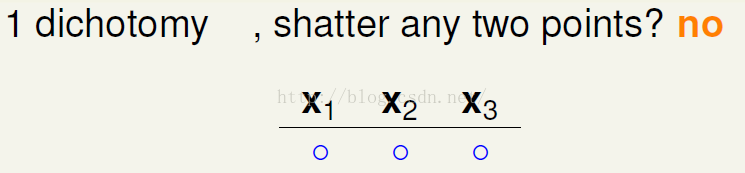


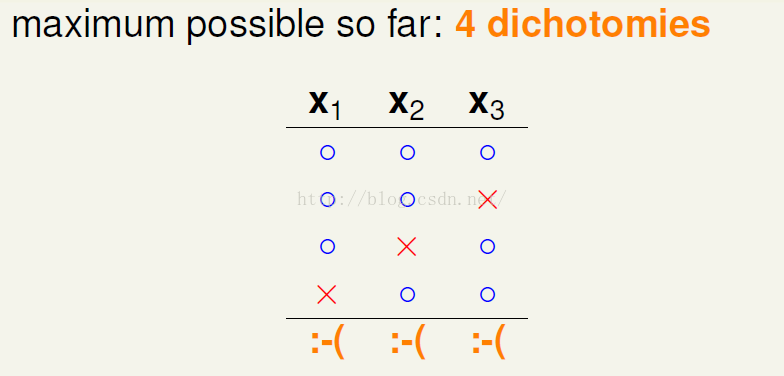
由上面三图可知当为不重复的三种二分类情况时,符合题设的不存在两个点完全二分的情况,下图为第四种不重复的二分类情况,此时x2和x3出现完全二分情况;

变换二分类的方式得到第四种不存在任意两个点完全二分的情况;

第五种二分方式会造成两个点完全二分,不符而要求;
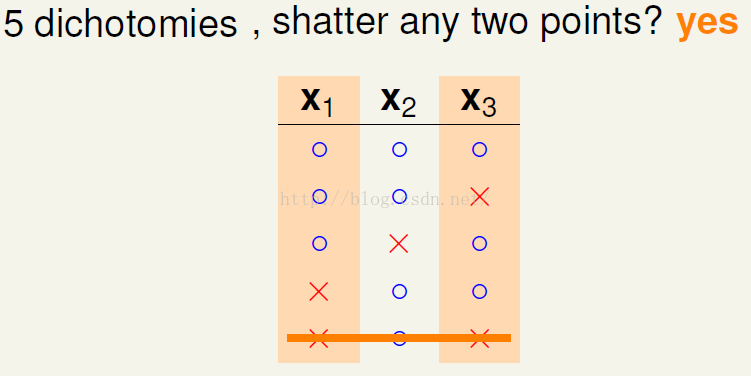
结论,最多存在四中划分方式满足任意两个点不存在完全二分类的情况。
得出猜想:

二.Bounding Function: Basic Cases(上限函数的基本情况)
下面我们将上面的猜想定义为一个上限函数: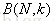 ,表示在断点为k时成长函数
,表示在断点为k时成长函数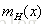 的最大值。
的最大值。
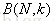 ,表示在断点为k时成长函数
,表示在断点为k时成长函数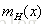 的最大值。
的最大值。
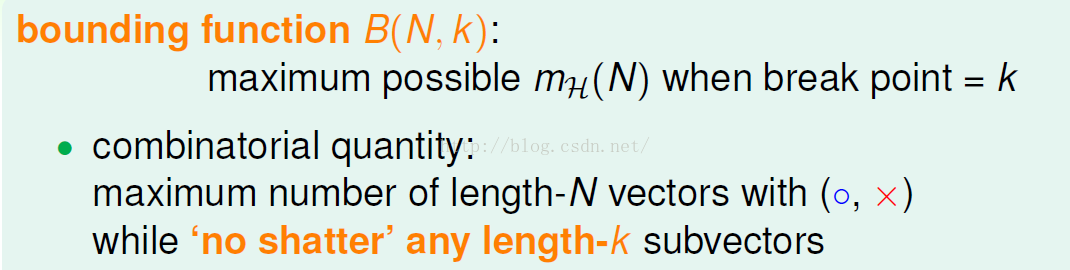
通俗的讲,就是对维度为N的向量进行二分类,在保证其中任意k个特征不能完全二分的分类种类的最大值。
例如:

结果:




三.Bounding Function: Inductive Cases(边界函数的归纳情况)
本节课我们完成上节课中表格的剩余部分。
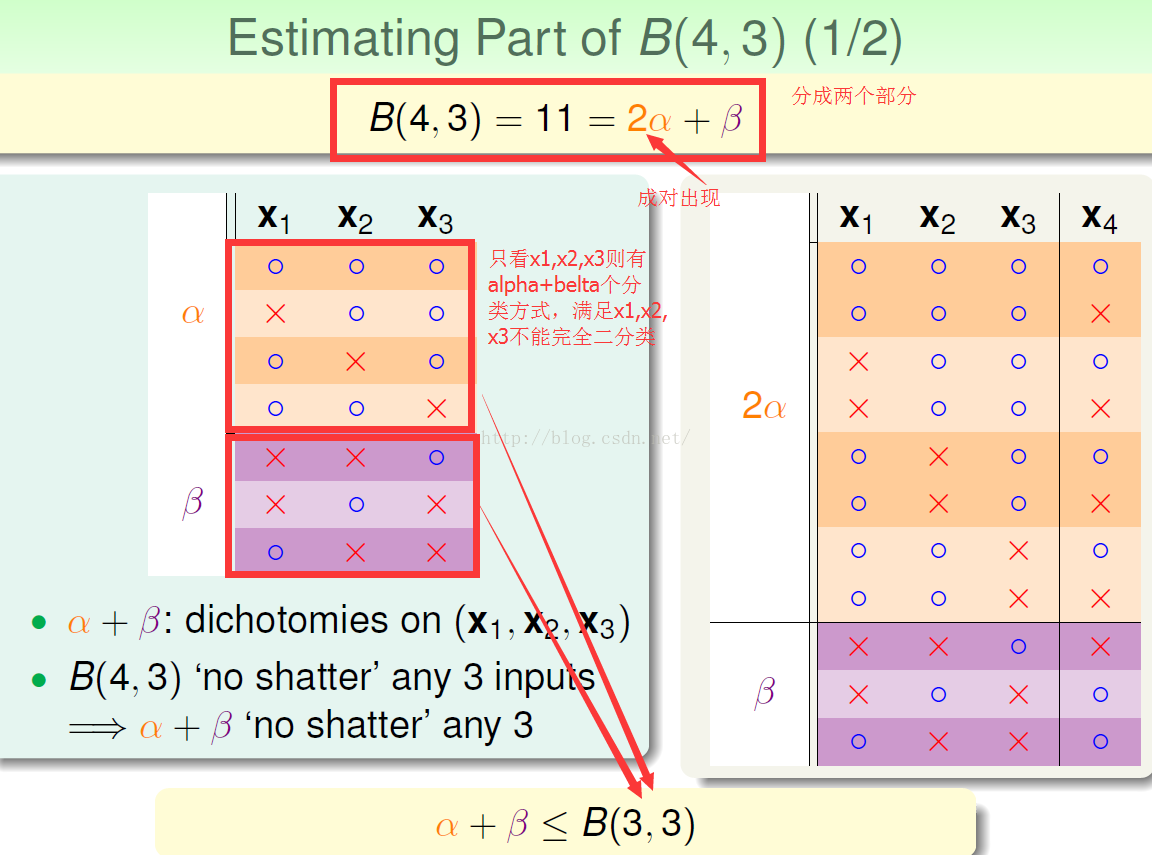
猜想B(4,3)是否与B(3,?)有关:

写一个计算机程序求B(4,3),得:
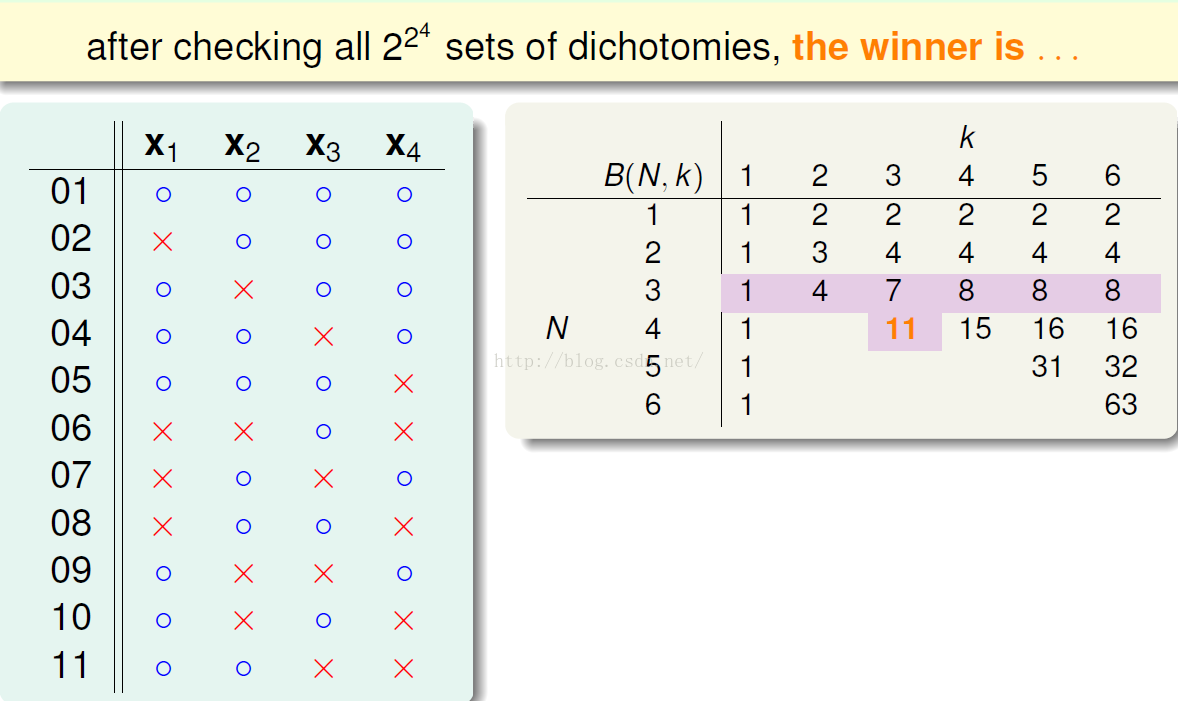
整理得到:
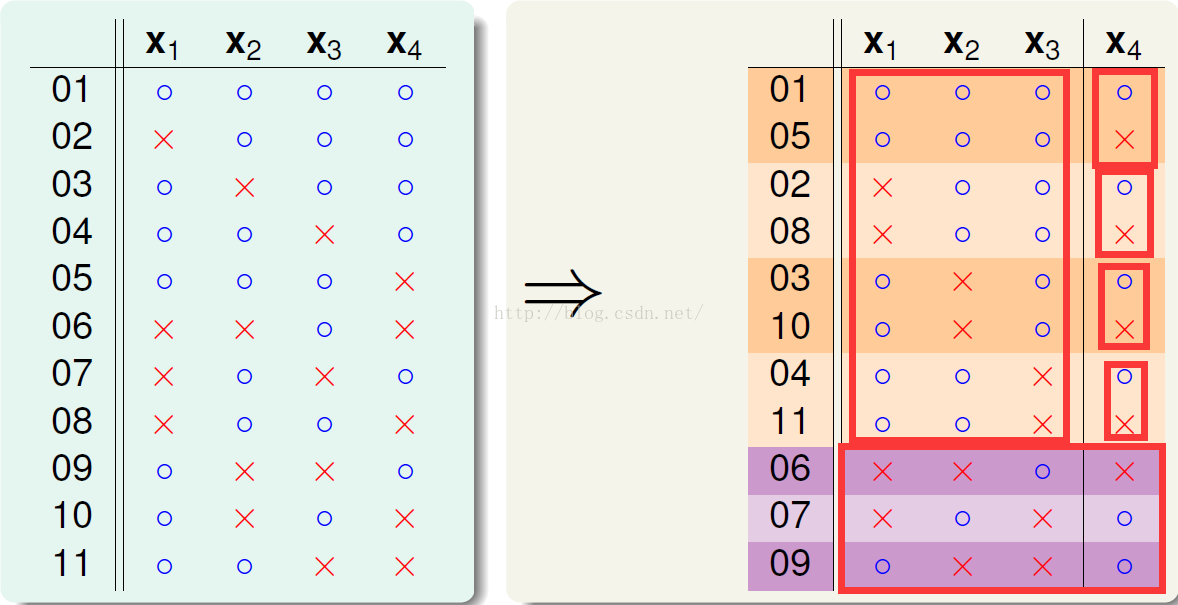
进一步:
进一步,忽略x4,只看橘色的部分:
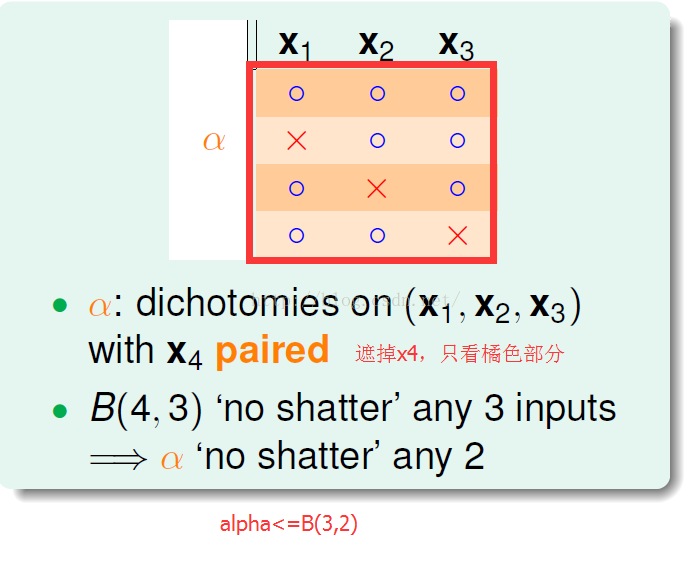
推论:

由此,我们可以证明上限函数的上限:
证明如下:
已知,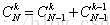
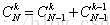
当k=1时上式显然成立 ;
;
 ;
;
当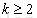 时,假设
时,假设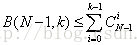 ,
,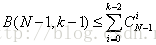 成立,则:
成立,则:
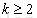 时,假设
时,假设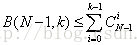 ,
,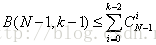 成立,则:
成立,则:
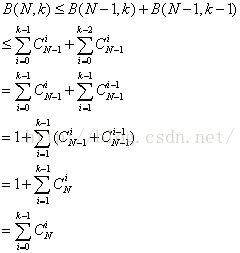
得证。
综上我们可以得出,成长函数会被上限函数bound,上限函数会被上限函数边界bound,上限的上限会被某个多项式bound。
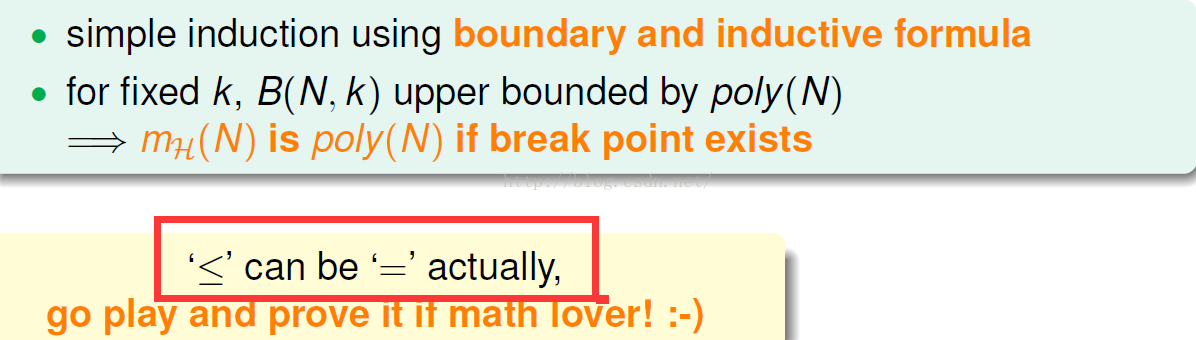
例:

四.A Pictorial Proof(形象化的证明)
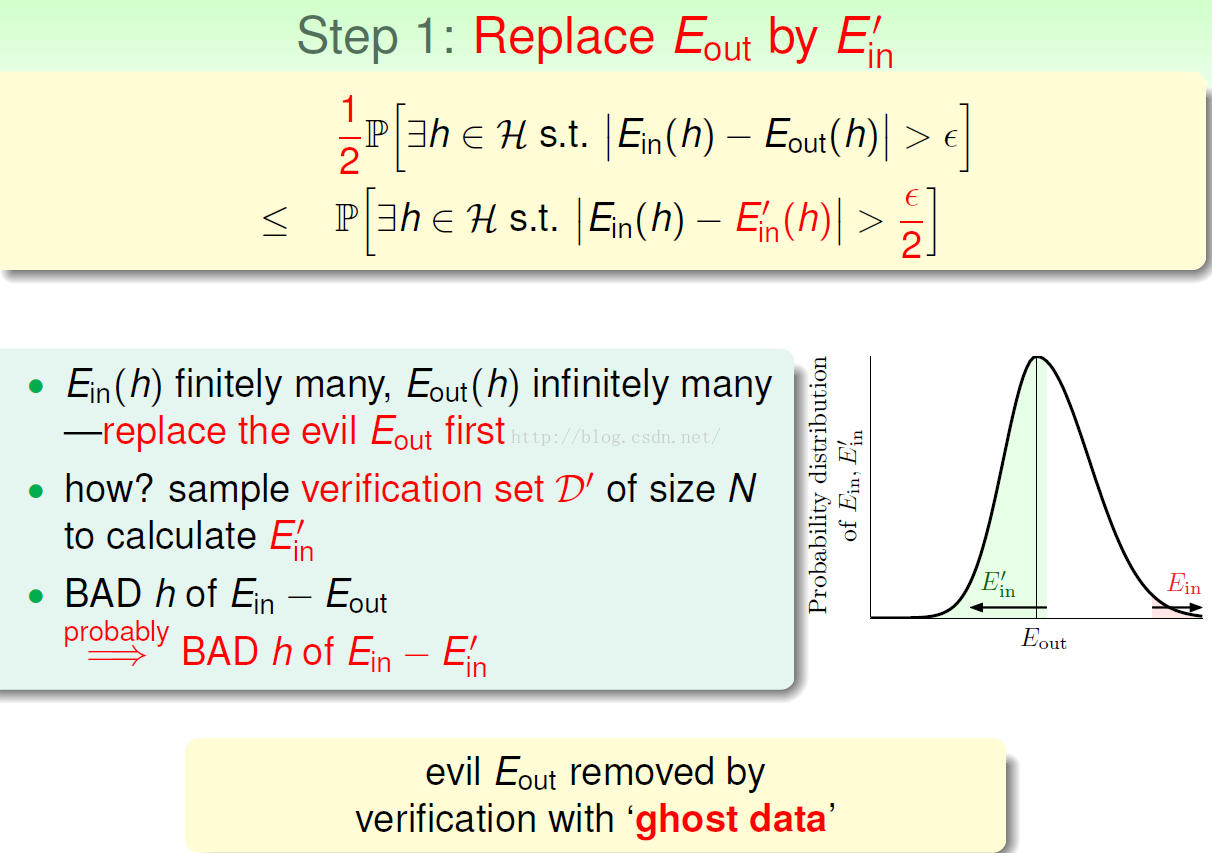
基于第三节,我们得到成长函数的上界,那么我们将成长函数直接代入霍夫丁不等式中就能证明机器学习是可行的,但是实际的结果与其稍微有些差别,见下图(证明难度较大,不予以证明):
下面介绍这些微妙的差别是如何发生的:

























 840
840











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








