Neural Networks and Deep Learning学习笔记ch2 - 反向传播

---

在上一节中简单介绍了神经网络的结够和sigmoid neuro，以及神经网络的目标函数和学习方法。但是没有讲如何调整权重，通常是需要对目标函数求导，也就是说回避了对目标函数求导这个问题。这一节就将讲述这个问题。

---

关于代价函数的两个假设

反向传播算法的目标是计算代价函数对$w,b$的偏微分$\frac{\partial C}{ \partial w}$和$\frac{\partial C}{ \partial b}$。这里拿二次代价函数为例子，二次代价函数形式如下：
$C = \frac{1}{2n} \sum_x{||y(x)-a^L(x)||^2}$
这里，n是总的训练数据的对数，x是输入数据，y(x)是对应的期望的输出，L表示神经网络的层数，$a^L(x)$是当输入为x时输出层的激活函数的输出。

假设1

代价函数可以表示为总代价在每一个训练数据对上的平均代价。这样做就可以对每一个训练数据都对代价函数进行求导，在训练的时候是对每一个训练数据，每一次训练就可以调整一次权值。当前还一个好处就可以让代价和训练数据的数量无关。

假设2

代价函数可以写成神经网络的输出的函数。

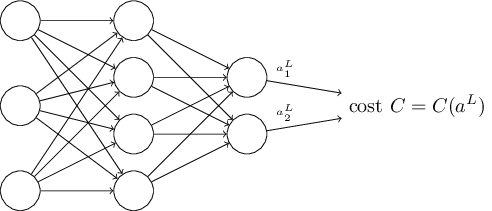
比如，对于上面说到的二次代价函数，对每一个输入$x$
$C = \frac{1}{2n} \sum_x{||y-a^L||^2}=\frac{1}{2}sum_j(y_j-a_j^L)^2$

---

反向传播的四个等式

反向传播主要涉及到计算代价函数的偏微分，对每一个系数的微分，$\frac{\partial C}{ \partial w_{jk}^l}$和$\frac{\partial C}{ \partial b_j^l}$。为了计算这些偏微分，首先引入一个变量$\delta_j^l$，该变量表示第$l$层的第$j$个神经元的误差。我们定义误差为：$\delta_j^l = \frac{\partial C}{\partial z_j^l}$。

首先是输出层的误差$\delta^L$：
$\delta_j^L=\frac{\partial C}{\partial a_j^L}\sigma'(z_j^L) --(BP1)$
这是根据误差的定义来的，前面一项表示$\frac{\partial C}{\partial a_j^L}$表示输出层第$j$个神经元的输出值的变化对代价函数的影响，如果代价函数不对某一个特别的神经元的输出敏感，则该项就会比较小。第二项$\sigma'(z_j^L)$衡量激活函数在$z_j^L$变化的快慢。
根据定义，$\delta_j^L=\frac{\partial C}{\partial z_j^L}=\frac{\partial C}{\partial a_j^L}\frac{\partial a_j^L}{\partial z_j^L} = \frac{\partial C}{\partial a_j^L}\sigma'(z_j^L)$.
把（BP1）写成向量的形式，$\delta^L=∇_aC⊙\sigma'(z^L)=(a^L-y)⊙\sigma'(z^L) --(BP1a)$

用$l+1$层的误差项来表示$l$层的误差项
$\delta^l=((w^{l+1})^T\delta^{l+1})⊙\sigma'(z^l) --(BP2)$
这里可以看到，第$l$的误差是把第$l+1$层的误差通过这两层之间的权重$w$联系起来，然后再与对应的神经元的激活函数的导数相乘，就得到了这两层神经元的误差之间的关系式，这个过程和神经网络的前向传播计算过程相似，所以该算法也被称为反向传播算法。
结合(BP1)(BP2)两个式子，就可以计算任意层的误差项。

证明：
$\delta_j^L=\frac{\partial C}{\partial z_j^l}$
$=\sum_k\frac{\partial C}{\partial z_k^{l+1}}\frac {\partial z_k^{l+1}}{\partial z_j^l}$
$=\sum_k\frac {\partial z_k^{l+1}}{\partial z_j^l} \delta_k^{l+1}$
又因为有$z_k^{l+1}=\sum_jw_{kj}^{l+1}\sigma'(z_j^l)$+b_k^{l+1}，所以$\frac {\partial z_k^{l+1}}{\partial z_j^l}=w_{kj}^{l+1}\sigma'(z_j^{l})$
$=\sum_kw_{kj}^{l+1}\sigma'(z_j^{l}) \delta_k^{l+1}$
$=((w^{l+1})^T\delta^{l+1})⊙\sigma'(z^L)$

代价对偏置项 $b_j^l$ 的导数
$\frac{\partial C}{\partial b_j^l}=\delta_j^l--(BP3)$
刚好就是我们前面定义的误差项。改写为向量形式。$\frac{\partial C}{\partial b}=\delta$

代价对权重 $w_{ij}$ 的导数
$\frac{\partial C}{\partial w_{jk}^l}=a_k^{l-1}\delta_j^l--(BP4)$
这样就可以把$w_{ij}$ 的导数用$a^{l-1}$和$\delta^l$表示了，而这两者已经都计算出来了。改写一下:
$\frac{\partial C}{\partial w}=a_{in}\delta_{out}$
这里可以理解为$a_{in}$是神经元的激活输入，$\delta_{out}$是神经元的激活输出，连接两者的权重是$w$，注意，这里的输入、输出是相对反向而言的。

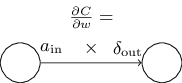
可以看出，当$a_{in}$很小时，导数$\frac{\partial C}{\partial w_{jk}}$也将会比较小，这情况下，就说学习速率很慢。

小结

---

反向传播算法

1. 输入 $x$，设置输入层对应的激活$a^1$
2. 前向传播，对$l=2,3,...,L$，计算$z^l=w^la^{l-1}+b^l,a^l=\sigma(z^l)$
3. 输出层误差，计算向量$\delta^L=∇_aC⊙\sigma'(z^L)$
4. 反向传播误差，对$l=L-1,L-2,...2$，计算$\delta^l=((w^{l+1})^T\delta^{l+1})⊙\sigma'(z^l)$

5. 输出，得到代价函数的梯度$\frac{\partial C}{\partial w_{jk}^l}=a_k^{l-1}\delta_j^l，\frac{\partial C}{\partial b_j^l}=\delta_j^l--(BP3)$

   在实际中，使用的是最小堆随机梯度下降法mini-batch SGD，每次选定m个训练样本，对每一样本求导数，然后再平均，再应用到梯度下降的表达式中。

---

反向传播的代码

class Network(object):
...
    def update_mini_batch(self, mini_batch, eta):
        """Update the network's weights and biases by applying
        gradient descent using backpropagation to a single mini batch.
        The "mini_batch" is a list of tuples "(x, y)", and "eta"
        is the learning rate."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            #累加导数项
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw 
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb 
                       for b, nb in zip(self.biases, nabla_b)]

大部分工是由 delta_nabla_b, delta_nabla_w = self.backprop(x, y) 这行代码做的。是用函数backpro计算两个导数项。

class Network(object):
...
   def backprop(self, x, y):
        """Return a tuple "(nabla_b, nabla_w)" representing the
        gradient for the cost function C_x.  "nabla_b" and
        "nabla_w" are layer-by-layer lists of numpy arrays, similar
        to "self.biases" and "self.weights"."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        #首先计算最后一层的偏导数
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        #公式(BP3)
        nabla_b[-1] = delta 
        #公式(BP4)
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        #在逐层反向传播，计算每一层的导数
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)
...

    def cost_derivative(self, output_activations, y):
        """Return the vector of partial derivatives \partial C_x /
        \partial a for the output activations."""
        return (output_activations-y) 

def sigmoid(z):
    """The sigmoid function."""
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    """Derivative of the sigmoid function."""
    return sigmoid(z)*(1-sigmoid(z))

---

彩蛋-为什么说反向传播是一种比较快的算法？

在其他地方很少有提到这一点的，大多数资料都会直接给你开始介绍反向传播算法的具体细节，然后说这是一个很有效的算法。实际上当神经元很多的时候，每两层的神经元之间两两连接，会有很多参数，计算起来还是会比较慢。那为什么说反向传播是一种比较快的算法呢？
要知道这一点，需要了解一些神经网络的历史。
最开始的时候，计算每一个权重的导数是通过近似的方法：

$$\begin{eqnarray} \frac{\partial C}{\partial w_{j}} \approx \frac{C(w+\epsilon e_j)-C(w)}{\epsilon} \end{eqnarray}$$
这个式子看上去很简单，也很好理解，比反向传播算法看上去简单多了。但是，实际上是很难计算的。因为需要对每一个$w_j$，都做一个比较小的扰动，然后计算扰动后的代价函数，然后才能计算代价函数对$w_j$的导数，如果有10000个参数，那就要计算10000次代价函数，而计算代价函数，必须要得到当前参数下神经网络的输出，结果就是要把神经网络的前向传播过程计算10000次！！
相反，对于反向传播算法，只需要对当前的输入 x <script id="MathJax-Element-20036" type="math/tex">x</script>计算一次，得到神经网络的预测值，然后通过反向传播算法，反向传播一次，就可以计算出所有的导数了！所以尽管反向传播看上去很复杂，但是确实是很有效！很快！
反向传播算法时在1980s提出来的，提出来之后，神经网络才开始又蓬勃发展了。

参考

neuralnetworksanddeeplearning.com/chap2.html