斐波那契数列(Fibonacci)及其拓展

其实斐波那契数列这种东西我小学就学过，但是只是当时并没有学得这么清晰透彻，现在让我们一起来领略一下有关斐波那契数列的一些算法吧（初学者可以看看）
斐波那契数列：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …[1]
如果设F(n）为该数列的第n项（n∈N*），那么这句话可以写成如下形式：[1]
显然这是一个线性递推数列。[1]
通项公式
（这是封闭公式，也就是说这个公式对于小的数来说并不十分的精确）
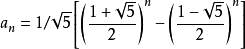
1.当n<=45时，直接就可以算
2.当n<=1000时直接高精度，如果你高精度不会的话可以看一下用java写大数加法，效果还是蛮不错的
3.当n>1000时，就可以用这个公式了，不过这个公式对付什么求斐波那契数列得前几位还可以，要是求后几位怎么办呢，放心，后面会有讲解的，要耐心往后慢慢读哦。
下面我们举个栗子
一.比如说我要求f（n）的前四位怎么办呢？
我们知道1234567可以写成1234.567*10^（len-4），有的人会问len怎么求呢，我们知道比如说99，它的len是2，那我们就可以用一下log10，之后发现小于2，这就对了，最大的两位数log10之后都小于2，那么我们取整一下再加个1，有没有发现什么规律呢，就是log10你求的数，取整之后再加一，就是len的值，之后让我们继续操作，因为我们要求的是前四位，那我们不妨把它设成d，设给出的数是x，
之后就会有这样一个等式x=d.567*10^（len-4），
之后让我们进行一步取对数运算，log10x=log10（d.567+len-4），
之后继续进行化简log10（x+4-len）=log10(d.567);
之后10^（log10（x+4-len）=d.567；
现在有人问了，x怎么求呢，当然是直接套公式了啊，不过一般当n超过45之后，
（（1-sqrt（5））/2）^n就已经太小了，故一般可以舍去，不影响。
y=log10(1/sqrt(5))+n*log10((1+sqrt(5))/2)+4-(int)(log10(1/sqrt(5))+n*log10((1+sqrt(5))/2)+1);
之后再int（pow（10，y））就OK了
二.如果要是计算后4位怎么办呢？
那就按照递推公式每求一次对10000取余就好了啊
注意，如果遇到负数那又应该怎么办呢，
举个栗子：-11%3=-2，此时我们应该令（-2+3）%3=1；
另外在此处说一下下面几个公式：
1.(a+b)%m=(a%m+b%m)%m;
2.(a*b)%m=(a%m*b%m)%m;
3.a^n%m=(a%m)^n;
下面让我们简单的看一下快速幂是怎么来的，看完这个之后，就知道那么简短的代码是怎么进行操作的了，下面让我们举个栗子
7^83%5=（7*7^82）%5；
=（2*（49^41））%5；
=(2*4^41)%5;
=(2*4*4^40)%5;
=(3*1^20)%5;
=3;
哈哈， 其实就是这样一个简单的过程，你懂了没？
注意了注意了，下面就要进入最重要的环节了——矩阵连乘，学过线性代数的小伙伴接下来的部分应该都能看懂的（只要你会最基本的矩阵乘法其实就可以了，不要担心）
而且，并不是只有斐波那契数列才可以用矩阵连乘，任何一个关于F（n）的表达式都可以用矩阵连乘哦，真实一个神器呢，下面让我们直接用一道例题来给大家举个栗子
hit2255
http://acm.hit.edu.cn/hoj/problem/view?id=2255
Maybe ACMers of HIT are always fond of fibonacci numbers, because it is so beautiful. Don’t you think so? At the same time, fishcanfly always likes to change and this time he thinks about the following series of numbers which you can guess is derived from the definition of fibonacci number.
The definition of fibonacci number is:
f(0) = 0, f(1) = 1, and for n>=2, f(n) = f(n - 1) + f(n - 2)
We define the new series of numbers as below:
f(0) = a, f(1) = b, and for n>=2, f(n) = p*f(n - 1) + q*f(n - 2),where p and q are integers.
Just like the last time, we are interested in the sum of this series from the s-th element to the e-th element, that is, to calculate
Great!Let’s go!
Input
The first line of the input file contains a single integer t (1 <= t <= 30), the number of test cases, followed by the input data for each test case.
（此处的图片请点开链接）http://acm.hit.edu.cn/hoj/static/img/pic/100309.bmp
Each test case contains 6 integers a,b,p,q,s,e as concerned above. We know that -1000 <= a,b <= 1000,-10 <= p,q <= 10 and 0 <= s <= e <= 2147483647.
Output
One line for each test case, containing a single interger denoting S MOD (10^7) in the range [0,10^7) and the leading zeros should not be printed.
Sample Input
2
0 1 1 -1 0 3
0 1 1 1 2 3
Sample Output
2
3

#include <iostream>
#define Mod 10000000
const int MAX=3;
using namespace std;
typedef struct
{
    long long m[MAX][MAX];
} Matrix;
Matrix P= {0,0,0,
           1,0,0,
           0,0,1,
          };
Matrix I= {1,0,0,
           0,1,0,
           0,0,1,
          };
Matrix mm(Matrix a,Matrix b)
{
    Matrix c;
    for(int i=0; i<MAX; i++)
        for(int j=0; j<MAX; j++)
        {
            c.m[i][j]=0;
            for(int k=0; k<MAX; k++)
            {
                a.m[i][k]=(a.m[i][k]%Mod+Mod)%Mod;
                b.m[k][j]=(b.m[k][j]%Mod+Mod)%Mod;
                c.m[i][j]+=(a.m[i][k]*b.m[k][j])%Mod;
            }
            c.m[i][j]=(c.m[i][j]%Mod+Mod)%Mod;
        }
    return c;

}
Matrix quickpow(long long n)
{
    Matrix x = P, y = I;
    while(n>=1)
    {
        if(n&1)
        y=mm(y,x);
        n=n>>1;
     x=mm(x,x);
     }
    return y;

}
int main()
{
    int a,b,p,q,s,e,t;
    Matrix tmp,tmp1;
    cin>>t;
    long long sum,sum1,sum2;
    while(t--)
    {
        sum=0;
        sum2=0;
        cin>>a>>b>>p>>q>>s>>e;
        P.m[0][0]=p;
        P.m[0][1]=q;
        P.m[2][0]=p;
        P.m[2][1]=q;
        if(e>=2)
        {
            tmp=quickpow(e-1);
            sum=(tmp.m[2][0]*b)%Mod+(tmp.m[2][1]*a)%Mod+(tmp.m[2][2]*(a+b))%Mod;

            sum=(sum+Mod)%Mod;
        }
        if(e==1)
        {
            sum=((a+b)%Mod+Mod)%Mod;
        }
        if(e==0)
            sum=(a%Mod+Mod)%Mod;
        if(s==0)
            sum1=0;
        if(s==1)
            sum1=(a%Mod+Mod)%Mod;
        if(s==2)
            sum1=((a+b)%Mod+Mod)%Mod;
        if(s>=3)
        {
            tmp1=quickpow(s-2);
            sum1=(tmp1.m[2][0]*b)%Mod+(tmp1.m[2][1]*a)%Mod+(tmp1.m[2][2]*(a+b))%Mod;
            sum1=(sum1+Mod)%Mod;
        }
        sum2=(sum-sum1+Mod)%Mod;
        cout<<sum2<<endl;
    }

    return 0;
}

其实这个题我们也可以不分类讨论的,把中间矩阵的最后一项改成s（n-2），之后左面的矩阵和右面的矩阵都变一下，使得左面的矩阵的n次幂对应的是右面矩阵正好能求出s（n），至于画图什么的怎么推的就自己去试试吧
补充一个公式

下面最后再说一点关于大数加法的问题，之前我的博客里也有，但是我想在这里汇总一下举个栗子hdu1250
高精度法

#include <iostream>
#include <stdio.h>
using namespace std;
int a[8000][255]= {{0}};
int n,k,ans,i,j,m;
int main()
{
    for( i=1; i<5; i++)a[i][1]=1;
    for( i=5; i<8000; i++)
        for(j=1; j<255; j++)
        {
            a[i][j]+=a[i-1][j]+a[i-2][j]+a[i-3][j]+a[i-4][j];
            a[i][j+1]+=a[i][j]/100000000;
            a[i][j]=a[i][j]%100000000;
    }
    while(scanf("%d",&n)!=EOF)
    {
        for(j=254; j>0; j--)
            if(a[n][j]!=0)
            {
                k=j;
                cout<<a[n][j];
                break;

            }
        for( m=k-1; m>0; m--)
            printf("%.8d",a[n][m]);
            cout<<endl;


    }
    return 0;
}

java大数法

import java.io.*;
import java.math.BigInteger;
import java.util.*;
public class Main {
    public static void main(String[] args)
    {
        Scanner cin=new Scanner(System.in);
        BigInteger a[]=new BigInteger[10500];
        a[1]=BigInteger.valueOf(1);
        a[2]=BigInteger.valueOf(1);
        a[3]=BigInteger.valueOf(1);
        a[4]=BigInteger.valueOf(1);
        for(int i=5;i<10500;i++)
            a[i]=a[i-1].add(a[i-2]).add(a[i-3]).add(a[i-4]);
        int n;
        while(cin.hasNext())
        {
            n=cin.nextInt();
            System.out.println(a[n]);
        }
    }

}

这篇博客已经接近尾声，不过说实话，有点累但是也很快乐，期待下一次的博客之旅。