(ps:主要依照课本目录总结一下要记的公式期望和方差,概念去课本上看)
2.1、随机变量及其分布
一、随机变量的概念
随机变量一般用大写XYZ表示,取值一般用小写xyz表示
二、离散型随机变量的概率分布
三、分布函数
分布函数性质
1、单调性:若x1<=x2,则F(x1)<=F(x2);(单调递增)
2、F(负无穷)=0,F(正无穷)=1
2、右连续性:F(x+0)=F(x)
四、离散型随机变量的分布函数
区间概率表示:(概率分布p与分布函数F之间转换)
p(x<=a)=F(a)
p(x<a)=F(a-0)
p(x=a)=F(a)-F(a-0)
p(a<x<=b)=F(b)-F(a)
p(a<=x<=b)=F(b)-F(a-0)
p(a<x<b)=F(b-0)-F(a)
p(a<=x<b)=F(b-0)-F(a-0)
p(a<x)=p(x>b)=1-F(a)
由于连续型p(x=a)=0,所以若F(x)连续,则4-7相等
五、连续型随机变量及其概率密度
概率密度性质
1、f(x)>=0,在其定义域内
2、全定义域积分为1
2.2、随机变量的数字特征
一、离散型随机变量的数学期望
取值与概率乘积求和
二、连续型随机变量的数学期望
取值与概率乘积求积分
三、随机变量函数的数学期望
四、数学期望的性质
1、对任意常数a,E(a)=a
2、如果E(X),E(Y)存在,对任意实数a
E(X+Y)=E(X)+E(Y),E(XY)=E(X)E(Y),E(X+a)=E(X)+a
五、随机变量的方差
D(X)=E([X−E(X)]^2)
D(X)=E(X^2)−E2(X)
六、方差的性质
Da=0
D(X+a)=D(X)
D(aX)=a^2D(X)
2.3、常用的离散型分布
一、退化分布
不分布,以概率1取某一常数a
期望和方差
E(X)=a
D(X)=0
二、两点分布
1、定义
在一次伯努利试验中,,若用X记事件A出现的次数,
,
称X服从两点分布或(0-1)分布。
2、期望和方差
E(X)=p
D(X)=p(1-p)
三、均匀分布
1、定义
共有n次不可能的取值,且取每一个值的可能性都相等,即
2、期望和方差
四、二项分布
1、定义
在n重伯努利试验中,若事件A出现的次数记为X,随机变量X可能的值是0,1,2,...,n,相应概率分布为
式中,且
,则称X服从参数为n,p的二项分布,记作
.
2、期望和方差
E(X)=np
D(X)=npq
五、几何分布
1、定义
在伯努利试验中,考虑事件A首次出现时的试验次数X的分布。X的所有可能取值是集合,事件
表示A首次出现是在第k次试验,即前k-1次试验都出现
,而第k次试验出现A,这一事件的概率为
上式是几何级数的一般项,因此称为几何分布。记作。显然有
2、期望和方差
E(X)=1/p
D(X)=q/p^2
六、超几何分布
1、定义
现有N件产品,其中有M件次品,今从中任取n件(不放回抽取),则这n件中所含的次品数X是一离散型随机变量,其概率分布为
其中。通常称这个概率分布为超几何分布。记作
。
七、泊松分布
1、定义
如果随机变量X的概率分布为
式中是常数,则称X服从以
为参数的泊松分布,记作
。
自然界中的很多稀疏现象都服从或近似服从泊松分布,所以泊松分布又称为稀疏现象律。
泊松分布的最可能值为,若
为整数,则最可能值为
或
.
2、期望和方差
E(X)=D(X)=
2.4、常用的连续型分布
一、均匀分布
1、定义
在取值范围(a,b)内取得任意一点的概率相等,记为X~U(a,b)
2、期望和方差
E(X)=(a+b)/2
D(X)=(b-a)^2/12
二、指数分布
1、定义
若随机变量X的概率密度为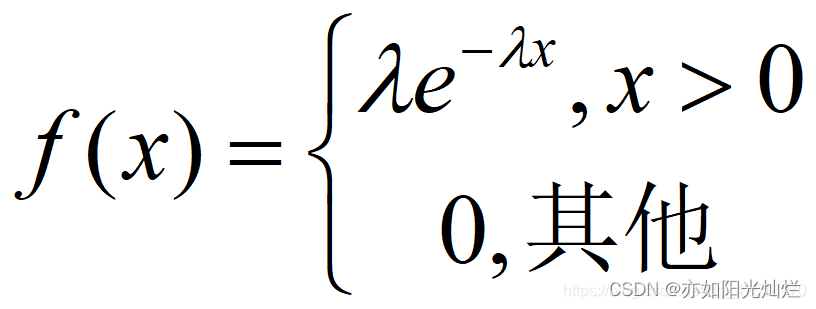
则称X服从参数为λ的指数分布,记为X~e(λ)
因此得到分布函数为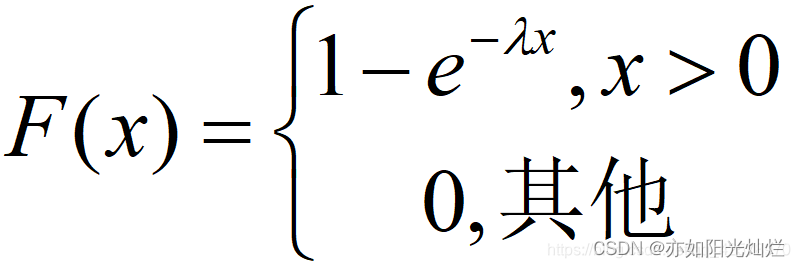
2、期望和方差
E(X)=1/λ
D(X)=1/λ^2
三、正态分布
1、定义
概率密度函数为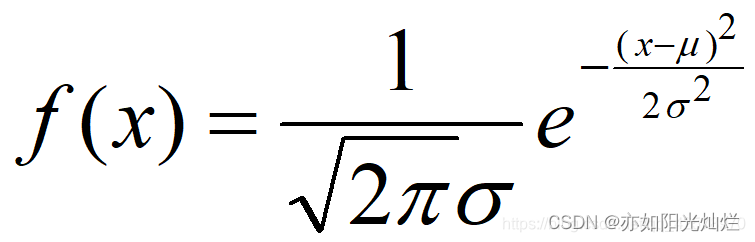
则称X服从参数为μ,σ的正态分布,记为X~N(μ,σ^2)
分布函数为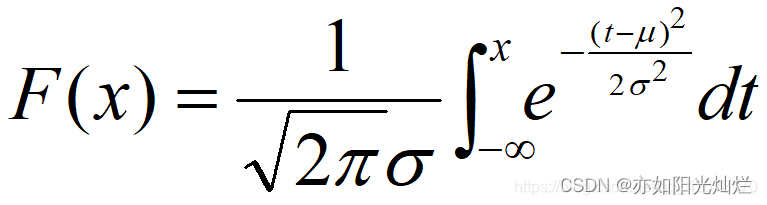
![]()
2、期望和方差
E(X)=
D(X)=
3、标准正态分布
特别的,当μ=0,σ=1时,X服从标准正态分布,此时概率密度函数写为φ(x),分布函数写为Φ(x)
因为,若X~N(μ,σ^2),则Z=(X-μ)/σ服从标准正态分布,所以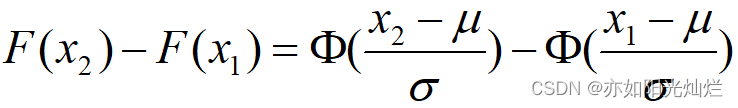







 本文概述了随机变量的基本概念,包括离散型和连续型随机变量的分布函数、概率密度、数学期望、方差及其性质。详细介绍了常见分布如两点分布、均匀分布、二项分布、几何分布、超几何分布、泊松分布、均匀分布、指数分布和正态分布的期望和方差计算。
本文概述了随机变量的基本概念,包括离散型和连续型随机变量的分布函数、概率密度、数学期望、方差及其性质。详细介绍了常见分布如两点分布、均匀分布、二项分布、几何分布、超几何分布、泊松分布、均匀分布、指数分布和正态分布的期望和方差计算。














 215
215

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








