【算法设计与分析】动态规划问题Python

例1：小明周末要参加学校组织的跳蚤市场活动，他准备了足球、旱冰鞋、随身听和单词书四件物品进行交易，要用他的书包把这些物品带到学校。各物品的重量w和价值v如下图所示，小明书包的最大承重量为9（忽略单位），请你帮助他找到最合理的搭配方案，使他能用书包带到学校的物品价值最大

1算法思路

这道题的算法思路是使用动态规划来解决。将问题分解为不同的子问题，并找到最优的子结构来得到最终的解。算法的步骤具体如下：

定义状态：令dp[i][j]表示前i件物品放入容量为j的书包中所能获得的最大价值。

初始化状态：将dp数组初始化为0，表示没有物品或容量为0时的价值为0。

状态转移方程：对于每个物品i和每个容量j，我们可以选择放入或不放入该物品。如果放入物品i，则dp[i][j] = dp[i-1][j-w[i]] + v[i]；如果不放入物品i，则dp[i][j] = dp[i-1][j]。我们选择这两种情况中的最大值作为dp[i][j]的值。

边界条件：当i=0时，dp[0][j] = 0，表示没有物品时价值为0。

遍历物品和容量：使用双重循环遍历每个物品和每个容量，根据状态转移方程计算dp数组的值。

结果输出：最后，dp[n][W]中的值即为最大价值，其中n为物品的数量，W为书包的最大承重量。

2手算过程

通过以上算法，计算的过程如下：

	1	2	3	4	5	6	7	8	9
足球w=2 v=5	0	足球5	足球5	足球5	足球5	足球5	足球5	足球5	足球5
旱冰鞋w=4 v=4	0	足球5	足球5	足球5	足球5	足球+旱冰鞋9	足球+旱冰鞋9	足球+旱冰鞋9	足球+旱冰鞋9
随身听w=5 v=6	0	足球5	足球5	足球5	随身听6	足球+旱冰鞋9	足球+随身听11	足球+随身听11	足球+随身听11
单词书w=3 v=2	0	足球5	足球5	足球5	足球+单词书7	足球+旱冰鞋9	足球+随身听11	足球+随身听11	足球+随身听11

3代码实现

该程序基于 Python3.11语言编写

"""背包问题""" def full_pack(max_weight, weights, values, n):     dp = [[0 for i in range(max_weight + 1)] for j in range(n+1)]     for i in range(1, n+1): #外循环：4个货物        for j in range(1, max_weight+1): #内循环：1-9重量           if weights[i-1] <= j: #如果可以装下当前货物               #当前货物价值+前一行剩余容量可容纳的最大价值 和 正上方数据比较，取最大的              dp[i][j] = max(values[i-1] + dp[i-1][j-weights[i-1]], dp[i-1][j])           else: #如果装不下，复制表格正上方              dp[i][j] = dp[i-1][j]     # 输出选取方案     selected_items = []     j = max_weight     for i in range(n, 0, -1):        if dp[i][j] != dp[i-1][j]:           selected_items.append(i-1)           j -= weights[i-1]     return dp[n][max_weight], selected_items weights = [2, 4, 5, 3] values = [5, 4, 6, 2] items_name = ["足球", "旱冰鞋", "随身听", "单词书"] max_weight = 9 num_items = len(weights) max_value = full_pack(max_weight, weights, values, num_items) print("最大价值为：", max_value[0]) print("最佳的选取方案为：") for i in max_value[1]:     print(items_name[i])

4代码解释

代码使用动态规划算法，目标是在给定一组物品的重量和价值的情况下，确定在不超过背包最大重量限制的情况下，能够获得的最大价值。

代码中的full_pack函数接受四个参数：max_weight表示背包的最大重量限制，weights表示每个物品的重量列表，values表示每个物品的价值列表，n表示物品的数量。

函数内部使用一个二维数组dp来存储子问题的解。dp[i][j]表示在前i个物品中选择一些物品放入容量为j的背包时能够获得的最大价值。

代码通过两层循环遍历所有可能的物品组合和背包容量。对于每个物品，如果其重量小于等于当前背包容量，则可以选择将其放入背包或不放入背包。根据动态规划的思想，我们比较将该物品放入背包后的总价值与不放入背包的总价值，取其中较大的值作为当前状态的最优解。

最后，函数返回dp[n][max_weight]，即在所有物品中选择一些物品放入容量为max_weight的背包时能够获得的最大价值。

在代码的最后部分，定义物品的重量和价值列表，以及背包的最大重量限制。然后调用full_pack函数计算最大价值，并将结果打印输出。

我还编写了一段输出选取方案的代码，便于输出最佳的组合序列。首先，创建一个空列表selected_items用于存储选取的物品索引。然后，从最大重量max_weight开始遍历，通过比较动态规划表dp中当前物品和上一个物品在相同重量下的价值，判断是否选择了当前物品。如果选择了当前物品，则将其索引添加到selected_items列表中，并更新剩余重量j。最后，返回最大价值和选取的物品索引列表。

5结果验证

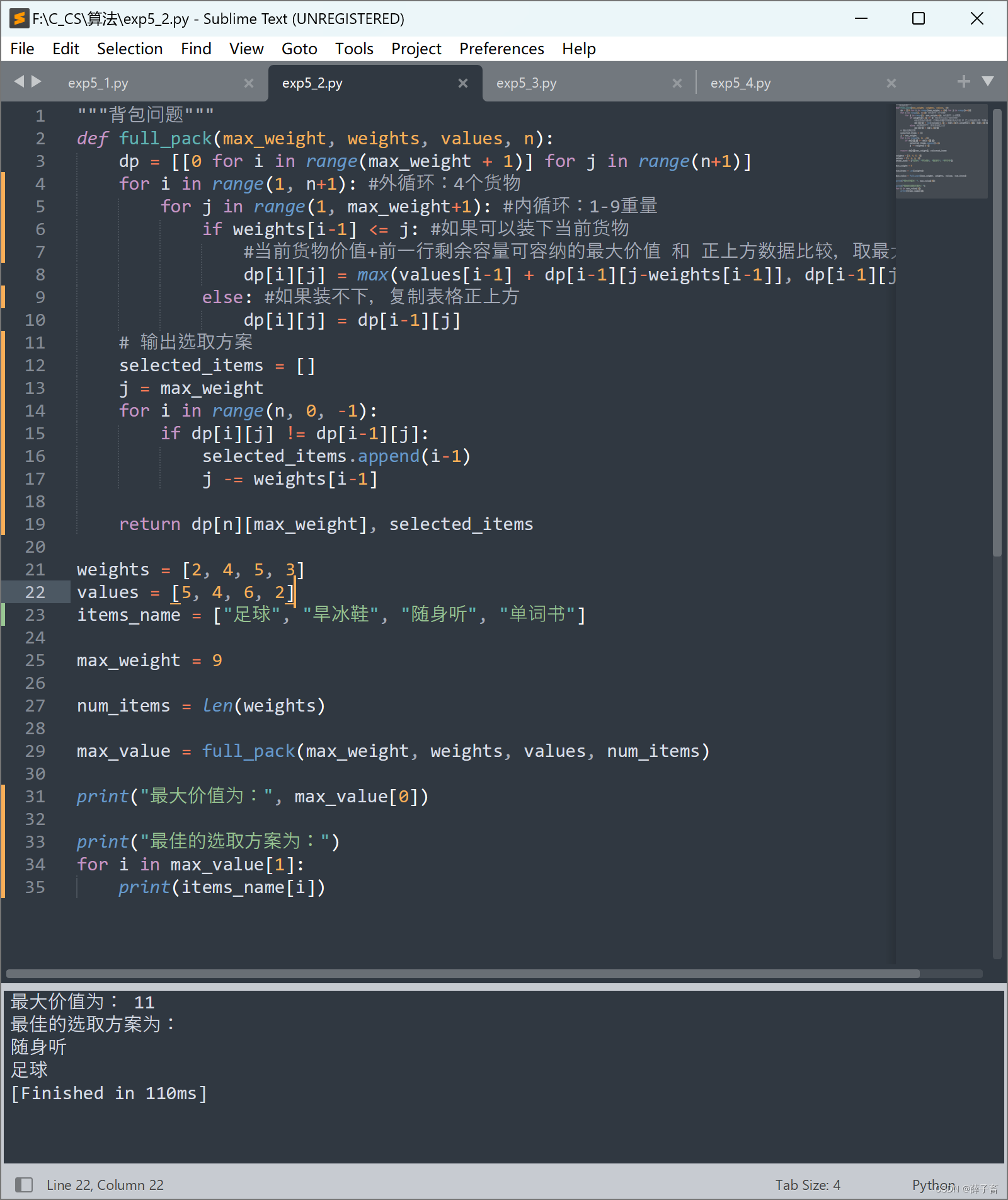
输出结果如图

最大价值为： 11

最佳的选取方案为：随身听+足球

与手算结果一致。

例2：某地有6座矿场，每座矿场的黄金储量和需要挖掘的工人数量如下所示。假设参与挖矿的工人总数是16人，且每座矿场要么全挖，要么不挖，不能派出一半人挖取一半金矿。要想得到尽可能多的黄金，应该选择挖取哪几座矿场呢？

1程序思路

这一题和题目二的思路是一样的，都是动态规划的背包问题。即在有限的工人数量下，如何选择矿场以获得最大的黄金产出。这是一个典型的背包问题，可以使用动态规划算法来解决。算法的步骤具体如下：

首先定义了一个名为full_pack的函数，该函数接收四个参数：max_weight（最大工人数量），weights（每个矿场所需的工人数量），values（每个矿场所需的黄金储量）和n（矿场数量）。函数的主要目的是计算在给定的最大重量限制下，如何选择矿场以获得最大的黄金产出。

在函数内部，首先创建了一个二维数组dp，用于存储子问题的解。然后使用两层循环遍历所有可能的货物组合和重量限制。对于每个货物，如果它可以被装入背包，那么就比较将其放入背包后的总价值与不放入背包的总价值，取其中较大的值作为当前状态的最优解。如果无法装入背包，则直接复制表格正上方的值。

接下来，输出选取方案。通过遍历dp数组的最后一行，找到最大价值所在的位置，然后根据这个位置回溯找到选择的矿场。最后将结果返回给调用者。

在主程序中，定义了两个列表：workers_in_need（每个矿场所需的工人数量）和gold_reserves（每个矿场所需的黄金储量）。然后调用full_pack函数，传入最大工人数量、工人需求列表、黄金储量列表和矿场数量，得到最大的黄金产出和选取方案。最后，打印出最大的黄金产出和最佳的选取方案。

2手算过程

根据算法的手算过程如下：

其中，表格第一列（1号6；500）意义：6代表需要6个工人，500表示黄金储量有500。

	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1号6；500	0	0	0	1 500	1 500	1 500	1 500	1 500	1 500	1 500	1 500	1 500	1 500	1 500
2号5；300	0	0	2 300	1 500	1 500	1 500	1 500	1 500	1+2 800	1+2 800	1+2 800	1+2 800	1+2 800	1+2 800
3号6；150	0	0	2 300	1 500	1 500	1 500	1 500	1 500	1+2 800	1+2 800	1+2 800	1+2 800	1+2 800	1+2 800
4号4；300	0	4 300	4 300	1 500	1 500	1 500	2+4 600	1+4 800	1+4 800	1+4 800	1+4 800	1+4 800	1+2+4 1100	1+2+4 1100
5号3；350	5 350	5 350	5 350	1 500	1 500	1 500	1+5 850	1+5 850	1+5 850	2+4+5 950	1+4+5 1150	1+4+5 1150	1+4+5 1150	1+4+5 1150
6号3；350	5 350	5 350	5 350	1 500	1 500	1 500	1+5 850	1+5 850	1+5 850	1+5+6 1200	1+5+6 1200	1+5+6 1200	2+4+5+6 1200	1+4+5+6 1500

3代码实现

该程序基于 Python3.11语言编写

"""实验3：背包问题的应用——挖矿问题""" def full_pack(max_weight, weights, values, n):     dp = [[0 for i in range(max_weight + 1)] for j in range(n+1)]     for i in range(1, n+1): #外循环：4个货物        for j in range(1, max_weight+1): #内循环：1-9重量           if weights[i-1] <= j: #如果可以装下当前货物               #当前货物价值+前一行剩余容量可容纳的最大价值 和 正上方数据比较，取最大的              dp[i][j] = max(values[i-1] + dp[i-1][j-weights[i-1]], dp[i-1][j])           else: #如果装不下，复制表格正上方              dp[i][j] = dp[i-1][j]     # 输出选取方案     selected_items = []     j = max_weight     for i in range(n, 0, -1):        if dp[i][j] != dp[i-1][j]:           selected_items.append(i-1)           j -= weights[i-1]     return dp[n][max_weight], selected_items workers_in_need = [6, 5, 6, 4, 3, 3] #每个矿场所需的工人 gold_reserves = [500, 300, 150, 300, 350, 350] #每个矿场所需的黄金储量 max_workers = 16 num_mine = len(workers_in_need) max_gold = full_pack(max_workers, workers_in_need, gold_reserves, num_mine) print("最大的黄金产出为：", max_gold[0]) print("最佳的选取方案为：") for i in max_gold[1]:     print(i+1)

4代码解释

函数full_pack(max_weight, weights, values, n)用于求解背包问题，其中max_weight表示背包的最大容量，weights表示每个物品的重量列表，values表示每个物品的价值列表，n表示物品的数量。

在函数内部，首先创建了一个二维数组dp，用于存储动态规划的状态。dp[i][j]表示在前i个物品中选择一些物品放入容量为j的背包中所能获得的最大价值。

使用两个嵌套的循环来填充dp数组。外层循环遍历所有物品，内层循环遍历从1到最大容量的所有可能的背包容量。

如果当前物品可以放入背包（即weights[i-1] <= j），则比较将该物品放入背包和不放入背包两种情况下的最大价值，取较大值作为dp[i][j]的值。

如果当前物品无法放入背包，则直接将上一行对应列的值复制给当前位置，即dp[i][j] = dp[i-1][j]。

最后，通过回溯dp数组，找到选取的物品方案。从最后一个物品开始，如果dp[i][j] != dp[i-1][j]，则说明第i个物品被选中，将其添加到选取方案中，并更新背包容量j。

返回最大黄金产出和选取方案。

在主程序中，定义了每个矿场所需的工人数和黄金储量，以及最大工人数和矿场数量。

调用full_pack函数求解最大黄金产出和最佳选取方案。

5结果验证

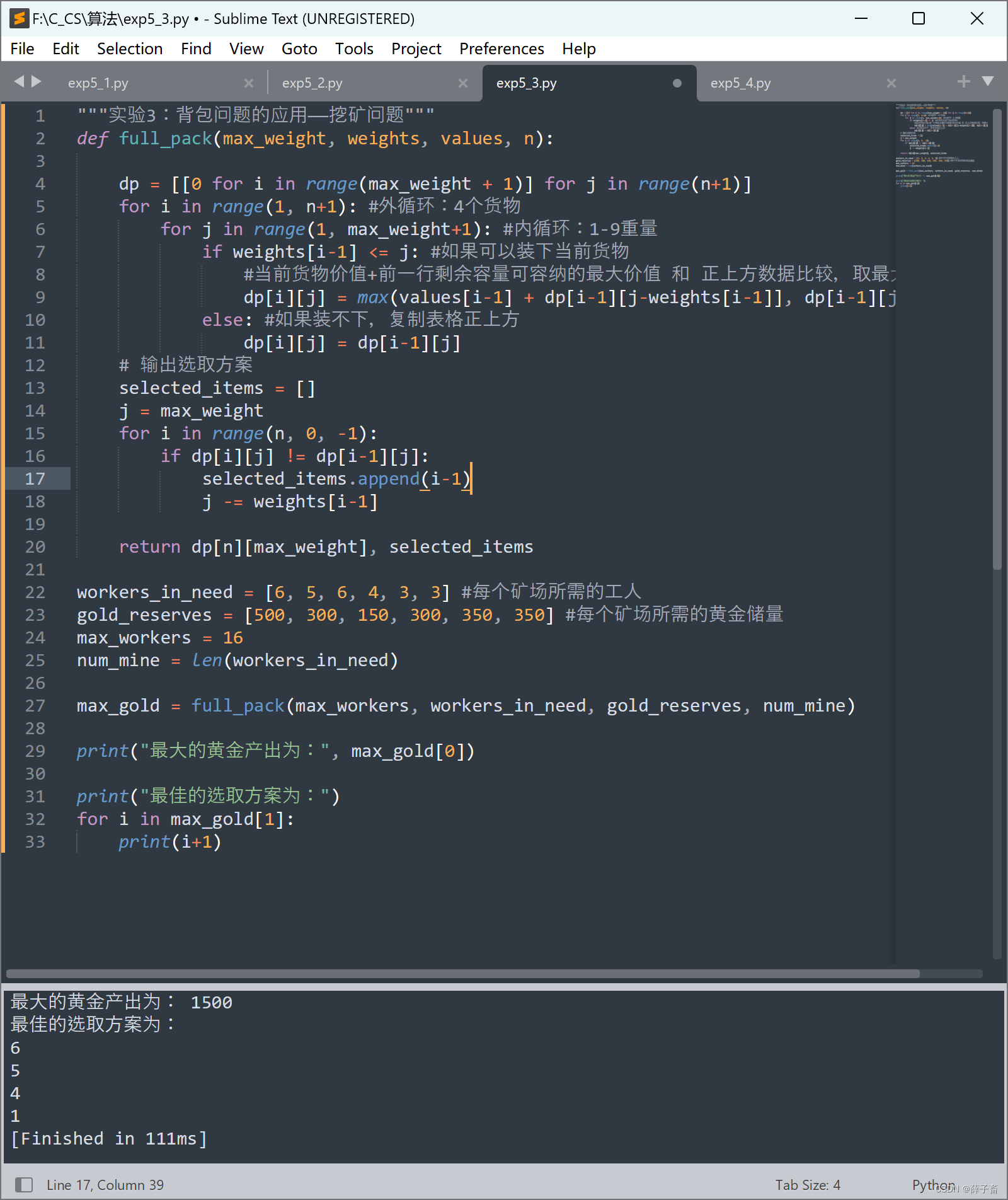
输出结果如图

最大的黄金产出为： 1500

最佳的选取方案为：6、5、4、1号矿场

与手算结果一致。