目录
6.3.1二叉树的其他操作
1.计算二叉树的结点数
二叉树的结点数总数等于其左右子树结点数加上1(根结点)。
2.计算二叉树的高度
任一的高度等于其左右子树高度的最大值加1,根结点的高度即为二叉树的高度。
3.二叉树的层次遍历
逐层访问树中的结点
举例
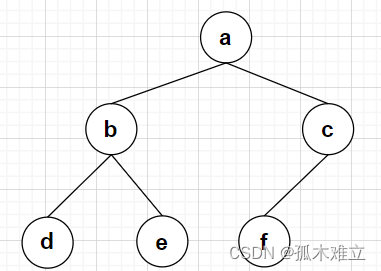
上图按层次遍历结果为abcdef.
4.由两个遍历序列构造二叉树
1)先序遍历和中序遍历
1.由先序遍历和中序遍历可以唯一确定一棵二叉树。
2.其思想就是通过不断的寻找根结点将给出的序列分为左右子树,依次如此直到所有和结点都被加入二叉树中。
3.举例图示:先序遍历为ABHFDECKG,中序遍历:HBDFAEKCG。
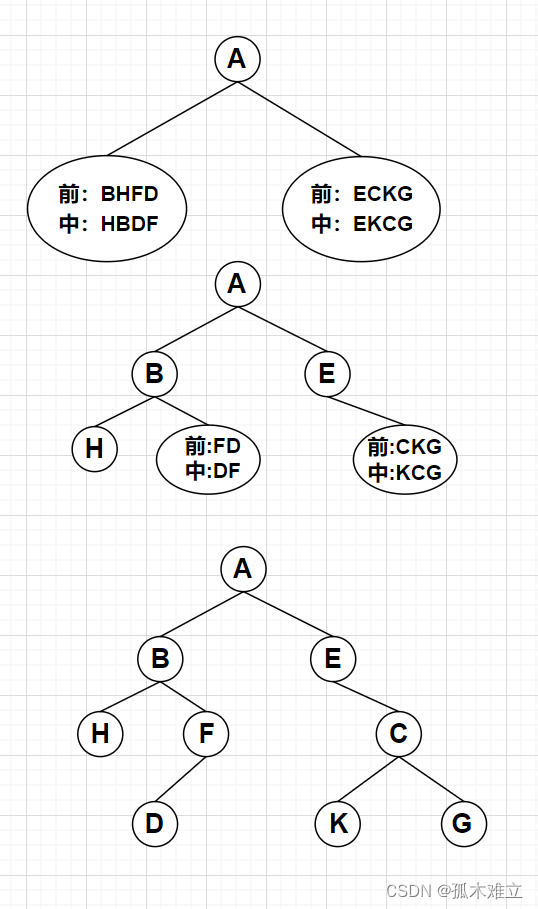
2)中序遍历和后序遍历
1.由中序遍历和后序遍历可以唯一的确定一棵二叉树。
2.其思想和先序遍历与中序遍历的组合一样都是通过不断的寻找根结点将给出的序列分为左右子树,依次如此直到所有和结点都被加入二叉树中。
3)先序遍历和后序遍历
此遍历不能唯一的识别一棵二叉树,是先序遍历和后序遍历在两种遍历序列组合中起到的作用是参考,但二者无法区分左右子树,因此无法唯一确认一棵二叉树。
5.关键值查找
通过指针去寻找二叉树中与指针变量值相等的结点,若不存在则返回NULL。
6.查找结点的父结点
使用遍历的方法检查每个结点的左右孩子是否符合查找条件
6.3.2线索二叉树
1.线索二叉树
线索二叉树即利用遍历二叉树所使用的二叉链表中的那些空的指针域用来标记某结点的前驱和后继的信息,指向前驱和后继的指针称为线索,加入了线索的二叉树即为线索二叉树。它是为了便于寻找前驱结点和后继结点。其次利用了那些原本二叉链表中的空指针域,使得空间浪费减少,以及算法的效率提高。降低了时间复杂度。
2.特征
1)结点中非空指针域保持不变
2)结点中空的左孩子指针域lchild指向该结点的前驱
3)结点中空的右孩子指针域rchild指向该结点的后继
4)新增的指针域:左标记区域为ltype和右标记区域rtype
a.
ltype为0时lchild指向该结点的左孩子,为1时指向该结点的前驱。
b.
rtype为0时rchild指向该结点的右孩子,为1时指向该结点的后继。
图示
![]()
3.操作
(1)构建线索二叉树的方法:
1)先根据给出的的序列画出二叉树的流图。
2)再根据流图写出该二叉树的先序,中序,后序遍历。
3)最后根据得到的先序遍历,中序遍历和后序遍历遍历序列各自对应找出某结点的前驱和后继结点使用虚线绘制线索二叉树。
(2)以某二叉树为例
1)给出流图
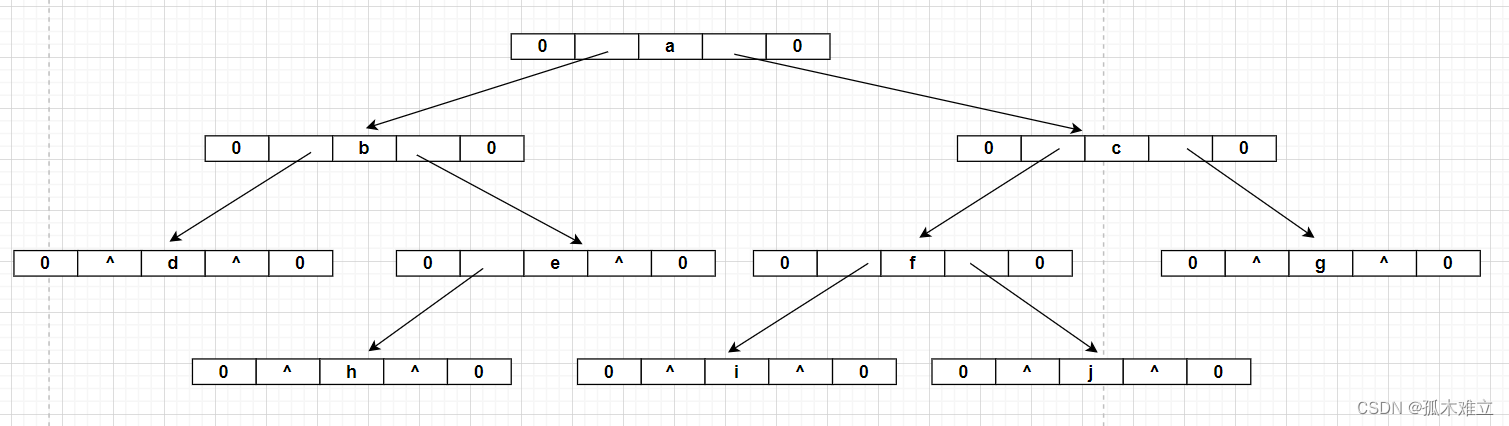
2)写出先序i遍历的结果:abdehcfgij.
3)根据先序遍历的结果绘制线索二叉树
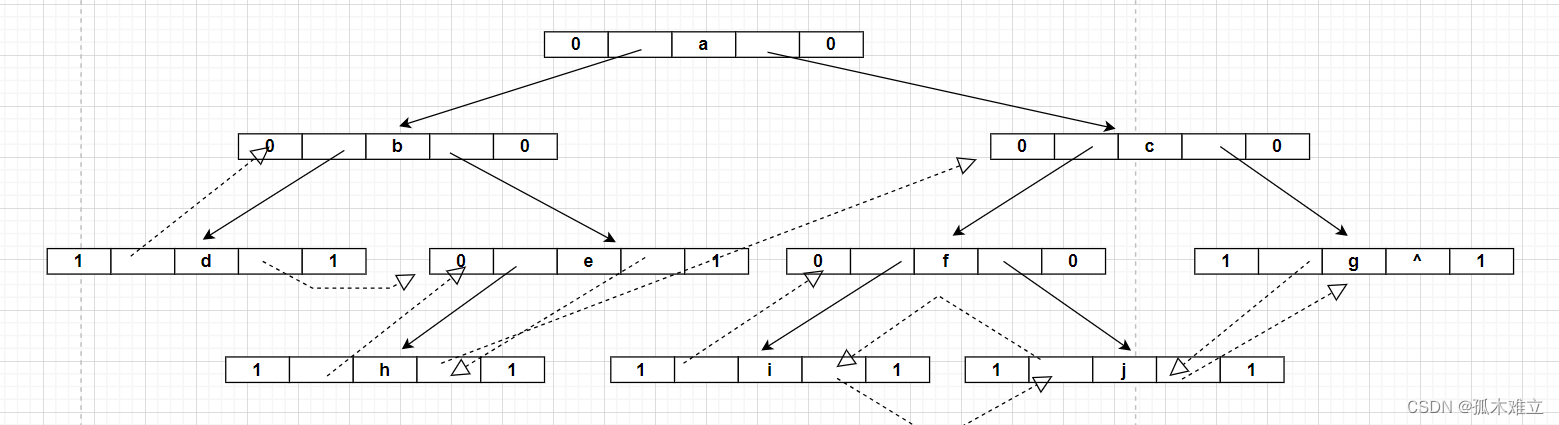
(4).中序线索二叉树求前驱和后继

前驱:BiThrTree GetNext(BiThrTree T) {
if (T->ltype == Thread) {
return T->lchild;
}
T = T->lchild;
while (T->rtype == Child)
T = T->rchild;
return T;
}
后继:BiThrTree GetNext(BiThrTree T) {
if (T->rtype == Thread) {
return T->rchild;
}
T = T->rchild;
while (T->ltype == Child)
T = T->lchild;
return T;
}
(5)线索化二叉树的算法
void inThreaded(BiThrTree& T) {
if (T == NULL) {
return;
}
inThreaded(T->lchild);
if (T->lchild == NULL) {
T->ltype = Thread;
T->lchild = prenode;
}
if (T->rchild == NULL) {
T->rtype = Thread;}
if (prenode != NULL) {
if (prenode->type = T) {
prenode->child = T;
}
}
prenode = T;
inThreaded(T->rchild);
}
(6)遍历算法
void Travse(BiThrTree T) {
while (T->ltype == Child) {
T = T->lchild;
}
while (T) {
cout << T->data << "";
T = GetNext(T);
}
}
6.3.3 Huffman树和Huffman编码
1.Huffman树
(1)定义
Huffman树即最优树,是一类带权路径长度(两结点间路径上的分支数)最短的二叉树,由其产生的编码称为Huffman编码。
(2)语术
1)路径:即一个结点到另一个结点之间的分支。
2)路径长度:两结点间历经上的分支数。
3)二叉树的带权路径长度:树中叶子结点的带权路径长度之和。
4)结点的带权路径长度:根结点到该结点之间的路径长度与该结点的权的乘积。
(3)举例
a.
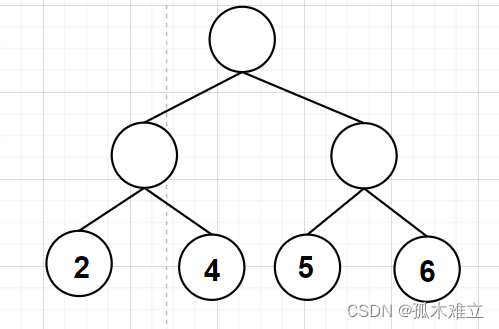
该图的WPL=35
b.
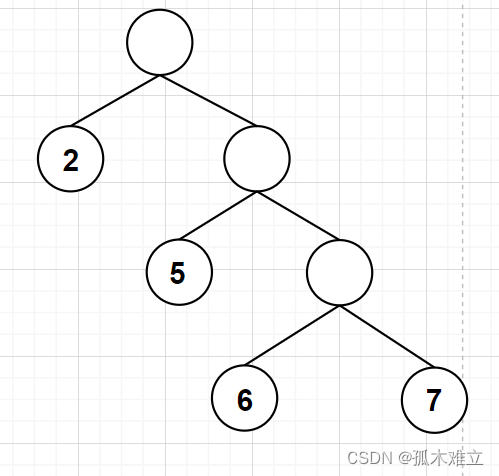
该图的WPL= 45
综上所述:Huffman树是所有可能的二叉树形态中,树的带权路径长度最小的二叉树(叶子节点固定) ,即选择图a。
(4)Huffman树的构造
1.规则:1)权值越大的叶子结点越靠近根结点,权值越小的叶子结点距离根结点越远。
2)只有度为0和度为2的结点,不存在度为1的结点。
2.步骤
1)初始为森林(构造森林全是根)
![]()
2)选取与合并(选用两小造新树)
![]()
3)删除与加入(删除两小添新人)
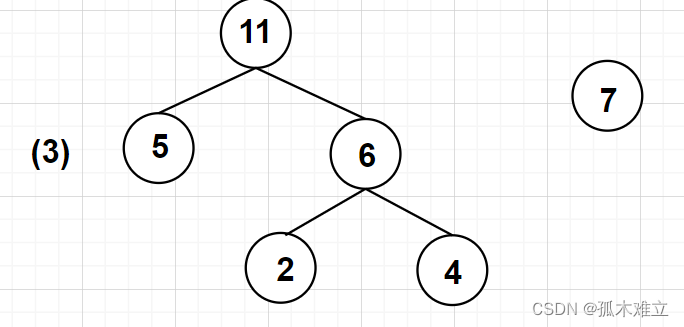
4)重复2)和3)(重复2),3)剩单根)
(5)Huffman树的存储结构
若结点数为n则分支结点数一定为n-1,Huffman树有2n-1个结点。
图示
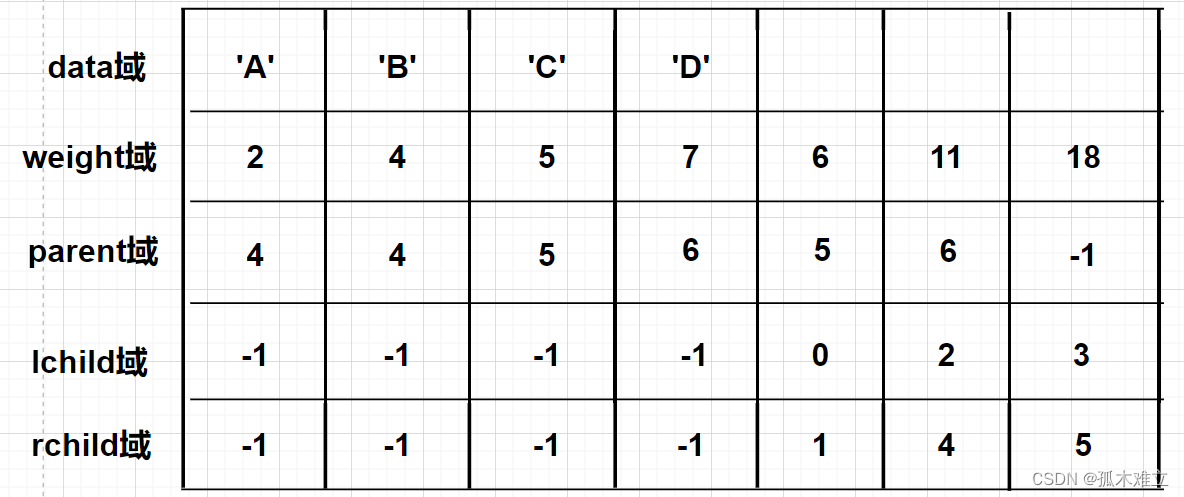
注:后三列存储的是新构造出来的根结点的权
(6)huffman树的构造算法
2.Huffman编码
(1)含义
根据各字符在字符串中出现的频率构造相应的Huffman,规定在Huffman树中左分支记作编码0,右分支记作编码1,根结点到每一个叶子结点的路径构成的0/1串就是该叶子结点的对应字符的Huffman编码。
Huffman树图示:
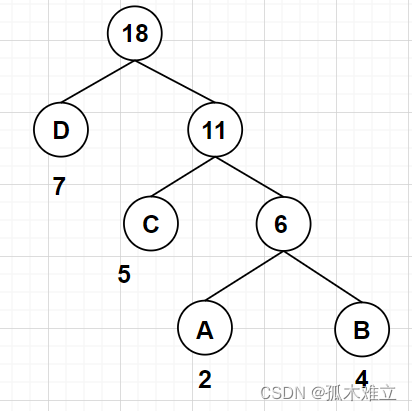
字符编码图示:
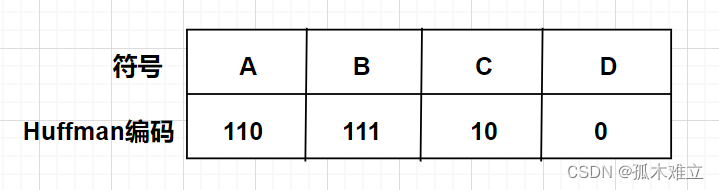
(2)Huffman编码算法
即求个叶子结点的编码
注:编码过程是从叶子结点回退至根结点,因此求编码时的顺序时Huffman编码的逆序。
(3)Huffman译码算法
即编码还原为字符
注:从根结点到叶子结点,source原Huffman树编码,,decode存放译码串。
6.3.4 总结
1.二叉链表
2.线索二叉树
3.最优二叉树(Huffman树)
代码能力有限,有些算法自己写了运行不出来也就没有展示,有幸看到的各位可以去别处补充一下代码知识。





















 505
505











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








