如果电路教材这么讲--电容电感计算为什么要引入角频率(ω)而不是直接用频率(f)？

我们在研究电容，电感的时候，频率f是绕不开的参数，可在参与计算的时候角频率ω总是出现在公式中，我们都知道ω=2πf，有时候我就会反问自己，为什么要引入这个角频率呢？就是为了要省掉2πf吗？带着这个疑问我开始今天的话题。

为什么用角频率（ω）而不用普通频率（f）？

频率（f）是 “1秒内转几圈”，而角频率（ω）是 “1秒内跑多远”。

在电容/电感里，ω 直接对应能量变化速度，计算更简单！

——就像车速用“公里/小时”（ω）比“绕操场几圈/小时”（f）更直观一样。

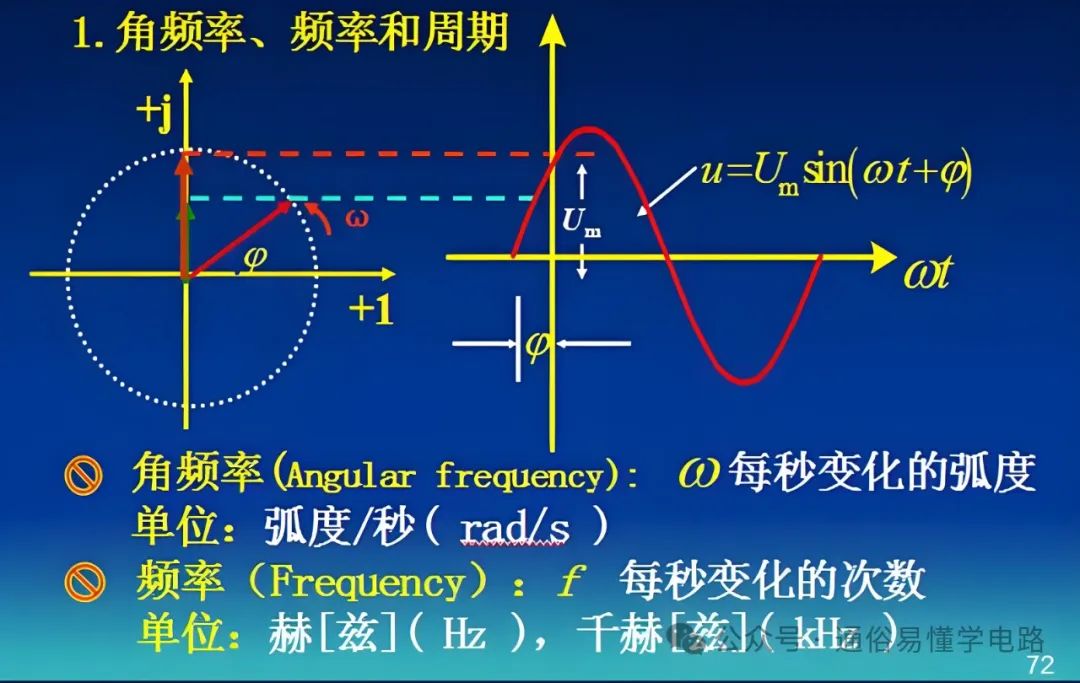
1. 频率（f）和角频率（ω）的区别

	普通频率（f)	角频率(ω)
定义	1秒振动/旋转的次数（单位Hz）	1秒内转过的角度（单位rad/s）
公式	f=1/T（T是周期）	ω=2πf（转一圈=2π弧度）
直观比喻	“发动机每分钟转5000圈”（f=5000 RPM）	“车轮边缘1秒跑了300米”（ω=线性速度）

2. 为什么电容/电感喜欢用ω？

电容和电感的计算涉及“变化率”，而ω直接对应物理量的瞬时变化速度：

1) 电容的电流公式

如果电压是正弦波 

求导后：

→ 电流直接和ω挂钩！用f还得多写一个2π：ω=2πf，麻烦！

(2) 电感的电压公式

同理，电流

 求导后：

→ 电压也直接和ω相关，计算更简洁。

(3) 容抗（Xc）和感抗（XL）

用ω时，公式干净利落。若用f，得写成：

→ 多一堆2π，容易算错！

3. 物理意义：ω是旋转的“真速度”圆周运动

圆周运动中，ω是角速度（比如车轮每秒转多少弧度）。

(电容或电感)的（电压或电流）变化就像旋转的矢量（相量法），用ω描述更自然：

电压或电流的相位差 → 直接用ωt表示角度。

微分或积分→ ω直接乘或除，不用总带着2π。

4. 生活比喻

普通频率（f）：

→ 像说“风扇每分钟转1000圈”，但不知道叶片尖端的实际速度。

角频率（ω）：

→ 像说“风扇叶片尖每秒跑50米”，直接知道能量大小（因为动能和速度相关）。

（电容或电感）就像风扇叶片——研究它们的相互作用时，用ω（速度）比f（圈数）更能反映真实能量变化！

总结

ω的优势：

1.公式更简洁（少写2π）。

2.直接对应电压/电流的变化率。

3.方便描述相位和微分积分运算。

那么什么时候用f呢？

实际测量（如示波器看频率）或日常交流时，用Hz更直观。

一句话：

工程师用ω，是为了少写几个2π，同时让数学更贴近物理本质！ 😎