WC 图论

1.[WC2007]剪刀石头布

题目描述

在一些一对一游戏的比赛（如下棋、乒乓球和羽毛球的单打）中，我们经常会遇到 AA 胜过 BB，BB 胜过 CC 而 CC 又胜过 AA 的有趣情况，不妨形象的称之为剪刀石头布情况。有的时候，无聊的人们会津津乐道于统计有多少这样的剪刀石头布情况发生，即有多少对无序三元组 (A,B,C)(A,B,C)，满足其中的一个人在比赛中赢了另一个人，另一个人赢了第三个人而第三个人又胜过了第一个人。注意这里无序的意思是说三元组中元素的顺序并不重要，将 (A, B, C)(A,B,C)、(A, C, B)(A,C,B)、(B, A, C)(B,A,C)、(B, C, A)(B,C,A)、(C, A, B)(C,A,B) 和 (C, B, A)(C,B,A) 视为相同的情况。

有 NN 个人参加一场这样的游戏的比赛，赛程规定任意两个人之间都要进行一场比赛：这样总共有 \frac{N*(N-1)}{2}2N∗(N−1)​ 场比赛。比赛已经进行了一部分，我们想知道在极端情况下，比赛结束后最多会发生多少剪刀石头布情况。即给出已经发生的比赛结果，而你可以任意安排剩下的比赛的结果，以得到尽量多的剪刀石头布情况。

输入格式

输入文件的第 11 行是一个整数 NN，表示参加比赛的人数。

之后是一个 NN 行 NN 列的数字矩阵：一共 NN 行，每行 NN 列，数字间用空格隔开。

在第 (i+1)(i+1) 行的第 jj 列的数字如果是 11，则表示 ii 在已经发生的比赛中赢了 jj；该数字若是 00，则表示在已经发生的比赛中 ii 败于 jj；该数字是 22，表示 ii 和 jj 之间的比赛尚未发生。数字矩阵对角线上的数字，即第 (i+1)(i+1) 行第 ii 列的数字都是 00，它们仅仅是占位符号，没有任何意义。

输入文件保证合法，不会发生矛盾，当 i \neq ji=j 时，第 (i+1)(i+1) 行第 jj 列和第 (j+1)(j+1) 行第 ii 列的两个数字要么都是 22，要么一个是 00 一个是 11。

输出格式

输出文件的第 11 行是一个整数，表示在你安排的比赛结果中，出现了多少剪刀石头布情况。

输出文件的第 22 行开始有一个和输入文件中格式相同的 NN 行 NN 列的数字矩阵。第 (i+1)(i+1) 行第 jj 个数字描述了 ii 和 jj 之间的比赛结果，11 表示 ii 赢了 jj，00 表示 ii 负于 jj，与输入矩阵不同的是，在这个矩阵中没有表示比赛尚未进行的数字 22；对角线上的数字都是 00。输出矩阵要保证合法，不能发生矛盾。

输入输出样例

输入 #1复制

3
0 1 2
0 0 2
2 2 0

输出 #1复制

1
0 1 0
0 0 1
1 0 0

说明/提示

【评分标准】

对于每个测试点，仅当你的程序的输出第一行的数字和标准答案一致，且给出了一个与之一致的合法方案，你才能得到该测试点的满分，否则该测试点得 00 分。

【数据范围】

30\%30% 的数据中，N \leq 6N≤6；

100\%100% 的数据中，N \leq 100N≤100。

题解：
 

题目大意

竞赛图中的部分边方向已确定，你需要决定剩余边的方向，使得整个图上的三元环数量最多。

题解

从整个图的 nn个点中任取 33个点，方案数为$$C^{3}_{n}=\frac{n!}{3!(n-3)!}=\frac{n(n-1)(n-2)}{6}$$ 考虑 33个点不构成三元环的情况，必然为一点的入度为 22，一点的出度为 22，一点的入度出度为 11。不妨从入度入手，一个点若入度为 22，则表明失去了一个三元环，若入度为 33，则会失去 33个三元环（考虑点 AA被点 B, C, DB,C,D通过边指向，那么 (A,B,C), (A,B,D), (A,C,D)(A,B,C),(A,B,D),(A,C,D)都不会是三元环），因此，对于一个点 uu而言，记其入度为 degree(u)degree(u)，那么点 uu会使整张图会失去 C^{2}_{degree(u)}Cdegree(u)2​个三元环。故对于最终答案 ansans，有

ans = \frac{n(n-1)(n-2)}{6} - \sum_{u \in V}{C^{2}_{degree(u)}}ans=6n(n−1)(n−2)​−u∈V∑​Cdegree(u)2​

通过上述过程已经能够发现，对于一个点 uu，考虑差分，若其入度增加 11，则会使整个图失去的三元环个数为 $$C^{2}{degree(u)} - C^{2}{degree(u)-1} = degree(u)-1$$因此，可以将失去的三元环作费用，跑费用流。

我们对于未定向的边，将其视为点（以下称作「边对应的点」），建图如下：

1.1. 由源点 ss向每一条边对应的点连边，容量为 11，费用为 00；

2.2. 由每一条边对应的点向该边连接的两个图上结点连边，容量为 11，费用为 00，表明该条边只会使得其中一个点入度 +1+1；

3.3. 由每一个图上结点向汇点 tt连若干条边，费用依次为 0, 1, 2, 3......0,1,2,3......（分别表示该点入度从 00开始每增加 11就会失去的三元环数量），容量均为 11（注意初始图的处理，即某些点初始入度不为 00）。

最后的输出方案，对于未定向边，只需看费用流的图中，边对应的点指向的两个图上结点的边中哪一条满流即可。

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;

const int maxn = 5150 + 10;
const int maxg = 100 + 10;
const int INF = 1000000000;

int n;
int s, t;
int rel[maxg][maxg];
int wedge[maxg][maxg];
int indeg[maxn];

int edgeidx(int x, int y) {
  return (2*n-x) * (x-1) / 2 + (y-x) + n;
}

struct Edge {
  int from, to, cap, flow, cost;
  Edge(int from, int to, int cap, int flow, int cost):
    from(from), to(to), cap(cap), flow(flow), cost(cost) {}
};

template <int maxn> struct MCMF {
  int n, m, s, t;
  vector <Edge> edges;
  vector <int> G[maxn];
  int inq[maxn];
  int d[maxn];
  int p[maxn];
  int a[maxn];

  void init(int n) {
    this->n = n;
    for(int i = 0; i < n; i++) G[i].clear();
    edges.clear();
  }

  void AddEdge(int from, int to, int cap, int cost) {
    edges.push_back(Edge(from, to, cap, 0, cost));
    edges.push_back(Edge(to, from, 0, 0, -cost));
    m = edges.size();
    G[from].push_back(m-2);
    G[to].push_back(m-1);
  }

  bool BellmanFord(int s, int t, int& cost) {
    for(int i = 0; i < n; i++) d[i] = INF;
    memset(inq, 0, sizeof(inq));
    d[s] = 0; inq[s] = 1; p[s] = 0; a[s] = INF;
  
    queue <int> Q;
    Q.push(s);
    while(!Q.empty()) {
      int u = Q.front(); Q.pop();
      inq[u] = 0;
      for(int i = 0; i < G[u].size(); i++) {
        Edge& e = edges[G[u][i]];
        if(e.cap > e.flow && d[e.to] > d[u] + e.cost) {
          d[e.to] = d[u] + e.cost;
          p[e.to] = G[u][i];
          a[e.to] = min(a[u], e.cap - e.flow);
          if(!inq[e.to]) { Q.push(e.to); inq[e.to] = 1; }
        }
      }
    }
    if(d[t] == INF) return false;
    cost += d[t] * a[t];
    int u = t;
    while(u != s) {
      edges[p[u]].flow += a[t];
      edges[p[u]^1].flow -= a[t];
      u = edges[p[u]].from;      
    }
    return true;
  }

  int Mincost(int s, int t) {
    int cost = 0;
    while(BellmanFord(s, t, cost));
    return cost;
  }
};
  
MCMF <maxn> solver;
  
int main() {
  scanf("%d", &n);
  s = 0; t = (n+1)*n/2 + n + 1;
  solver.init(t+1);
  for(int i = 1; i <= n; i++)
    for(int j = 1; j <= n; j++) {
      scanf("%d", &rel[i][j]);
      if(rel[i][j] == 1) indeg[j]++;
    }

  for(int i = 1; i <= n; i++)
    for(int j = i+1; j <= n; j++) {
      if(rel[i][j] < 2) continue;
      solver.AddEdge(s, edgeidx(i, j), 1, 0);
      solver.AddEdge(edgeidx(i, j), i, 1, 0);
      wedge[j][i] = solver.m - 2;
      solver.AddEdge(edgeidx(i, j), j, 1, 0);
      wedge[i][j] = solver.m - 2;
    }

  int down = 0;
  for(int i = 1; i <= n; i++) {
    down += indeg[i] * (indeg[i]-1) / 2;
    for(int j = indeg[i] + 1; j < n; j++)
      solver.AddEdge(i, t, 1, j-1);
  }

  down += solver.Mincost(s, t);

  printf("%d\n", n*(n-1)*(n-2) / 6 - down);

  for(int i = 1; i <= n; i++) {
    for(int j = 1; j <= n; j++) {
      if(rel[i][j] < 2) printf("%d", rel[i][j]);
      else printf("%d", solver.edges[wedge[i][j]].flow);
      if(j < n) printf(" ");
    }
    printf("\n");
  }

  return 0;
}

2. [WC2016]挑战NPC

题目描述

小 N 最近在研究 NP 完全问题，小 O 看小 N 研究得热火朝天，便给他出了一道这样的题目：

有 nn 个球，用整数 11 到 nn 编号。还有 mm 个筐子，用整数 11 到 mm 编号。每个筐子最多能装 33 个球。

每个球只能放进特定的筐子中。 具体有 ee 个条件，第 ii 个条件用两个整数 v_ivi​ 和 u_iui​ 描述，表示编号为 v_ivi​ 的球可以放进编号为 u_iui​ 的筐子中。

每个球都必须放进一个筐子中。如果一个筐子内有不超过 11 个球，那么我们称这样的筐子为半空的。

求半空的筐子最多有多少个，以及在最优方案中， 每个球分别放在哪个筐子中。

小 N 看到题目后瞬间没了思路，站在旁边看热闹的小 I 嘿嘿一笑：“水题！” 然后三言两语道出了一个多项式算法。

小 N 瞬间就惊呆了，三秒钟后他回过神来一拍桌子：“不对！这个问题显然是 NP 完全问题，你算法肯定有错！”

小 I 浅笑：“所以，等我领图灵奖吧！”

小 O 只会出题不会做题，所以找到了你——请你对这个问题进行探究，并写一个程序解决此题。

输入格式

输入文件 \tt{npc.in}npc.in 第一行包含 11 个正整数 TT， 表示有 TT 组数据。

对于每组数据，第一行包含 33 个正整数 n, m, en,m,e， 表示球的个数，筐子的个数和条件的个数。

接下来 ee 行，每行包含 22 个整数 v_i, u_ivi​,ui​， 表示编号为 v_ivi​ 的球可以放进编号为 u_iui​ 的筐子。

输出格式

输出文件为 \tt{npc.out}npc.out。

对于每组数据，先输出一行，包含一个整数，表示半空的筐子最多有多少个。

然后再输出一行，包含 nn 个整数 p_1, p_2, ... , p_np1​,p2​,...,pn​，相邻整数之间用空格隔开，表示一种最优解。其中 p_ipi​ 表示编号为 ii 的球放进了编号为 p_ipi​ 的筐子。 如果有多种最优解，可以输出其中任何一种。

输入输出样例

输入 #1复制

1
4 3 6
1 1
2 1
2 2
3 2
3 3
4 3

输出 #1复制

2
1 2 3 3

说明/提示

对于所有数据， T \leq 5, 1 \leq n \leq 3mT≤5,1≤n≤3m。 保证 1 \leq v_i \leq n, 1 \leq u_i \leq m1≤vi​≤n,1≤ui​≤m，且不会出现重复的条件。

保证至少有一种合法方案，使得每个球都放进了筐子，且每个筐子内球的个 数不超过 33。

各测试点满足以下约定： 

 

 

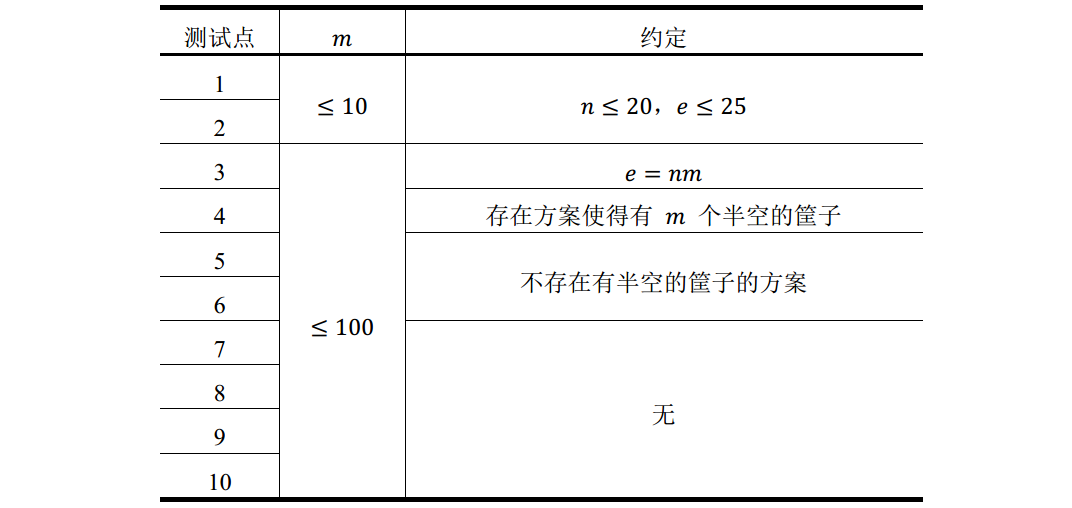
题解：

solution :

在 WC2021 Day 1 晚上听了“调整算法”，感觉很神仙，而校内 OJ 只有一道一般图最大匹配的题，于是就写了一下。

建图的方法这里就不多说了，其他题解都有，就是把一个筐子拆成三个点然后互相连边。

至于”调整算法“就是记录一个一开始为空的匹配，每一次随机一个没有匹配的点并枚举出边，如果也有没有匹配的点就匹配上并ans++，否则随机一个点拆掉原来的匹配并与现在的点匹配。

我是进行了4e5次上述的操作，这样就可以得出最大匹配的大小了（darkbzoj）,但这样求出的方案不一定 1~n 都是匹配点，所以我想出了一种奇怪的做法，就是每次随机点的时候如果有未匹配的1~n的点就优先选，然后莫名其妙就对了（

然后好像在所有OJ都是最慢解

code :

#include <bits/stdc++.h>
using namespace std;
int T, n, m, e, vis_num, num, head[1000000], nxt[1000000], to[1000000], cnt,
    vis[1000000], v[1000000], out[1000000], i;
void add(int a, int b) { nxt[++cnt] = head[a], to[cnt] = b, head[a] = cnt; }
void link(int a, int b) {
  vis[vis[a]] = vis[vis[b]] = 0, vis[a] = b, vis[b] = a;
}
int main() {
  cin >> T;
  while (T--) {
    cnt = vis_num = 0;
    memset(vis, 0, sizeof(vis));
    memset(head, 0, sizeof(head));
    memset(out, 0, sizeof(out));
    cin >> n >> m >> e;
    for (int i = 1; i <= e; i++) {
      int u, v;
      cin >> u >> v;
      int s = n + (v - 1) * 3;
      add(s + 2, u), add(u, s + 3), add(s + 3, u), add(u, s + 2), add(u, s + 1),
          add(s + 1, u);
    }
    for (int i = 1; i <= m; i++) {
      int s = n + (i - 1) * 3;
      add(s + 2, s + 3), add(s + 3, s + 2), add(s + 1, s + 2),
          add(s + 3, s + 1), add(s + 2, s + 1), add(s + 1, s + 3);
    }
    int tot = n + m * 3, ans = 0, _ = 1;
    while (++_ <= 200000 || !out[1]) {
      for (num = 0, i = 1; i <= tot; i++)
        if (!vis[i]) v[++num] = i;
      if (!num) break;
      int now = v[1] <= n ? v[1] : v[rand() % num + 1];
      vis_num += now <= n, num = 0;
      for (i = head[now]; i; i = nxt[i]) {
        if (!vis[to[i]]) {
          ans++;
          link(now, to[i]);
          if (to[i] <= n) vis_num++;
          goto ed;
        } else
          v[++num] = to[i];
      }
      {
        int to = v[rand() % num + 1];
        vis_num -= (vis[to] <= n);
        link(now, to);
      }
    ed:
      if (vis_num == n) memcpy(out, vis, sizeof(int) * (tot + 1));
    }
    cout << ans - n << endl;
    for (i = 1; i <= n; i++) {
      cout << (out[i] - n - 1) / 3 + 1 << " ";
    }
    cout << endl;
  }
  return 0;
}

 

3. [WC2011]最大XOR和路径

题目描述

XOR（异或）是一种二元逻辑运算，其运算结果当且仅当两个输入的布尔值不相等时才为真，否则为假。 XOR 运算的真值表如下（11 表示真， 00 表示假）：

输入	输入	输出
A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

而两个非负整数的 XOR 是指将它们表示成二进制数，再在对应的二进制位进行 XOR 运算。

譬如 1212 XOR 99 的计算过程如下：

12=(1100)_2\ \ \ 9=(1001)_2\\ \begin{matrix} &1\ 1\ 0\ 0\\ \text{XOR}&1\ 0\ 0\ 1\\ \hline &0\ 1\ 0\ 1\\ \end{matrix}\\ (0101)_2=512=(1100)2​   9=(1001)2​XOR​1 1 0 01 0 0 10 1 0 1​​(0101)2​=5

故 1212 XOR 9 = 59=5。

容易验证， XOR 运算满足交换律与结合律，故计算若干个数的 XOR 时，不同的计算顺序不会对运算结果造成影响。从而，可以定义 KK 个非负整数 A_1A1​，A_2A2​，……，A_{K-1}AK−1​，A_KAK​的 XOR 和为

A_1A1​ XOR A_2A2​ XOR …… XOR A_{K-1}AK−1​ XOR A_KAK​

考虑一个边权为非负整数的无向连通图，节点编号为 11 到 NN，试求出一条从 11 号节点到 NN 号节点的路径，使得路径上经过的边的权值的 XOR 和最大。

路径可以重复经过某些点或边，当一条边在路径中出现了多次时，其权值在计算 XOR 和时也要被计算相应多的次数，具体见样例。

输入格式

输入文件 xor.in 的第一行包含两个整数 NN 和 MM， 表示该无向图中点的数目与边的数目。

接下来 MM 行描述 MM 条边，每行三个整数 S_iSi​， T_iTi​ ， D_iDi​， 表示 S_iSi​ 与 T_iTi​ 之间存在一条权值为 D_iDi​ 的无向边。

图中可能有重边或自环。

输出格式

输出文件 xor.out 仅包含一个整数，表示最大的 XOR 和（十进制结果）。

输入输出样例

输入 #1复制

5 7
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2

输出 #1复制

6

说明/提示

【样例说明】

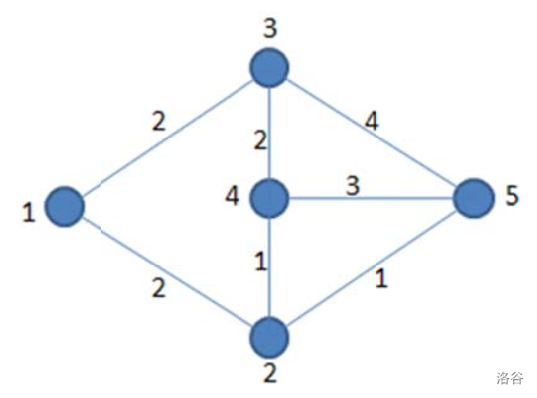
如图，路径1 \rightarrow 2 \rightarrow 4 \rightarrow 3 \rightarrow 5 \rightarrow 2 \rightarrow 4 \rightarrow 51→2→4→3→5→2→4→5对应的XOR和为

22 XOR 11 XOR 22 XOR 44 XOR 11 XOR 11 XOR 3 = 63=6

当然，一条边数更少的路径1 \rightarrow 3 \rightarrow 51→3→5对应的XOR和也是22 XOR 4 = 64=6。

【数据规模】

对于 20 \%20% 的数据，N \leq 100N≤100， M \leq 1000M≤1000，D_i \leq 10^{4}Di​≤104；

对于 50 \%50% 的数据，N \leq 1000N≤1000， M \leq 10000M≤10000，D_i \leq 10^{18}Di​≤1018；

对于 70 \%70% 的数据，N \leq 5000N≤5000， M \leq 50000M≤50000，D_i \leq 10^{18}Di​≤1018；

对于 100 \%100% 的数据，N \leq 50000N≤50000， M \leq 100000M≤100000，D_i \leq 10^{18}Di​≤1018。

题解：

题目要求很多条边的最大异或和，从这一点我们可以想到线性基。这里归纳一下线性基的几点性质：

设VV是某个神奇的向量空间，BB是VV的基，则BB应满足以下条件：

1.VV是BB的极小生成集，就是说只有BB能张成VV，而它的任何真子集都不张成全部的向量空间。

2.BB是VV中线性无关向量的极大集合，就是说BB在VV中是线性无关集合，而且VV中没有其他线性无关集合包含它作为真子集。

3.VV中所有的向量都可以按唯一的方式表达为BB中向量的线性组合。

这也就是说，我们可以用不超过log_{2}{m}log2​m个基就能表示所有的异或和，考虑题目中一句重要的话：

路径可以重复经过某些点或边，当一条边在路径中出现了多次时，其权值在计算 XOR 和时也要被计算相应多的次数

这句话给了我们一点启发，假设某条路kk被重复走了两次，那么它的权值对答案的贡献就是00，但是通过这条路径kk，我们可以到达它连接的另一个点。

显然我们没法枚举11~NN的每一条路，但我们可以将路径拆成两部分，第一部分是环，第二部分是链。

于是我们枚举所有环，将环上异或和扔进线性基，然后用这条链作为初值，求线性基与这条链的最大异或和。

void dfs(int u,LL res) {//枚举所有环
    del[u]=res,vis[u]=1;
    for (int i=head[u];i;i=e[i].next)
        if (!vis[e[i].to]) dfs(e[i].to,res^e[i].w);
        else insert(res^e[i].w^del[e[i].to]);
}
LL query(LL x) {//最大异或和
    LL res=x;
    for (int i=63;i>=0;i--)
        if ((res^num[i])>res)
            res^=num[i];
    return res;
}

这道题的算法是：找出所有环，扔进线性基，随便找一条链，以它作为初值求最大异或和就可以了。

附上AC代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define LL long long
LL num[70];
bool insert(LL x) {
    for (int i=63;i>=0;i--)
        if ((x>>i)&1) {
            if (!num[i]) {
                num[i]=x;
                return true;
            }
            x^=num[i];
        }
    return false;
}
LL query(LL x) {
    LL res=x;
    for (int i=63;i>=0;i--)
        if ((res^num[i])>res)
            res^=num[i];
    return res;
}
struct edge {
    int to,next;
    LL w;
}e[200010];
int head[50010],ecnt;
inline void adde(int from,int to,LL w) {
    e[++ecnt]=(edge){to,head[from],w},head[from]=ecnt;
    e[++ecnt]=(edge){from,head[to],w},head[to]=ecnt;
}
int vis[50010];LL del[50010];
void dfs(int u,LL res) {
    del[u]=res,vis[u]=1;
    for (int i=head[u];i;i=e[i].next)
        if (!vis[e[i].to]) dfs(e[i].to,res^e[i].w);
        else insert(res^e[i].w^del[e[i].to]);
}
int main() {
    int n,m,a,b;LL c;scanf("%d%d",&n,&m);
    for (int i=1;i<=m;i++) scanf("%d%d%lld",&a,&b,&c),adde(a,b,c);
    dfs(1,0);
    printf("%lld\n",query(del[n]));
}